RELACION CUERDAS Y BUCLES

La teoría de la relatividad general cambió para siempre nuestra
forma de ver el Universo que nos rodea: el espacio y el tiempo son parte de una
entidad 4-dimensional dinámica denominada espacio-tiempo. Sin embargo, en la
teoría relativista el espacio-tiempo está definido de forma clásica y es sabido
que a nivel fundamental la naturaleza es cuántica. Por esto, el espacio-tiempo
debe emerger a partir de constituyentes fundamentales a escala cuántica.
Entender cuáles son estos constituyentes y como emerge el espacio-tiempo es una
de las tareas más fundamentales y trascendentes de la historia de la física y
del conocimiento humano. En este artículo veremos tres aproximaciones a este
formidable reto: dos desde el punto de vista de la teoría de cuerdas y una
desde el punto de vista de la gravedad cuántica de bucles. Además explicaremos
una fascinante relación entre ambas teorías que podría conducir a una
unificación de nuestras dos principales aproximaciones de gravedad cuántica.
Bienvenidos al estudio de la naturaleza fundamental del
espacio-tiempo.
La
emergencia del espacio-tiempo clásico en teoría de cuerdas
En una primera aproximación afrontaremos la emergencia del
espacio-tiempo clásico de la relatividad general en teoría de cuerdas. En
teoría de cuerdas la noción de espacio-tiempo está ligada a un objeto
denominado "hoja de mundo" (world sheet) que describe el movimiento
de las cuerdas en el espacio-tiempo. Este movimiento describe una hoja
bidimensional:
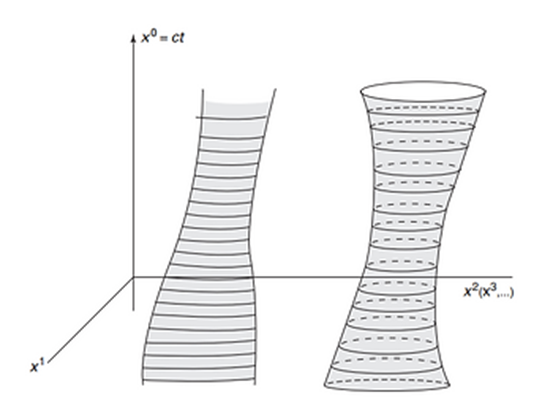
Superficie (worldsheet) formada por el movimiento de una cuerda
abierta (izquierda) y una cuerda cerrada (derecha).
El movimiento de las cuerdas formando la "worldsheet"
está descrito por los denominados "modelos sigma". Estos modelos
tienen la peculiaridad de que el acoplamiento g que determina la fuerza de la
interacción no es constante sino que depende del campo gravitatorio. El estudio
de estos modelos nos indica que solo son consistentes si poseen una simetría
especial denominada "simetría de Weyl" y esta simetría solo se
manifiesta si los campos son invariantes ante cambios de coordenadas es decir, si
cumplen con las ecuaciones de la relatividad general. Este
hecho nos permite vislumbrar la emergencia del espacio-tiempo clásico en teoría
de cuerdas:
las cuerdas solo pueden residir en hojas de mundo cuyos campos
cumplen con las ecuaciones de la relatividad general. Este impresionante
resultado llevo al físico David Tong a escribir:
"That tiny string is seriously high-maintenance: its
requirements are so stringent that they govern the way the whole universe
moves"
"Esa pequeña cuerda requiere un gran mantenimiento: sus
requisitos son tan estrictos que gobiernan la forma en que se mueve todo el
Universo"
La
emergencia del espacio-tiempo cuántico en teoría de cuerdas
El cuanto de la interacción gravitatoria es el gravitón. A
continuación analizaremos que le sucede a la acción de la world-sheet cuando se
produce una interacción con un gravitón. La acción asociada a la cuerda en la
worldsheet viene dada por:
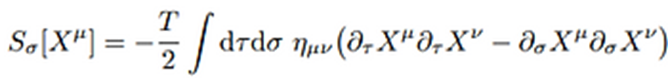
El gravitón está descrito por un tensor simétrico sin traza S. Para analizar
este proceso a nivel cuántico usaremos la integral de caminos de Feynman cuyo
valor depende del factor eiS(x). Si perturbamos esta métrica incluyendo una
interacción con un gravitón tenemos:
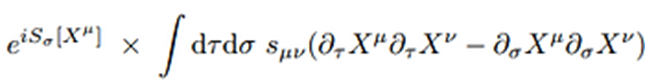
En teoría de campos la aparición de campos clásicos se produce a través de
"estados coherentes", es decir, a través de una superposición de un
gran número de estados excitados. Este hecho, nos hace vislumbrar la emergencia
del espacio-tiempo a nivel cuántico: este parece emerger del entrelazamiento
de muchos estados cuánticos.
Si consideramos un número muy grande n de estados entonces la
interacción viene dada por:
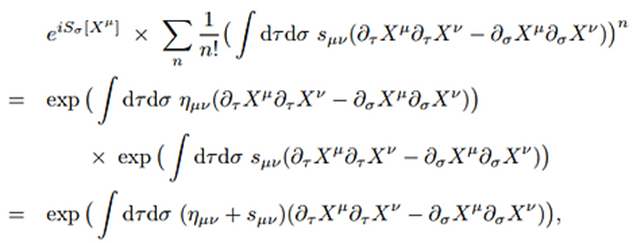
Pero esta amplitud es exactamente la que obtendríamos si hubiésemos modificado
nuestra métrica original de la forma:
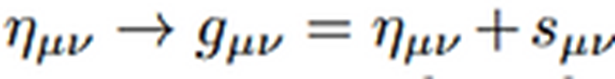
Esto quiere decir que, en lo que respecta a la integral de caminos, no existe
diferencia entre un espacio-tiempo curvo y un espacio-tiempo plano de Minkowsky
con una excitación coherente de gravitones. Esto nos indica que la curvatura
del espacio-tiempo es producido por un estado coherente de gravitones.
Emergencia
del espacio-tiempo y holografía
Antes de empezar este apartado debemos revisar dos conceptos clave
sobre los dos objetos básicos de la teoría de cuerdas: las cuerdas y las
D-branas.
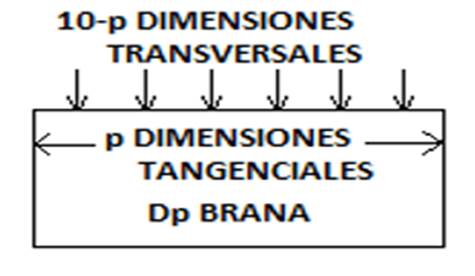
1º) Una Dp-brana es un objeto de p dimensiones con cuerdas abiertas
adheridas a su superficie. Este objeto separa las 10 dimensiones totales del
espacio-tiempo en dos grupos: p dimensiones tangentes a la Dp-brana y 10-p
dimensiones transversales (perpendiculares) a la Dp-brana.
2º) Las cuerdas abiertas poseen cargas eléctricas en sus extremos. Como estos
extremos están adheridos a las D-branas las branas portan carga eléctrica (en
realidad portan un campo equivalente denominado campo de Kalb-Ramond). De forma
similar a como el campo eléctrico posee simetría U(1), N cuerdas adheridas a la
D-brana producen una simetría SU(N).
A continuación ya estamos en situación de explicar la emergencia
del espacio-tiempo en el contexto de la holografía. Como es sabido, la teoría
de supercuerdas se basa en un espacio-tiempo de 10 dimensiones. Imaginar que
tenemos un número muy grande N de 3D-branas apiladas en una misma región del
espacio-tiempo. El acoplamiento g describe la fuerza de la interacción entre
cuerdas. Veremos que sucede según variamos este parámetro desde un valor muy
pequeño hasta un valor muy grande.
Escenario
para g muy pequeño
Cuando el acoplamiento es muy pequeño tenemos dos sistemas físicos
completamente desacoplados: el conjunto de D3-branas apiladas y un conjunto de
cuerdas cerradas (el campo gravitatorio) que se propagan libremente por las 10
dimensiones del espacio-tiempo:
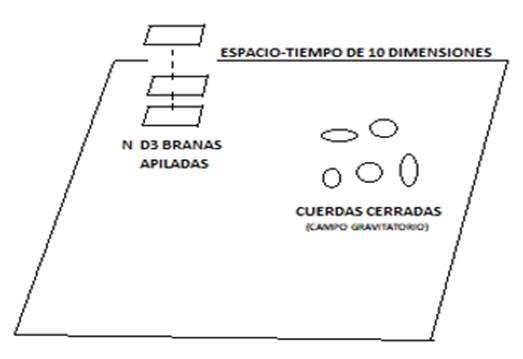
Como vimos al principio de este apartado un conjunto de N D-branas coincidentes
producen un sistema con simetría SU(N). Por tanto, el primer sistema consiste
en una teoría gauge supersimétrica con simetría SU(N) y el segundo sistema
consiste en una teoría de cuerdas cerradas denominada teoría de supercuerdas
tipo IIA.
Este escenario se traduce en un conjunto de N de 3D-branas en un
espacio-tiempo plano de 10 dimensiones. La distribución de estas dimensiones es
la siguiente:
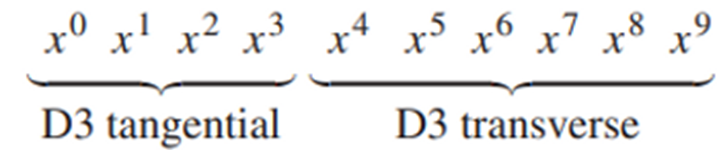
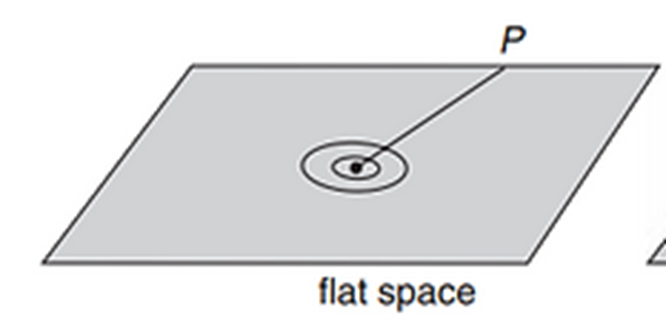
Imaginemos un observador en una nave espacial en este espacio-tiempo. La nave
se dirige hacia el punto P y va midiendo el tamaño de los círculos concéntricos
alrededor de este punto. Según nos acercamos a P la longitud de estos círculos
va disminuyendo progresivamente hasta alcanzar longitud cero justo al alcanzar
el punto P:
Escenario para g muy grande
Según aumentamos el valor del acoplamiento y llegamos a un valor
donde g>>1 los efectos gravitatorios comienzan a ser importantes y las
D3-branas comienzan a interactuar. Estas branas portan masa, energía y el
equivalente a un campo eléctrico:
el denominado campo de Kalb-Ramond. Como la energía sigue siendo
baja comparada con la energía natural de las cuerdas (1/ls donde ls es la
longitud de la cuerda) podemos utilizar las soluciones de baja energía de la
teoría de supercuerdas.
La solución tiene una métrica de la forma siguiente:
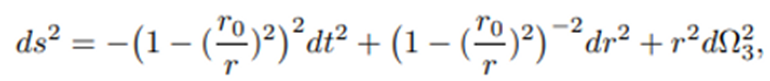
Esta solución representa un espacio-tiempo con la siguiente geometría:
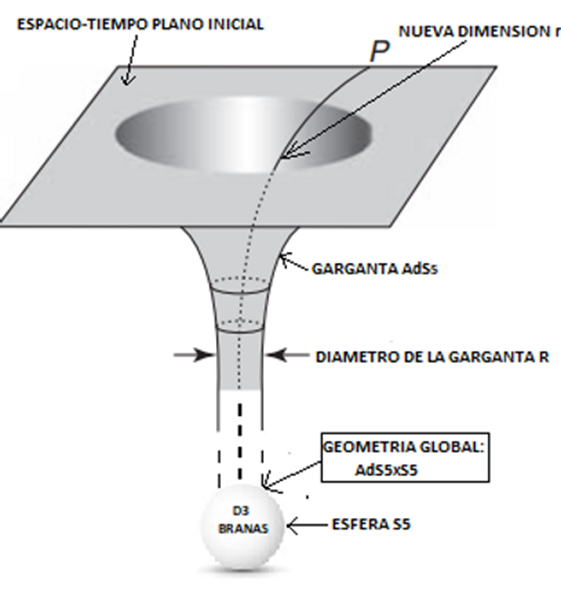
Ahora la geometría en torno a P ha cambiado radicalmente. ¡El punto P ha sido
desplazado a una infinita distancia respecto a cualquier otro punto del
espacio-tiempo!
En esta geometría nuestra nave de exploración detectará que según
se acerca al punto P el tamaño de los círculos concéntricos va disminuyendo y
se va acercando de forma asintótica a un valor fijo R. Este valor es el radio
de la garganta de longitud infinita.
La nueva distribución de las dimensiones espacio-temporales es la
siguiente:
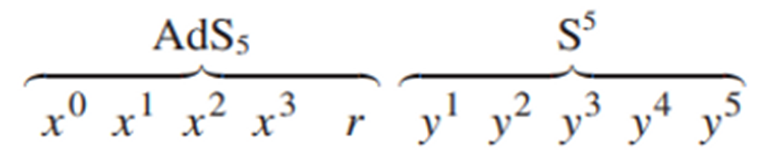
La garganta junto con el espacio-tiempo hiperbólico que se "pega" asintóticamente
al espacio-tiempo plano representa una geometría AdS5. Al final de la infinita
garganta tenemos una esfera de 5 dimensiones. Por tanto el espacio-tiempo
global en el fondo de la garganta tiene una simetría AdS5xS5.
El punto clave es que se ha producido una redistribución de las
dimensiones espaciales originales. Inicialmente tenemos un conjunto de
D3-branas ocupando un espacio de 3 dimensiones más 1 dimensión temporal, esto
nos deja un total de 6 dimensiones transversales a las branas. Al aumentar el
acoplamiento cinco de las dimensiones transversales se transforman en una
5-esfera y las 3 dimensiones de las branas más la dimensión temporal forman la
"garganta" del espacio AdS. Pero entonces ¿Qué ha sucedido con la dimensión
transversal que nos falta? La respuesta es que esta dimensión también ha pasado
a formar parte del espacio AdS de la garganta. Si nos fijamos la garganta posee
una nueva dimensión: la dimensión r. Podemos afirmar que de alguna forma esta dimensión
es emergente. De forma esquemática la redistribución sería la siguiente:
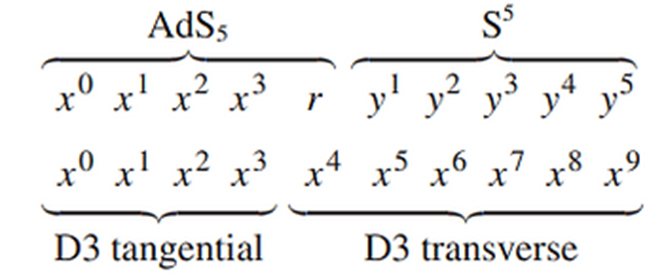
Redistribución de las dimensiones originales al aumentar el
acoplamiento: las 3+1 dimensiones de las 3-branas más una dimensión r
transversal se transforman en un espacio AdS5, las otras 5 dimensiones
transversales a las 3-branas forman una 5-esfera.
Todo este proceso implica lo siguiente: a bajo acoplamiento tenemos dos
sistemas desconectados: una teoría gauge SU(N) y una teoría de supercuerdas
tipo IIA. A alto acoplamiento tenemos una geometría AdS5xS5. La conclusión que
podemos sacar de este escenario es que la teoría gauge y la geometría AdS5xS5
son en realidad ¡la misma teoría! Esta es la famosa dualidad AdS/CFT:
una teoría conforme formulada en N dimensiones es equivalente a una geometría
AdS formulada en N+1 dimensiones.
La dualidad AdS/CFT tiene similitudes con la física de un sistema
de información holográfico: toda la información de una imagen 3D puede
almacenarse en una imagen holográfica 2D. De esta forma el sistema CFT almacena
toda la información sobre la geometría AdS y decimos que el espacio-tiempo AdS surge
de forma holográfica.
La
emergencia del espacio-tiempo en Teoría Cuántica de Bucles
Uno de los principios básicos de la Teoría Cuántica de Bucles
(LQG) es que todas las magnitudes que describen la geometría (longitudes,
áreas, etc.) están cuantizadas. Esto es debido a que el espacio-tiempo a nivel
fundamental es discreto debido a la existencia de un tamaño mínimo: la longitud
de Planck. Por esto, si tomamos un volumen de espacio cualquiera, por ejemplo,
un tetraedro, todas las medidas que podamos realizar sobre el estarán
cuantizadas. Para describir el tetraedro debemos tomar las variables
independientes más adecuadas. En LQG el vínculo entre mecánica cuántica y
geometría tiene su origen en el simple producto vectorial de dos vectores:
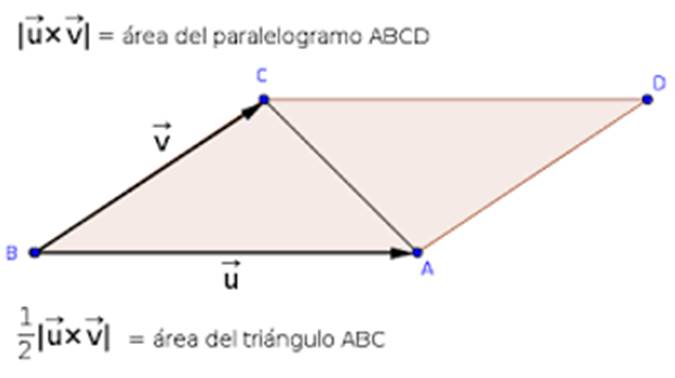
De esta forma en LQG las caras del tetraedro se describen como la superficie
determinada por 1/2 del producto vectorial de los 2 lados que forman el
triángulo.
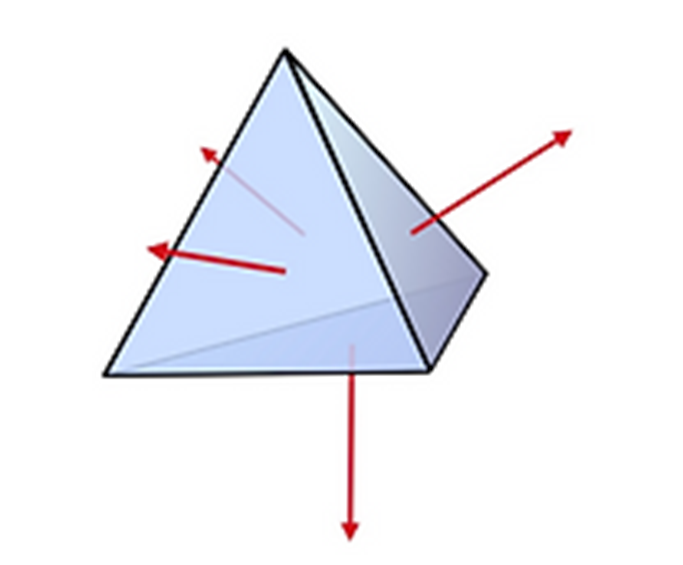
Este producto vectorial define cuatro vectores (Lo,L1,L2,L3) perpendiculares a
las cuatro caras. Estos vectores poseen toda la información sobre la geometría
del tetraedro. Por ejemplo la superficie de las caras viene dada por el módulo
del vector L y el volumen del tetraedro viene dado por:
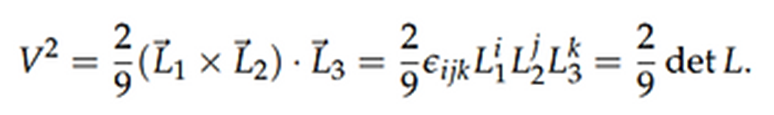
Además, debido a la simetría rotacional la suma de los cuatro vectores es cero:
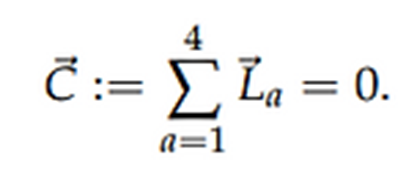
Debido a esta simetría rotacional los valores de los cuatro vectores forman un
grupo: el grupo SU(2). ¡Este es el grupo que determina el spin, es decir, el
momento angular!
Este es el vínculo que buscábamos entre geometría (espacio-tiempo)
y mecánica cuántica: puesto que los vectores L que describen al tetraedro
representan valores de momento angular y estos valores tienen que estar
cuantizados en LQG podemos usar los valores cuantizados asociados al spin
cuántico. Estos valores vienen dados por las representaciones del grupo SU(2).
Por tanto, los valores cuantizados del área vienen dados por:
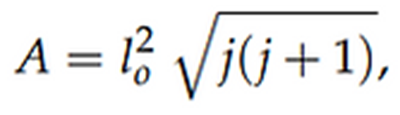
Donde lo es una constante con unidades de área. Por ello tenemos que a cada
valor del momento angular j le corresponde un valor de una superficie S. Esta
es la forma en la que el espacio-tiempo "emerge" en LQG.
Hacia
una relación entre la Teoría de Cuerdas y la Teoría Cuántica de Bucles
Los apartados anteriores basados en teoría de cuerdas (TC) ponen
de manifiesto una carencia muy importante: la teoría parte inicialmente de un
espacio-tiempo preexistente en el que se mueven las cuerdas que generan la
worldsheet. Por esto se dice que la teoría de cuerdas no es independiente del
entorno. La teoría cuántica de la gravedad definitiva debería ser capaz de
explicar cómo emerge el espacio-tiempo de componentes cuánticos fundamentales.
La teoría cuántica de bucles (LQG) es capaz de solucionar esa carencia ya que
no parte de un espacio-tiempo inicial sino que el espacio-tiempo surge a partir
de una estructura pre-geométrica definida por la teoría. Sin embargo, LQG tiene
otra carencia fundamental: no está claro como emerge el espacio-tiempo clásico
de la relatividad general a partir de la estructura pre-geométrica de la
teoría. Por ello algunos físicos han propuesto un posible vínculo entre ambas
teorías: LQG aportaría la estructura pre-geométrica del espacio-tiempo mientras
que la TC representa la teoría efectiva que describe la dinámica de
esa estructura pre-geométrica y que da lugar al espacio-tiempo que observamos.
A continuación explicaré brevemente esta posible y fascinante relación.
Los valores de j permitidos por LQG son plasmados en un grafo del
tipo:
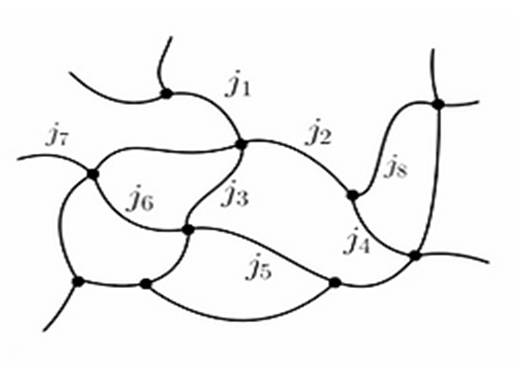
Dada una superficie S definida en un grafo de LQG podemos calcular el valor del
área total de la forma siguiente: dividimos el área total en un número I muy
grande de unidades de área. El área de estas unidades será:
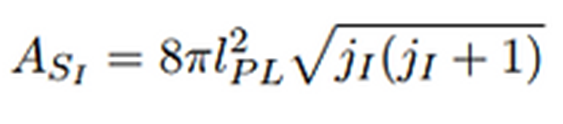
Donde ji es la representación de SU(2) asignada a la i-enésima celda de la
superficie.
El punto clave relevante en nuestra discusión es que una vez
definida una superficie en un grafo de LQG esta puede expresarse como una suma
de "unidades fundamentales de área". Esta suma se realiza contando
todos los puentes del grafo que atraviesan la superficie total que hemos
definido. La unidad fundamental de área se expresa en función del momento
angular j que es un estado del grupo SU(2), esto es, un valor de spin:
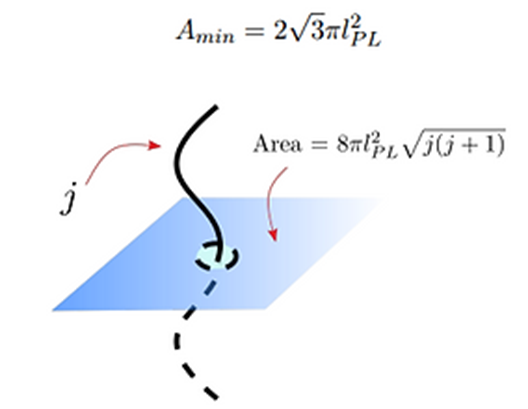
Representación de un único puente de un grafo de LQG: el puente del
grafo "pincha" la superficie y define una unidad de área. De esta
forma el área es expresado en función del momento angular j de la
representación de SU(2). (El mínimo valor posible de área se obtiene
sustituyendo j por 1/2 que es el mínimo valor de j, ver primera expresión).
Fijémonos ahora en cómo se define el
área en teoría de cuerdas. En TC la acción de la worldsheet viene dada por la
denominada acción de Nambu-Goto:
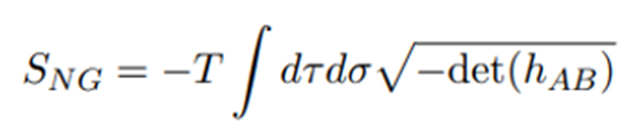
Donde la raíz cuadrada de hAB es precisamente el área de la worldsheet. Para
derivar la dinámica debemos calcular el extremo mínimo de la acción (principio
de mínima acción).
A continuación nos hacemos la pregunta clave: suponiendo que no
existe un espacio-tiempo preexistente y por tanto no podemos medir longitudes
ni áreas ¿Como podríamos definir el objeto hAB en la acción de Nambu-Goto?
Resulta que LQG tiene la respuesta a esta pregunta crucial. Supongamos que
tenemos un gran número de cuerdas moviéndose en una pre-geometría sin ninguna
estructura, sin ninguna métrica definida. Las worldsheet de cada una de las
cuerdas se interceptarán mutuamente un gran número de veces. Siguiendo los
principios de LQG a cada uno de esos puntos de intersección le podemos asignar
una unidad de área cuyo valor viene dado por el momento angular j de la cuerda
que intersecta la worldsheet. De esta forma el área total de la worldsheet será
el valor esperado (la media estadística) de todas estas unidades de
área:
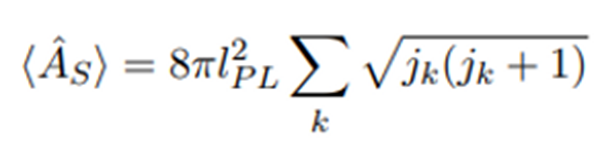
Puesto que las cuerdas portan masa y energía, para un número muy grande de
ellas uno espera que la tendencia sea evitar que las cuerdas se solapen es
decir minimizar el número de choques entre cuerdas. Esto equivale a minimizar
el valor esperado del operador de área. Pero realizar esta operación equivale
precisamente a minimizar el área y la acción de Nambu-Goto. Por tanto
concluimos que la acción de Nambu-Goto surge debido a la necesidad de
minimizar el valor esperado del operador de área de LQG. ¡Esta es la
sorprendente relación entre la teoría de cuerdas y la gravedad cuántica de
bucles!
Esta relación podría suponer la unificación de ambas teorías, lo
que supondría un enorme paso hacia la teoría de gravedad cuántica final.
© 2024 JAVIER DE LUCAS