DENTRO DE UN AGUJERO NEGRO

¿Cómo podemos siquiera intentar describir lo que sucede en el interior de un agujero negro? Aunque parezca increíble, podemos utilizar ciertos aspectos generales de la teoría de cuerdas para tratar de vislumbrar la estructura interior fundamental de estos extraños objetos.

En este artículo nos adentraremos en el interior de los agujeros negros y descubriremos algunos aspectos de sus "componentes interiores fundamentales". Estos componentes podrían ser la clave del problema más profundo de la física fundamental: establecer la naturaleza primordial del propio espacio-tiempo.

Dimensiones compactadas y estados de Kaluza-Klein

El modelo estándar de la física de partículas explica todas las fuerzas fundamentales excepto la gravedad y está basado en los denominados campos gauge. Como vimos en un artículo anterior, los físicos Teodor Kaluza y Felix Klein (KK) descubrieron que el campo de fuerza electromagnético surge si compactamos una dimensión extra en un radio muy pequeño. A primera vista, la posible existencia de nuevas dimensiones de muy pequeño tamaño puede parecer una idea demasiado especulativa; sin embargo, como vimos en otro artículo, el concepto de dimensión no es algo absoluto sino que depende de la energía a la que analicemos un sistema físico concreto. Una línea recta parece unidimensional a baja energía, pero si la analizamos de cerca a alta energía observaremos que en realidad tiene un grosor y por tanto es bidimensional como un cilindro: de hecho, la existencia en la naturaleza de objetos puntuales con diámetro cero es inconsistente. La teoría de KK implica la existencia de una quinta dimensión compactada en un círculo muy pequeño. Al examinar la dinámica de este espacio-tiempo de cinco dimensiones encontramos algo muy interesante: para un observador situado en las cuatro dimensiones macroscópicas, el movimiento de una partícula en la quinta dimensión es interpretado como la existencia de una carga eléctrica.

Esto implica algo fascinante: las dimensiones compactas tienen un efecto físico muy concreto en las dimensiones usuales. La fuerza electromagnética surge por el acoplamiento del campo gauge U(1) a una partícula cargada y esto último puede interpretarse como el momento de una partícula en una dimensión compacta. El modelo estándar se basa en la simetría gauge SU(3)xSU(2)XU(1). La primera simetría explica la fuerza nuclear fuerte, la segunda la fuerza nuclear débil y la tercera, como hemos visto, la fuerza electromagnética. La pregunta obvia es entonces : ¿Podemos describir el resto de fuerzas fundamentales añadiendo nuevas dimensiones compactas? Después de un enorme esfuerzo teórico para responder a esta pregunta, todos los intentos conducen hacia una misma teoría: la teoría de supercuerdas (TC). Como esta teoría está basada en 10 dimensiones y nuestro Universo macroscópico posee 4 dimensiones, deben existir 6 dimensiones compactadas. La forma de compactar estas 6 dimensiones extra produce diferentes contenidos de cargas y materia y dan lugar a las distintas clases de teorías de cuerdas.

Los microestados de los agujeros negros extremos

A continuación consideraremos un agujero negro con carga eléctrica total Q, concretamente un agujero negro extremo con carga Q=M. Los agujeros negros cargados están descritos por la métrica de Reissner-Nordström:

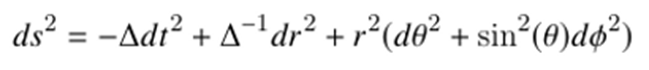
Donde:

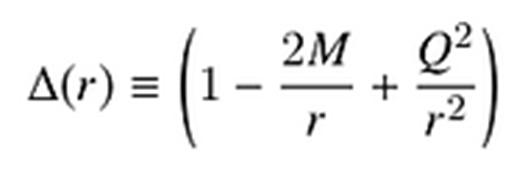
El horizonte de sucesos estará posicionado en el valor de r donde la métrica diverge. Para calcular su posición simplemente hacemos delta=0:

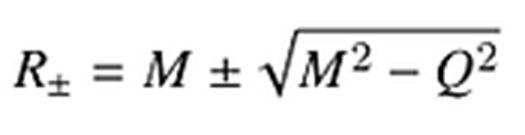
Este agujero negro tiene dos horizontes de sucesos: R+ y R- y podemos ver que para un determinado valor de la masa M, la posición de los horizontes solo depende de la carga Q. A nosotros nos interesa el caso concreto en el que el agujero negro tiene la máxima carga permitida: Q=M; este caso se denomina agujero negro extremo. En este caso, R+=R-=M, es decir, el agujero negro tiene solo un horizonte. Además, puede demostrarse fácilmente que en los agujeros negros extremos la radiación de Hawking es cero y por tanto las cargas Q son estables.

La fórmula de la entropía de Bekenstein-Hawking es una expresión universal que nos dice que la entropía de cualquier agujero negro con cualquier número de dimensiones es: S=A/4G. Donde A es el área del agujero negro (AN) y G es la constante de la gravitación de Newton. Esta entropía tiene que ser generada por un enorme número de microestados que deben de conformar la estructura cuántica fundamental de estos AN. La pregunta clave que nos hacemos en este artículo es: ¿Cuál es la naturaleza de ese enorme número de microestados? Siguiendo el trabajo iniciado por KK y desde el punto de vista de la utilización de nuevas dimensiones compactas ¿Podemos tratar de entender la estructura cuántica fundamental de los agujeros negros? Como veremos a continuación, la respuesta es afirmativa y el camino hacia la respuesta es fascinante.

Cargas, solitones y estados BPS en teoría de cuerdas

Antes de continuar necesitamos explicar brevemente tres "ingredientes" fundamentales de la teoría de cuerdas que necesitaremos para estudiar los microestados de los agujeros negros: los denominados estados BPS, los dos tipos de cargas y los denominados solitones de la teoría de cuerdas.

Los estados BPS

El acoplamiento g mide la "fuerza" con la que las cuerdas interactúan. El principal problema al que nos enfrentamos es que al aumentar este parámetro por encima de cierto valor, la métrica diverge y obtenemos un agujero negro. Sin embargo, en el caso concreto de AN extremos tenemos un cierto número de estados muy particulares denominados estados BPS. La principal ventaja de usar estos estados es que permanecen invariantes al variar g y por tanto su número es el mismo a bajo acoplamiento y a alto acoplamiento.

Las cargas de la teoría de cuerdas

La fuerza electromagnética surge cuando una partícula puntual cargada se acopla al campo de fuerza electromagnético. En la TC no existen las cargas puntuales, la carga está concentrada en los dos extremos de una cuerda. La fuerza electromagnética en TC surge cuando una cuerda cargada se acopla al equivalente al campo electromagnético en TC: el llamado campo de Kalb-Ramond. Este campo puede ser de dos tipos que dan lugar a los dos tipos de cargas en TC: las cargas NS (de Neveu-Schwarz) y las cargas RR (de Ramond). Estas cargas pueden ser tanto eléctricas como magnéticas. Aunque todo esto pueda parecer muy exótico, no es más que una generalización del campo electromagnético a un objeto extendido no puntual. Una cuerda cargada enrollada en una dimensión compactada es vista desde las dimensiones macroscópicas como una partícula puntual cargada.

Solitones de la teoría de cuerdas

Por último, además de los estados usuales correspondientes a las vibraciones de las cuerdas, existen otro tipo de estados denominados solitones. Estos estados son soluciones a las ecuaciones de movimiento de baja energía y constituyen configuraciones estables que portan una unidad fundamental de carga "magnética" de origen topológico.

El agujero negro extremo de cinco dimensiones en teoría de cuerdas

A continuación daremos el salto desde la relatividad general hasta la gravedad cuántica utilizando nuestra mejor herramienta disponible: la teoría de supercuerdas. En este artículo, nuestro objeto fundamental a estudiar será un agujero negro extremo de cinco dimensiones. Esta elección es solamente por simplicidad, debe de quedar claro que el estudio de un agujero negro de cuatro dimensiones también puede realizarse siguiendo un proceso equivalente.

Siguiendo la idea original de Kaluza y Klein, pero con unas herramientas teóricas mucho más avanzadas, vamos a ver qué sucede al compactar varias dimensiones. Puesto que la teoría de supercuerdas requiere diez dimensiones, usaremos entonces cinco dimensiones macroscópicas y cinco dimensiones microscópicas. El proceso que seguiremos será el siguiente:

1º) Compactaremos 4 dimensiones, por ejemplo la 6,7,8 y 9 en una "esfera 4D", más concretamente, en un toro-4D. De forma similar a como en la teoría de KK obtenemos un nuevo campo al compactar una dimensión extra, al compactar una 3-esfera obtenemos un nuevo campo que llamaremos H. La acción de la teoría de cuerdas en 6 dimensiones (obtenida al compactar cuatro) contiene el siguiente término:

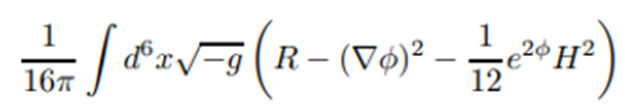
2º) Compactamos la dimensión 5 en un círculo de radio R mucho mayor que el de las otras 4 dimensiones compactadas. Entonces el término anterior se transforma en:

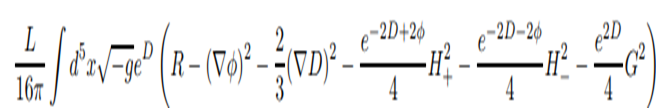
Ahora tenemos tres campos gauge con simetría U(1): H+, H- y G. H+ se obtiene al compactar la dimensión 5 en un círculo, H- se obtiene al compactar las dimensiones 6,7,8 y 9 y G es el usual campo de KK asociado al momento de una partícula (cuerda) en la dimensión 5. Siguiendo el más puro estilo de KK, ahora nos preguntamos: un observador situado en las cinco dimensiones macroscópicas ¿Qué cargas observará emanando de las dimensiones compactas? Nuestro observador macroscópico medirá tres cargas diferentes: una asociada al campo H+ en la dimensión circular 5, otra asociada al campo H- en las 4 dimensiones compactadas en un toro 4D y otra asociada al momento de una cuerda en la dimensión circular 5. Llamaremos a estas cargas Q1,Q5 y n respectivamente. El valor de las cargas Q1 y Q5 será proporcional a la superficie compactada de la que procede el campo de fuerza H. Por tanto tenemos:

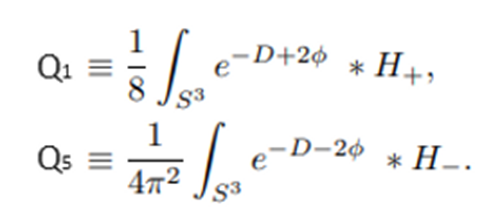
El valor de la última carga será proporcional al campo G que a su vez procede del movimiento en la dimensión 5:

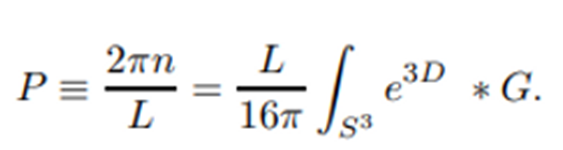
Ahora nos hacemos la siguiente pregunta: ¿Cuál es la entropía de este agujero negro? Para responder a esta pregunta primero debemos solucionar un "pequeño" problema: el horizonte del agujero negro es singular y por tanto no podemos evaluar su superficie para calcular la entropía. Sin embargo, el valor del parámetro alpha denominado "dilatón", puede ajustarse convenientemente. Existe un valor determinado de alpha para el cual las fuentes de Q1 y Q5 se cancelan mutuamente y por tanto se "estabilizan". Este valor es:

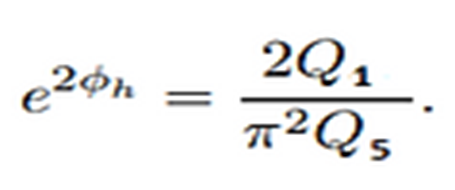
Ajustando el dilatón a este valor conseguimos estabilizar la métrica en el horizonte y obtenemos la siguiente métrica:

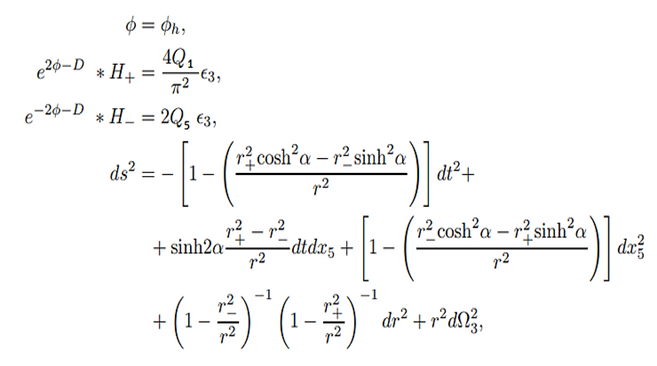
Esta expresión parece muy compleja e intimidante, pero visto desde las 5 dimensiones macroscópicas donde x5 es despreciable y tomando el caso de un AN extremo donde los dos horizontes coinciden, es decir: r+=r-=r_o obtenemos simplemente:

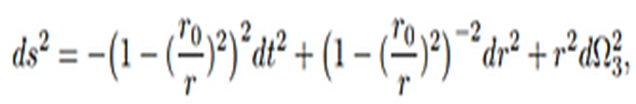
¡Esta es la métrica clásica obtenida por la relatividad general de un AN extremo de cinco dimensiones! ¡El AN extremo clásico de cinco dimensiones es una solución de las ecuaciones de baja energía de la teoría de supercuerdas!

El área del agujero negro es:

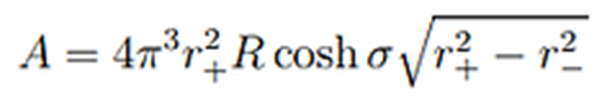
Y por tanto la entropía de nuestro agujero negro es:

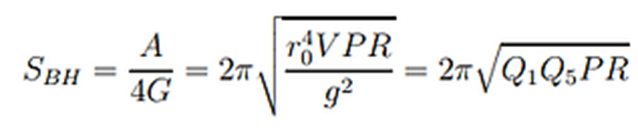
Como el momento P en la quinta dimensión compactada está cuantizado y vale P=n/R, tenemos finalmente:

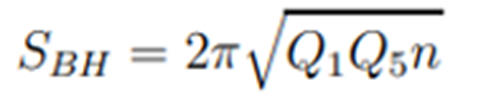
¿Podremos encontrar los microestados fundamentales que generan esta entropía?

Contando los estados fundamentales del agujero negro

Es ahora cuando afrontamos la pregunta clave: ¿Qué clase de objetos pueden generar esta entropía? ¿Podemos identificarlos utilizando la teoría de cuerdas?

Un agujero negro se produce cuando aumentamos el acoplamiento g por encima de cierto valor. Por encima de este valor la métrica diverge y no podemos hacer cálculos concretos. Sin embargo, debido a que los estados BPS no varían cuando aumentamos el acoplamiento, podemos contarlos a bajo acoplamiento y estar seguros de que al aumentar g el AN que obtenemos tiene el mismo número de estados BPS. La pregunta fundamental es: ¿Existe algún tipo de objeto que produzca estados BPS, que aporte una unidad de carga y que exista a bajo acoplamiento? En el caso de cargas RR la respuesta es afirmativa: este objeto se denomina D-Brana. De hecho una D-brana es un solitón similar a un monopolo magnético y por tanto porta a bajo acoplamiento exactamente una unidad de R carga. Por tanto el proceso que debemos seguir es el siguiente:

1º) Comenzamos a bajo acoplamiento con varios estados BPS que contienen R-cargas. El valor total de estas cargas será Qi. Estos estados pueden considerarse un estado ligado de varias D-branas.

2º) Aumentamos el acoplamiento g hasta obtener un agujero negro extremo de cinco dimensiones. Gracias a la invarianza respecto a g, los estados BPS no cambian y por tanto tendremos el mismo valor de la carga total Qi.

Llegados a este punto, la pregunta que nos queda por contestar es: a bajo acoplamiento ¿Cuántos estados BPS tenía nuestra carga inicial Qi? ¡Este número de estados inicial serán los que produzcan la entropía de nuestro AN final!

En el apartado anterior vimos que nuestro agujero negro porta 3 tipos de cargas: Q1,Q5 y n. ¿Qué tipo de objetos pueden generar estas cargas? ¿Cuántos estados BPS contienen a baja energía? Una 5-Dbrana enrollada una vez sobre las cinco dimensiones compactas porta una carga Q5=1. Una 1-Dbrana (una cuerda) enrollada una vez sobre la dimensión 5 porta una carga Q1=1. Las 1-Dbranas están pegadas a la 5-Dbrana pero son libres de moverse por las 4 dimensiones compactadas. Esto produce 4Q1 bosones sin masa: por tanto, esta configuración porta un número de estados BPS total de 4Q1Q5.

Por último, una cuerda con momento en la dimensión 5 porta un momento P=n/R. En teoría de campos, para n mucho mayor que R la entropía en una superficie bidimensional está dada por la fórmula:

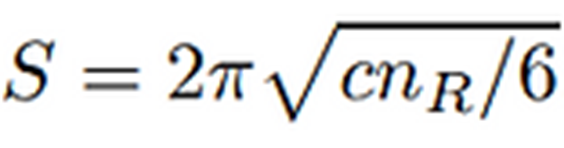
Donde c es una cantidad que en teoría de campos se denomina carga central. El valor de la carga central depende de la cantidad de fermiones-bosones. Para 4Q1Q5 bosones el valor de c es: 6Q1Q5. Por tanto la entropía final que obtenemos es:

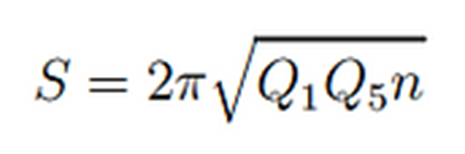
¡Esta es exactamente la entropía de Bekenstein-Hawking de nuestro agujero negro!

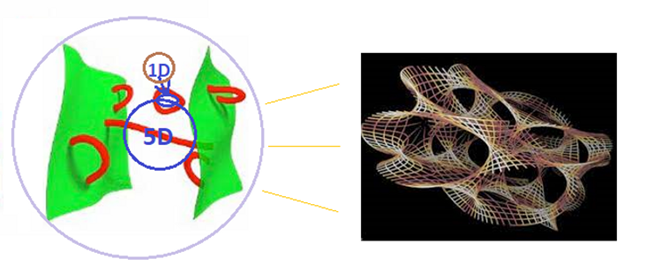
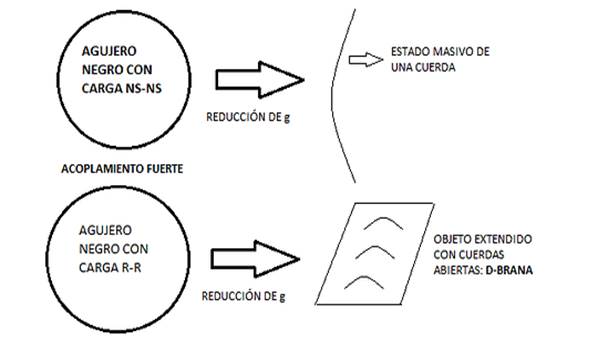
Izquierda: recreación de D-branas enrollando varias dimensiones compactadas y produciendo las cargas Q5 y Q1. La vibración de estos objetos extendidos produce los microestados del agujero negro en cinco dimensiones y determinan la posición del horizonte de sucesos. Derecha: si en lugar de compactar las dimensiones ocultas en un círculo o en un toro 4D las compactamos formando una geometría denominada variedad de Calabi-Yau podemos obtener los campos y las partículas del modelo estándar de la física de partículas.

Los componentes fundamentales del espacio-tiempo

En nuestro agujero negro de cinco dimensiones, la entropía es generada por la vibración de objetos extendidos penta dimensionales enrollados alrededor de las dimensiones 5,6,7,8 y 9 y de objetos uni dimensionales enrollados alrededor de la dimensión 5 (junto con cuerdas con momento desplazándose en la dimensión 5).

De forma similar puede calcularse que para un agujero negro más realista de cuatro dimensiones, la entropía es generada por 6D-branas enrolladas en las seis dimensiones compactas, 5D-branas enrolladas en 5 dimensiones compactas y 2D-branas enrolladas en dos de las dimensiones compactas (junto con cuerdas con momento desplazándose en una dimensión compacta).

Esto nos muestra algo realmente fascinante: la configuración de objetos extendidos sobre la geometría de las dimensiones compactas determina los microestados y el horizonte del agujero negro. Por tanto, un agujero negro, visto desde nuestras dimensiones macroscópicas, está formado por branas y cuerdas que vibran a través de las dimensiones ocultas.

¿Hemos encontrado por fin los componentes fundamentales del espacio-tiempo? Aunque parezca increíble, nuevos estudios teóricos parecen indicar que una de las dimensiones ocultas compactas de la teoría de cuerdas debe de estar en la escala del micrómetro y podría ser detectada en los próximos experimentos en curso.