LA LEY Y EL DESORDEN
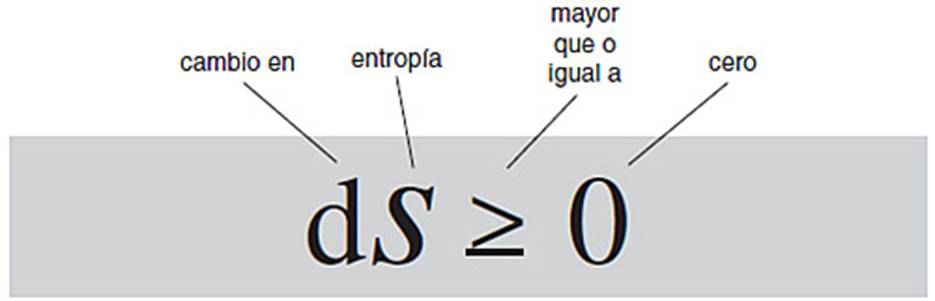
Segunda ley de la termodinámica
La cantidad de desorden en un sistema
termodinámico siempre aumenta. Pone límites a cuánto trabajo útil puede
extraerse a partir del calor. Provocó mejores máquinas de vapor, estimaciones de
la eficiencia de energía renovable, el escenario de «la gran congelación», la
prueba de que la materia está hecha de átomos, y conexiones paradójicas con la
flecha del tiempo.
En mayo de 1959, el físico y novelista
C.P. Snow dio una conferencia con el título The Two Cultures (Las dos
culturas), que provocó una extensa controversia. La respuesta del destacado
crítico literario F.R. Leavis fue la típica del otro bando de la discusión,
dijo rotundamente que había solo una cultura: la suya. Snow sugería que las
ciencias y las humanidades habían perdido contacto la una con la otra, y
argumentaba que esto estaba haciendo muy difícil solucionar los problemas del
mundo. Vemos lo mismo hoy en día con la negación del cambio climático y los
ataques a la evolución. La motivación puede ser diferente, pero las barreras
culturales ayudan a que prosperen estos sinsentidos, aunque es la política
quien lo maneja.
Snow estaba en particular descontento
con lo que veía como los estándares de la educación en declive, y afirmó:
“Un buen número de veces he estado
presente en reuniones de gente que, por los estándares de la cultura
tradicional, son consideradas eruditos y que han expresado con un entusiasmo
considerable su incredulidad sobre el analfabetismo de los científicos. Una o
dos veces se me ha provocado y he preguntado a quienes me acompañaban cuántos
de ellos podrían explicar la segunda ley de la termodinámica, la ley de la
entropía. La respuesta era fría, y también negativa. Aunque estaba preguntando
algo que es más o menos el equivalente científico de: «¿has leído algo de
Shakespeare?”.
Quizá sentía que estaba pidiendo
demasiado —muchos científicos cualificados no pueden enunciar la segunda ley de
la termodinámica—. Así que más tarde añadió:
“Ahora creo que incluso aunque hubiese
hecho una pregunta más simple, como qué quieres decir con masa, o aceleración,
que son el equivalente científico a «¿sabes leer?», no más de una décima parte
de los eruditos habrían sentido que yo estaba hablando el mismo idioma. De modo
que la gran estructura de la física moderna se construye, y la mayoría de la
gente más lista del mundo occidental tiene más o menos la misma capacidad para
comprenderlo que la que habrían tenido nuestros antepasados de la época
neolítica”.
Tomando a Snow al pie de la letra, mi
objetivo en este artículo es sacarnos
del Neolítico. La palabra «termodinámica» da una pista: parece querer decir la
dinámica del calor. ¿Puede el calor ser dinámico? Sí, el calor puede fluir.
Puede moverse de un lugar a otro, de un objeto a otro. Sal fuera en un día de
invierno y pronto sentirás frío. Fourier había escrito el primer modelo serio
del flujo del calor, e hizo algunas matemáticas bellas. Pero la principal razón
por la que los científicos se comenzaron a interesar por el flujo del calor fue
un objeto tecnológico modernísimo y muy rentable: la máquina de vapor.
Alrededor del 15 a.C., el arquitecto e
ingeniero romano Vitruvio describió una máquina llamada eolípila en su “De
Architectura”, y el matemático e ingeniero griego Herón de Alejandría construyó
una un siglo más tarde. Era una esfera hueca con algo de agua dentro, y dos
tubos sobresaliendo, curvados en un ángulo como en la siguiente figura.
Calienta la esfera y el agua se convierte en vapor, se escapa a través de los
extremos de los tubos y la reacción hace a la esfera girar. Fue la primera
máquina a vapor y demostró que el vapor podía hacer un trabajo, pero Herón no
hizo nada con ello, más allá de entretener a la gente. Hizo una máquina
parecida usando aire caliente en una cámara cerrada para tirar de una cuerda
que abría las puertas de un templo. Esta máquina tuvo una aplicación práctica,
produciendo un milagro religioso, pero no era una máquina de vapor.
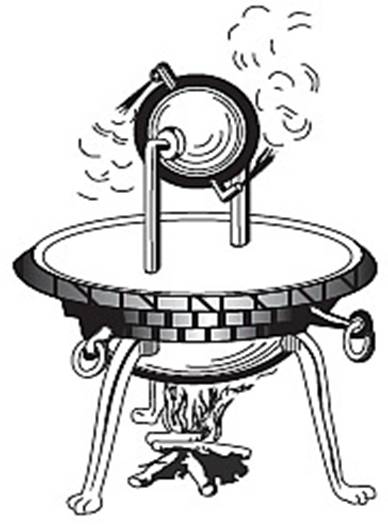
La eolípila de Herón
James Watt aprendió que el vapor podía
ser una fuente de fuerza en 1762 cuando tenía veintiséis años. No lo descubrió
observando una tetera; su amigo John Robinson, un profesor de filosofía natural
en la Universidad de Edimburgo, le habló sobre ello. Pero el poder del vapor
práctico era mucho más viejo. Su descubrimiento se atribuye con frecuencia al
ingeniero y arquitecto italiano Giovanni Branca, cuya Le Machine (La máquina)
de 1629 contenía 63 grabados de madera de aparatos mecánicos. Uno muestra una
rueda con pedales que giraría sobre su propio eje cuando el vapor de una
tubería chocase con sus paletas. Branca hizo conjeturas sobre lo útil que
podría ser esta máquina para moler harina, subir agua y cortar madera en
pedazos, aunque probablemente nunca se construyese. Era más un experimento
mental, un sueño mecánico imposible como la máquina voladora de Leonardo da
Vinci.
En cualquier caso, a Branca se le había
anticipado Taqi al-Din Muhammad ibn Ma’ruf al-Shami al-Asadi, quien vivió
alrededor de 1550 en el Imperio otomano y es reconocido ampliamente como el
mayor científico de su época. Sus logros son impresionantes. Trabajó en todo,
desde la astrología a la zoología, incluyendo relojería, medicina, filosofía y
teología, y escribió más de 90 libros. En su Al-turuq al-samiyya fi al-alat
al-ruhaniyya (Los métodos sublimes de las máquinas espirituales) de 1551,
al-Din describió una turbina de vapor primitiva, diciendo que podría usarse
para girar carne asada en un asador.
La primera máquina de vapor
verdaderamente práctica fue una bomba de agua inventada por Thomas Savery en
1698. La primera en obtener beneficios comerciales, construida por Thomas
Newcomen en 1712, disparó la Revolución Industrial. Pero la máquina de Newcomen
era muy poco eficiente. La contribución de Watt fue introducir un condensador
separado para el vapor, reduciendo la pérdida de calor. Desarrollada con dinero
proporcionado por el emprendedor Matthew Boulton, este nuevo tipo de máquina
solo usaba una cuarta parte de carbón, lo que suponía un ahorro enorme. La
máquina de Boulton y Watt comenzó a fabricarse en 1775, más de 220 años después
del libro de al-Din. En 1776, tres estaban listas y funcionando: una en una
mina de carbón en Tipton, una en una siderurgia en Shropshire y otra en
Londres.
Las máquinas de vapor realizaban varias
tareas industriales, pero con mucha diferencia la más común era bombear agua de
las minas. Costaba mucho dinero crear una mina, pero a medida que las capas
altas se quedaban sin trabajo y, los operadores estaban forzados a cavar más
profundo en la tierra y llegaban al nivel freático. Merecía la pena gastar
mucho dinero en bombear el agua fuera, ya que la alternativa era cerrar la mina
y empezar de nuevo en otro lugar, y eso podría no ser ni siquiera factible.
Pero nadie quería pagar más de lo que tenía que pagar, así que los fabricantes
que pudiesen diseñar y construir una máquina de vapor más eficiente
monopolizarían el mercado. De modo que la pregunta básica de cómo de eficiente
podría ser una máquina de vapor reclamaba a gritos atención. Su respuesta hizo
más que describir los límites de las máquinas de vapor; creó una rama nueva de
la física, cuyas aplicaciones casi no tenían límites. La nueva física arrojó
luz, sobre todo, desde los gases hasta la estructura de todo el universo; se
aplicó no solo a la materia inanimada de la física y la química, sino también a
los procesos complejos de la propia vida. Se llamó termodinámica: el movimiento
del calor. Y, al igual que la ley de la conservación de la energía en mecánica
descartó las máquinas mecánicas en perpetuo movimiento, las leyes de la
termodinámica descartaron máquinas similares usando calor.
Una de esas leyes, la primera ley de la
termodinámica, revela una nueva forma de energía asociada al calor, y extiende
la ley de conservación de la energía en el nuevo reino de los motores térmicos.
Otra, sin ningún precedente previo, muestra que algunas maneras potenciales de
intercambio de calor, las cuales no entran en conflicto con la conservación de
la energía, eran no obstante imposibles porque tendrían que crear orden a partir
del desorden. Esto era la segunda ley de la termodinámica.
Termodinámica es la física matemática
de los gases. Explica cómo características a gran escala, como la temperatura y
la presión, surgen a raíz del modo en que las moléculas de un gas interactúan.
El tema empieza con una serie de leyes de la naturaleza relacionadas con la
temperatura, la presión y el volumen. Esta versión se llama termodinámica
clásica y no hay moléculas involucradas, en esa época pocos científicos creían
en ellas. Más tarde, las leyes de los gases se consolidaron añadiendo otra capa
a la explicación, basada en un modelo matemático simple que involucraba
moléculas de modo explícito. Las moléculas de los gases eran imaginadas como
esferas minúsculas que rebotaban unas contra otras como bolas de billar
totalmente elásticas, sin perder energía en la colisión. Aunque las moléculas
no son esféricas, este modelo resultaba ser notablemente efectivo. Se llama la
teoría cinética de los gases, y condujo a la prueba experimental de que las moléculas
existían.
Estas primeras leyes de los gases
surgieron a rachas durante un período de cerca de cincuenta años, y se
atribuyen principalmente al físico y químico irlandés Robert Boyle, al
matemático y pionero en globos francés Jacques Alexandre César Charles, y al
físico y químico francés Joseph Louis Gay-Lussac. Sin embargo, muchos de los
descubrimientos fueron hechos por otros. En 1834, el ingeniero y físico francés
Émile Clapeyron combinó todas estas leyes en una, la ley de los gases ideales,
que ahora escribimos como:
pV = RT
Aquí p es la presión, V es el volumen,
T es la temperatura y R es una constante. La ecuación afirma que la presión por
el volumen es proporcional a la temperatura. Supuso mucho trabajo con muchos
gases diferentes para confirmar, experimentalmente, cada ley por separado, y la
síntesis global de Clapeyron. La palabra «ideal» aparece porque los gases
reales no obedecen la ley en todas las circunstancias, especialmente a
presiones altas donde las fuerzas interatómicas entran en juego. Pero la
versión ideal era lo suficientemente buena para diseñar máquinas de vapor. La
termodinámica está condensada en un número de leyes más generales, que no
dependen de la forma exacta de la ley del gas. Sin embargo, sí se necesita que
haya algo de dicha ley, porque la temperatura, la presión y el volumen no son
independientes. Tiene que haber alguna relación entre ellos, pero no importa
mucho cuál.
La primera ley de la termodinámica
surge de la ley mecánica de la conservación de la energía. Hay dos tipos
distintos de energía en mecánica clásica: la energía cinética, determinada por
la masa y la velocidad, y la energía potencial, determinada por el efecto de
fuerzas como la gravedad. Ninguno de estos tipos de energía se conserva por sí
solo. Si dejas caer un balón, la velocidad sube, de ese modo gana energía
cinética. También cae, perdiendo energía potencial. La segunda ley del
movimiento de Newton, implica que estos dos cambios se contrarrestan el uno con
el otro de manera exacta, de modo que la energía total no cambia durante el
movimiento.
No obstante, esta no es la historia
completa. Si pones un libro en una mesa y le das un empujón, su energía
potencial no cambia siempre que la mesa esté en horizontal. Pero su velocidad
sí que cambia, después de un incremento inicial producido por la fuerza con la
que lo empujas, el libro rápidamente se ralentiza y acaba en reposo. De modo
que la energía cinética empieza en un valor inicial distinto de cero justo
después del empujón, y luego desciende a cero. La energía total, por lo tanto,
también decrece, de manera que no se conserva la energía. ¿Dónde se ha ido?
¿Por qué el libro se para? Según la primera ley de Newton, el libro debería
continuar moviéndose, a menos que alguna fuerza se oponga. La fuerza es la fricción
entre el libro y la mesa. Pero ¿qué es la fricción?
La fricción ocurre cuando superficies
rugosas se frotan la una contra la otra. La superficie rugosa del libro tiene
pedacitos que sobresalen ligeramente. Estos entran en contacto con partes de la
mesa que también sobresalen ligeramente. El libro se roza con la mesa y la
mesa, obedeciendo la tercera ley de Newton, se resiste. Esto crea una fuerza
que se opone al movimiento del libro, de modo que disminuye su velocidad y
pierde energía. Así que, ¿adónde se va la energía? Quizá la conservación
simplemente no se aplica. Alternativamente, la energía está todavía merodeando
por algún lugar, pasando inadvertida. Y esto es lo que la primera ley de la
termodinámica nos dice: la energía desaparecida se presenta como calor. Tanto
el libro como la mesa se calientan ligeramente.
Los humanos hemos sabido que la fricción
crea calor ya desde que alguien descubrió cómo frotar dos palos el uno contra
el otro para empezar un fuego. Si deslizas tus manos por una cuerda demasiado
rápido, te las quemarás a causa de la fricción con la cuerda. Había un montón
de indicios.
La primera ley de la termodinámica
afirma que el calor es una forma de energía, y la energía, con esta ampliación,
se conserva en los procesos termodinámicos. La primera ley de la termodinámica
pone límites a lo que puedes hacer con un motor térmico. La cantidad de energía
cinética que puedes sacar, en la forma de movimiento, no puede ser más que la
cantidad de energía que introduces como calor. Pero resultó que había una
restricción adicional en cómo un motor térmico puede convertir energía térmica
en energía cinética de modo eficiente; no solo el apunte práctico de que algo
de energía siempre se pierde, sino un límite teórico que impide que toda la energía
térmica sea convertida en movimiento. Solo alguna de ella, la energía «libre»,
puede ser convertida. La segunda ley de la termodinámica convierte esta idea en
un principio general, pero nos hará falta un rato para llegar a ello. La
limitación fue descubierta por Nicolas Léonard Sadi Carnot en 1824, en un
modelo simple de cómo funciona una máquina de vapor: el ciclo de Carnot.
Para entender el ciclo de Carnot es
importante distinguir entre calor y temperatura. En la vida cotidiana, decimos que
algo está caliente si su temperatura es alta, y así confundimos los dos
conceptos. En la termodinámica clásica, ningún concepto es tan sencillo. La
temperatura es una propiedad de un fluido, pero el calor solo tiene sentido
como una medida de la transferencia de energía entre fluidos, y no es una
propiedad intrínseca del estado del fluido (esto es, la temperatura, presión y
volumen).
En la teoría cinética, la temperatura
de un fluido es la energía cinética media de sus moléculas, y la cantidad de
calor transferido entre fluidos es el cambio en la energía cinética total de
sus moléculas. En cierto sentido, el calor es un poco como la energía
potencial, que se define en relación con una altura de referencia arbitraria;
esto introduce una constante arbitraria, de modo que «la» energía potencial de
un cuerpo no está definida de manera única. Pero cuando el cuerpo cambia de
altura, la diferencia en las energías potenciales es la misma sea cual sea la
altura de referencia usada, porque la constante la contrarresta. En resumen, la
medición del calor cambia, pero la medición de la temperatura se estipula. Las
dos están vinculadas; la transferencia de calor es posible solo cuando los
fluidos afectados tienen temperaturas diferentes, y entonces se transfiere del
más caliente al más frío. Esto es llamado con frecuencia el principio cero de
la termodinámica porque lógicamente precede a la primera ley, pero
históricamente fue reconocido más tarde.
La temperatura puede medirse usando un
termómetro, que se aprovecha de la expansión de un fluido, como el mercurio,
causada por el incremento de la temperatura. El calor puede medirse usando su
relación con la temperatura. En un fluido de prueba estándar, como el agua,
cada grado que aumenta la temperatura de un gramo de fluido se corresponde con
un incremento fijo en el contenido de calor. Esta cantidad es llamada el calor
específico del fluido, que en el agua es una caloría por gramo por grado
Celsius. Observa que el incremento de calor es un cambio, no un estado, como
exige la definición de calor. Podemos visualizar el ciclo de Carnot pensando en
una cámara que contiene gas, con un émbolo móvil en un extremo. El ciclo consta
de cuatro pasos:
1. Calienta el gas tan rápidamente que
su temperatura no cambie. Se expande, realizando trabajo sobre el émbolo.
2. Permite al gas expandirse más,
reduciendo la presión. El gas se enfría.
3. Comprime el gas tan rápidamente que
su temperatura no cambie. El émbolo ahora realiza trabajo sobre el gas.
4. Permite al gas expandirse más,
incrementando la presión. El gas vuelve a su temperatura original.
En un ciclo de Carnot, el calor
introducido en el primer paso transfiere energía cinética al émbolo,
permitiendo a este hacer el trabajo. La cantidad de energía transferida puede
calcularse en términos de la cantidad de calor introducido y la diferencia de
temperatura entre el gas y lo que lo rodea. El teorema de Carnot prueba que, en
principio, un ciclo de Carnot es el modo más eficiente de convertir calor en
trabajo. Esto pone un límite riguroso sobre la eficiencia de cualquier motor
térmico y, en particular, sobre una máquina de vapor.
En un diagrama que muestra la presión y
el volumen del gas, un ciclo de Carnot tiene el aspecto de la siguiente figura
(izquierda). El físico y matemático alemán Rudolf Clausius descubrió una manera
más simple de visualizar el ciclo, figura (derecha). Ahora los ejes son la
temperatura y una cantidad nueva y fundamental llamada entropía. Con estas
coordenadas, el ciclo se hace un rectángulo y la cantidad de trabajo realizado
es justo el área del rectángulo.
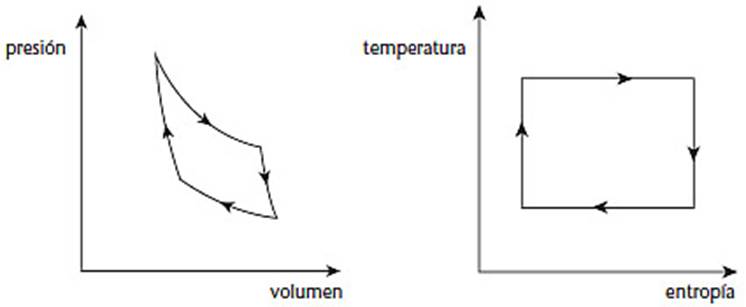
El ciclo de Carnot. A la
izquierda en términos de presión y volumen. A la derecha en términos de
temperatura y entropía
La entropía es como el calor: está
definida en términos de un cambio de estado, no un estado como tal. Supón que
un fluido en algún estado inicial cambia a un nuevo estado. Entonces la
diferencia de entropía entre los dos estados es el cambio total en la cantidad
«calor dividido entre temperatura». En símbolos, para un pequeño paso a lo
largo de un camino entre los dos estados, la entropía S está relacionada con el
calor Q y la temperatura T por la ecuación diferencial
dS = dQ/T
El cambio en la entropía es el cambio
en el calor por unidad de temperatura. Un cambio grande de estado puede
representarse como una serie de pequeños, de modo que sumamos todos estos
cambios pequeños en la entropía para obtener el cambio total de entropía. El
cálculo nos dice que el modo de hacer esto es usar una integral. Una vez
definida la entropía, la segunda ley de la termodinámica es muy simple. Afirma
que en cualquier proceso termodinámico físicamente factible, la entropía de un
sistema aislado debe siempre aumentar. En símbolos,
dS ≥ 0.
Por ejemplo, supón que dividimos una
habitación con una mampara móvil, ponemos oxígeno en un lado de la mampara y
nitrógeno en el otro. Cada gas tiene una entropía concreta, relacionada con
algún estado de referencia inicial. Ahora elimina la mampara, permitiendo a los
dos mezclarse. El sistema combinado también tiene una entropía concreta,
relacionada con los mismos estados de referencia iniciales. Y la entropía del
sistema combinado es siempre mayor que la suma de las entropías de los dos
gases por separado.
La termodinámica clásica es
fenomenológica: describe lo que puedes medir, pero no está basada en ninguna
teoría coherente del proceso implicado. Ese fue el siguiente paso en la teoría
cinética de los gases, promovido por Daniel Bernoulli en 1738. Esta teoría
proporciona una explicación física de la presión, la temperatura, las leyes de
los gases y esa cantidad misteriosa de la entropía. La idea básica, muy
polémica en su época, es que un gas consiste en un gran número de moléculas
idénticas, que van dando tumbos por el espacio y ocasionalmente chocan unas con
otras. Ser un gas significa que las moléculas no están muy apretujadas, de modo
que cualquier molécula dada pasa mucho de su tiempo viajando a través del vacío
a una velocidad constante en línea recta. (Digo «vacío» incluso aunque estemos
hablando de un gas, porque esto es en lo que consiste el espacio entre
moléculas.) Como las moléculas, aunque sean muy pequeñas, tienen un tamaño
distinto de cero, de vez en cuando dos de ellas colisionan. La teoría cinética
hace la suposición simplificadora de que rebotan como dos bolas de billar que
chocan, y que estas bolas son totalmente elásticas, de manera que no se pierde
ninguna energía en la colisión. Entre otras cosas, esto implica que las
moléculas se mantienen rebotando para siempre.
Cuando Bernoulli propuso el modelo por
primera vez, la ley de la conservación de la energía no estaba establecida y la
elasticidad parecía poco probable. La teoría gradualmente ganó apoyo de un
pequeño número de científicos, que desarrollaron sus propias versiones y
añadieron varias ideas nuevas, pero su trabajo fue ignorado casi
universalmente. El químico y físico alemán August Krönig escribió un libro
sobre el tema en 1856, simplificando la física al no permitir a las moléculas
rotar. Clausius eliminó esta simplificación un año más tarde. Afirmó que había
llegado a sus resultados independientemente, y ahora está considerado como uno
de los primeros fundadores significativos de la teoría cinética. Propuso uno de
los conceptos clave de la teoría, el camino libre medio de una molécula: con
qué rapidez se desplaza, de media, entre colisiones sucesivas.
Tanto König como Clausius dedujeron la
ley de los gases ideales de la teoría cinética. Las tres variables clave son
volumen, presión y temperatura. El volumen está determinado por el envase que
contiene al gas, establece las «condiciones de frontera» que afecta a cómo el
gas se comporta, pero no es una característica del gas como tal. La presión es
la fuerza media (por unidad cuadrada de área) ejercida por las moléculas del
gas cuando colisionan con las paredes del envase. Esto depende de cuántas
moléculas están dentro del envase y cómo de rápido se mueven. (No se mueven
todas a la misma velocidad.) Más interesante es la temperatura. Esta también
depende de la rapidez con que se estén moviendo las moléculas del gas, y es
proporcional a la energía cinética media de las moléculas. Deducir la ley de
Boyle, el caso especial de la ley de los gases ideales para una temperatura
constante, es especialmente sencillo. Con una temperatura fija, la distribución
de las velocidades no cambia, de modo que la presión está determinada por
cuántas moléculas golpean la pared. Si reduces el volumen, el número de
moléculas por unidad cúbica de espacio sube, y la posibilidad de que cualquier
molécula golpee la pared aumenta también. Un volumen más pequeño quiere decir
un gas más denso, que quiere decir más moléculas golpeando la pared, y este
argumento puede hacerse cuantitativo.
Argumentos similares pero más
complicados dan lugar a la ley de los gases ideales en toda su gloria, siempre
y cuando las moléculas no se aplasten unas contra otras con demasiada fuerza.
De modo que ahora había unas bases teóricas más profundas para la ley de Boyle,
basada en la teoría de moléculas. A Maxwell le inspiró el trabajo de Clausius,
y en 1859 puso la teoría cinética sobre fundamentos matemáticos escribiendo una
fórmula para la probabilidad de que una molécula se desplazase a una velocidad
dada. Se basa en la distribución normal o campana de Gauss. La fórmula de
Maxwell parece haber sido el primer ejemplo de una ley física basada en la
probabilidad. Le siguió el físico austríaco Ludwig Boltzmann, quien desarrolló
la misma fórmula, ahora llamada la distribución de Maxwell-Boltzmann. Boltzmann
reinterpretó la termodinámica en términos de la teoría cinética de gases,
fundando lo que ahora se llama mecánica estadística. En particular, dio con una
interpretación nueva de entropía, relacionando el concepto de termodinámica con
una característica estadística de las moléculas en el gas.
Todas las cantidades termodinámicas
tradicionales, como la temperatura, presión, calor y entropía, se refieren a
propiedades medias a gran escala del gas. Sin embargo, la estructura menuda
consiste en muchas moléculas que pasan zumbando por todas partes y chocan unas
contra otras. El mismo estado a gran escala puede surgir de innumerables
estados diferentes a pequeña escala, debido a que las diferencias menores en la
escala pequeña se compensan con la media. Boltzmann, por lo tanto, distinguía
macroestados de microestados del sistema: promedios a gran escala y el estado
real de las moléculas. Usando esto, mostró que la entropía, un macroestado,
puede interpretarse como una característica estadística de microestados. Lo
expresó en la ecuación:
S = k log W
Donde S es la entropía del sistema, W
es el número de microestados distintos que pueden dar lugar al macroestado
total, y k es una constante. Ahora se llama constante de Boltzmann, y su valor
es 1,38 × 10–23 julios por grado Kelvin. Es esta fórmula la que
motiva la interpretación de la entropía como desorden. La idea es que menos
microestados se corresponden con un macroestado más ordenado que con uno
desordenado, y podemos comprender por qué si pensamos en barajas de cartas.
Para simplificar, supón que tenemos solo seis cartas marcadas con 2, 3, 4, J,
Q, K. Ponlas en dos montones separados, con las cartas de valor bajo en un
montón y las figuras en el otro. Esto es una disposición ordenada. De hecho,
mantiene restos de un orden si barajas cada montón, pero mantienes los montones
por separado, porque aunque barajes, las cartas de valor bajo están en un
montón y las figuras están en el otro. Sin embargo, si barajas los dos montones
juntos, los dos tipos de cartas pueden mezclarse, con disposiciones como
4QK2J3. Intuitivamente, estas disposiciones revueltas son más desordenadas.
Veamos cómo se relaciona esto con la
fórmula de Boltzmann. Hay 36 modos de colocar las cartas en dos montones, seis
para cada montón. Pero hay 720 modos (6! = 1 × 2 × 3 × 4 × 5 × 6) de colocar
las 6 cartas. El tipo de orden de las cartas que permitimos (dos montones o
uno) es análogo al macroestado de un sistema termodinámico. El orden exacto es
el microestado. El macroestado más ordenado tiene 36 microestados, el menos
ordenado tiene 720. Así que cuantos más microestados haya, menos ordenado pasa
a estar el macroestado correspondiente. Ya que cuanto mayor es un número, mayor
es su logaritmo, cuanto mayor es el logaritmo del número de microestados, más
desordenado está el macroestado. En este caso: log 36 = 3,58 log 720 = 6,58. Estas son realmente las
entropías de los dos macroestados. La constante de Boltzmann solo escala los
valores para adecuarlos al formalismo de la termodinámica cuando estamos
tratando con gases.
Los dos montones de cartas son como dos
estados termodinámicos que no interactúan, como una caja con un tabique
separando dos gases. Las entropías individuales de cada uno son log 6, así que
la entropía total es 2 ·log 6, que es igual a log 36. De modo que el logaritmo
hace a la entropía aditiva para sistemas que no interactúan; para obtener la
entropía de un sistema combinado (pero que no está interactuando), suma las
entropías sueltas. Si ahora permitimos a los sistemas interactuar (eliminamos
el tabique) la entropía incrementa a log 720. Cuantas más cartas hay, más
pronunciado se hace este efecto. Divide una baraja francesa estándar de 52 cartas
en dos montones, con todas las cartas rojas en un montón y todas las negras en
otro. Esta disposición puede darse de (26!)2 modos, lo que es alrededor de 1,63
× 1053. Barajando los dos montones, obtenemos 52! microestados,
aproximadamente 8,07 × 1067. Los logaritmos son 122,53 y 156,36
respectivamente y, de nuevo, el segundo es mayor.
Las ideas de Boltzmann no fueron
recibidas con grandes vítores. A un nivel técnico, la termodinámica estaba
plagada de asuntos conceptuales difíciles. Uno era el significado exacto de
«microestado». La posición y la velocidad de una molécula son variables
continuas, capaces de tomar infinidad de valores, pero Boltzmann necesitaba un número
finito de microestados para poder contar cuántos había y luego calcular el
logaritmo. Así que estas variables tenían que ser «toscas» en cierto modo,
dividiendo el continuo de los posibles valores en un número finito de
intervalos muy pequeños. Otro asunto, de naturaleza más filosófica, era la
flecha del tiempo, un conflicto aparente entre la dinámica reversible del
tiempo de los microestados y el tiempo unidireccional de los macroestados,
determinado por el incremento de la entropía. Los dos asuntos están
relacionados, como veremos en breve.
Sin embargo, el mayor obstáculo para la
aceptación de la teoría era la idea de que la materia está hecha de partículas
extremadamente pequeñas, los átomos. Este concepto, y la palabra átomo, que
significa «indivisible», se remonta a la Grecia Clásica, aunque todavía
alrededor de 1900 la mayoría de los físicos no creían que la materia estuviese
hecha de átomos. De modo que tampoco creían en las moléculas y una teoría de
gases basada en ellas era obviamente un sinsentido. Maxwell, Boltzmann y otros
pioneros de la teoría cinética estaban convencidos de que las moléculas y los
átomos eran reales, pero para los escépticos, la teoría atómica era solo un
modo conveniente de imaginarse la materia. No se habían observado átomos nunca,
de modo que no había evidencias científicas de que existiesen. Las moléculas,
combinaciones específicas de átomos, eran igualmente polémicas. Sí, la teoría
atómica encajaba con todo tipo de datos experimentales en química, pero no
había prueba de que los átomos existiesen.
Una de las cosas que finalmente
convenció a la mayoría de objetores fue el uso de la teoría cinética para hacer
predicciones sobre el movimiento browniano. Este efecto fue descubierto por un botánico
escocés, Robert Brown. Fue pionero en el uso del microscopio, descubriendo,
entre otras cosas, la existencia de los núcleos de una célula, ahora conocidos
por ser el almacén de su información genética. En 1827, Brown estaba viendo a
través de su microscopio los granos de polen en un fluido y descubrió
partículas incluso más pequeñas que habían sido expulsadas por el polen. Estas
partículas diminutas se mueven de un lado a otro de una manera aleatoria, y al
principio Brown se preguntó si eran alguna forma diminuta de vida. Sin embargo,
sus experimentos mostraron el mismo efecto en las partículas obtenidas de
materia no viva, de modo que fuese lo que fuese lo que causaba el movimiento,
no tenía que estar vivo. En la época, nadie sabía qué causaba este efecto.
Ahora sabemos que las partículas expulsadas por el polen son orgánulos,
subsistemas minúsculos de células con funciones específicas, en este caso, para
fabricar almidón y grasas. E interpretamos su movimiento aleatorio como la
prueba para la teoría de que la materia está hecha de átomos.
El vínculo con los átomos viene de
modelos matemáticos del movimiento browniano, que primero aparecieron en un
trabajo estadístico del astrónomo y actuario danés Thorvald Thiele en 1880. El
gran avance fue hecho por Einstein en 1905 y el científico polaco Marian
Smoluchowski en 1906. De manera independiente propusieron una explicación
física para el movimiento browniano: los átomos del fluido en el que las
partículas están flotando están aleatoriamente chocando con las partículas y
dándoles patadas diminutas. Partiendo de esto, Einstein usó un modelo
matemático para hacer predicciones cuantitativas sobre la estadística del
movimiento, que fueron confirmadas por Jean Baptiste Perrin en 1908-1909.

Boltzmann se suicidó en 1906, justo
cuando el mundo científico estaba empezando a apreciar que las bases de su
teoría eran reales. En la formulación de Boltzmann de termodinámica, las
moléculas en un gas son análogas a las cartas en una baraja, y la dinámica
natural de las moléculas es análoga a barajar. Supongamos que en algún momento
todas las moléculas de oxígeno en una habitación se concentran en un extremo, y
todas las de nitrógeno en el otro. Esto es un estado termodinámico ordenado,
como los dos montones de cartas separados. Sin embargo, después de un período
muy corto, colisiones aleatorias mezclarán todas las moléculas, más o menos
uniformemente, por toda la habitación, como barajar las cartas. Acabamos de ver
que este proceso habitualmente provoca que la entropía se incremente. Esta es
la imagen ortodoxa del incremento implacable de la entropía, y es la
interpretación estándar de la segunda ley:
«la cantidad de desorden
en el universo incrementa a ritmo constante».
Esta caracterización de la segunda ley habría
satisfecho a Snow si alguien la hubiese ofrecido. En esta forma, una
consecuencia dramática de la segunda ley es el escenario de la «Gran
congelación», en el cual todo el universo se acabará convirtiendo en un gas
tibio con una estructura para nada interesante. La entropía, y el formalismo
matemático que la acompaña, proporcionan un modelo excelente para muchas cosas.
Explica por qué los motores térmicos pueden alcanzar solo un nivel de
eficiencia concreto, que evita que los ingenieros gasten un tiempo y dinero
valiosos buscando resultados que no van a ningún lado. Esto no solo es cierto
para las máquinas a vapor de la época victoriana, también se aplica para los
motores de los coches modernos. El diseño de motores es una de las áreas
prácticas que se ha visto beneficiada por el conocimiento de las leyes de la
termodinámica. Los frigoríficos son otra. Usan reacciones químicas para
transferir calor fuera de la comida en la nevera. Tiene que ir a algún lado,
con frecuencia puedes sentir el calor saliendo del exterior del compartimento
del motor del frigorífico. Lo mismo ocurre con el aire acondicionado. La
generación de energía es otra aplicación. En una central de energía de carbón,
de gas o nuclear, lo que es generado inicialmente es calor. El calor crea
vapor, que activa una turbina. La turbina, siguiendo principios que se remontan
a Faraday, convierte el movimiento en electricidad.
La segunda ley de la termodinámica
también determina la cantidad de energía que podemos esperar extraer de
recursos renovables como el viento o las olas. El cambio climático ha añadido
una nueva urgencia a esta cuestión, porque las fuentes de energía renovable
producen menos dióxido de carbono que las convencionales. Incluso las centrales
nucleares tienen un gran impacto de carbono, porque el combustible tiene que
hacerse, transportarse y almacenarse cuando ya no es útil pero todavía es
radiactivo. Hay debate sobre la cantidad máxima de energía que podemos extraer
del océano y la atmósfera sin causar el tipo de cambio que estamos intentando
evitar. Está basado en las estimaciones termodinámicas de la cantidad de
energía libre en esos sistemas naturales.
Esto es un asunto importante; si las
renovables en principio no pueden aportar la energía que necesitamos, tenemos
que buscar en otro lado. Los paneles solares, que extraen energía directamente
de la luz del sol, no se ven afectados directamente por los límites de la
termodinámica, pero incluso estos implican procesos de fabricación. En este
momento, ver dichos límites como un obstáculo serio recae en algunas
simplificaciones radicales, e incluso aunque sean correctas, los cálculos no
descartan las renovables como una fuente para la mayoría de la energía del
mundo. Pero merece la pena recordar que de manera similar cálculos amplios
sobre la producción de dióxido de carbono, realizados en la década de 1950, han
probado ser sorprendentemente precisos en la predicción del calentamiento
global.
La segunda ley funciona de manera
brillante en su contexto original, el comportamiento de los gases, pero parece
entrar en conflicto con las ricas complejidades de nuestro planeta, en
concreto, la vida. Parece excluir la complejidad y organización exhibida por
los sistemas vivos. De modo que la segunda ley es a veces invocada para atacar
la evolución darwiniana. Sin embargo, la física de las máquinas de vapor no es
particularmente apropiada para el estudio de la vida. En la teoría cinética de
gases, las fuerzas que actúan entre las moléculas son de corto alcance (activas
solo cuando las moléculas colisionan) y repulsivas (rebotan). Pero la mayoría
de las fuerzas de la naturaleza no son así. Por ejemplo, la gravedad actúa en
distancias enormes y es atractiva. La expansión del universo a partir del Big
Bang no ha emborronado la materia convirtiéndola en un gas uniforme. En su
lugar, la materia se ha agrupado: planetas, estrellas, galaxias,
supercúmulos... Las fuerzas que mantienen las moléculas unidas son también
atractivas, excepto en distancias muy cortas, donde se hacen repulsivas, lo que
evita que las moléculas colapsen, pero su alcance efectivo es bastante corto.
Para sistemas como estos, el modelo
termodinámico de subsistemas independientes cuyas interacciones se encienden
pero no se apagan es simplemente irrelevante. Las características de la termodinámica
tampoco se aplican, o se hace tan a largo plazo que no son el modelo de nada
interesante. Entonces, las leyes de la termodinámica sustentan muchas cosas que
damos por hecho. Y la interpretación de la entropía como «desorden» nos ayuda a
entender esas leyes y ganar un sentimiento intuitivo para sus bases físicas.
Sin embargo, hay ocasiones en las que interpretar la entropía como desorden
parece llevar a paradojas. Esto es una esfera más filosófica del discurso, y es
fascinante.
Uno de los misterios más profundos de
la física es la flecha del tiempo. El tiempo parece fluir en una dirección
concreta. Sin embargo, parece posible lógica y matemáticamente para el tiempo
fluir hacia atrás, una posibilidad explotada por libros como “La flecha del
tiempo” de Martin Amis, la novela mucho más temprana “El mundo contra reloj “de
Philip K. Dick, y la serie de televisión de la BBC “Enano rojo”, cuyos
protagonistas memorablemente bebieron cerveza y participan en una pelea de bar
en el tiempo marcha atrás. De modo que, ¿por qué no puede fluir el tiempo en el
otro sentido? A primera vista, la termodinámica ofrece una explicación simple
para la flecha del tiempo: es la dirección del incremento de la entropía. Los
procesos termodinámicos son irreversibles: el oxígeno y el nitrógeno se
mezclarán espontáneamente, pero no se desmezclarán espontáneamente.
Sin embargo, aquí hay un enigma, porque
cualquier sistema mecánico clásico, como las moléculas en una habitación, es
reversible en el tiempo. Si continúas barajando un montón de cartas de modo
aleatorio, entonces finalmente volverán a su orden original. En las ecuaciones
matemáticas, si en algún instante las velocidades de todas las partículas se
invierten simultáneamente, entonces el sistema remontará sus pasos al revés en
el tiempo. El universo entero puede rebotar, obedeciendo las mismas ecuaciones
en ambas direcciones. De modo que, ¿por qué nunca vemos un huevo
desrevueltándose? La respuesta termodinámica habitual es: un huevo revuelto
está más desordenado que uno no revuelto, la entropía aumenta, y ese es el modo
de fluir del tiempo. Pero hay una razón sutil por la que los huevos no se
desrevueltan: es muy, muy, muy poco probable que el universo rebote de la
manera necesaria. La probabilidad de que suceda es ridículamente pequeña.
De modo que la discrepancia entre el
incremento de la entropía y la reversibilidad del tiempo viene de las
condiciones iniciales, no de las ecuaciones. Las ecuaciones para moléculas en
movimiento son reversibles en el tiempo, pero las condiciones iniciales no.
Cuando invertimos el tiempo debemos usar condiciones «iniciales» dadas por el
estado final del movimiento del tiempo hacia delante. La distinción más
importante aquí es entre la simetría de las ecuaciones y la simetría de sus
soluciones. Las ecuaciones para moléculas que rebotan tienen simetría
reversible en el tiempo, pero las soluciones individuales pueden tener una
flecha del tiempo definitiva. Cuanto más puedes deducir sobre una solución, a
partir de la reversibilidad del tiempo de la ecuación, es que debe existir
también otra solución que es reversible en el tiempo de la primera. Si Alicia
lanza una pelota a Roberto, la solución reversible en el tiempo es Roberto
lanzándole una pelota a Alicia. De modo similar, como las ecuaciones de la
mecánica permiten a un vaso caer al suelo y romperse en mil pedazos, deben
también permitir una solución en la cual miles de fragmentos de cristal
misteriosamente se muevan juntos y se unan entre sí formando un vaso intacto y
que salte en el aire.
Claramente hay algo extraño en eso, y
requiere investigarlo. No tenemos problema con Roberto y Alicia lanzándose un
balón en cualquier sentido. Vemos cosas así cada día. Pero no vemos un vaso
romperse y luego recomponerse por sí solo. No vemos un huevo desrevueltándose.
Supón que rompemos un vaso y grabamos el resultado. Empezamos con un estado
ordenado y simple: un vaso intacto. Cae al suelo, donde el impacto hace que se
rompa en pedazos y lanza esos pedazos por todo el suelo. Estos se van frenando
hasta que se detienen. Todo parece completamente normal. Ahora rebobina la
película. Trozos de cristal, que resultan tener justo la forma correcta para
encajar unos con otros, están esparcidos por el suelo. Espontáneamente empiezan
a moverse. Se mueven justo a la velocidad correcta, y justo en la dirección
correcta, para encontrarse. Se ensamblan formando un vaso, que se dirige hacia
el cielo.
No parece que esté bien. De hecho, como
está descrito, no es correcto. Varias leyes de la mecánica parecen violarse,
entre ellas la conservación del momento y la conservación de la energía. Masas
que no están en movimiento no pueden de repente moverse. Un vaso no puede ganar
energía de ninguna parte para saltar en el aire. Ah, sí... pero eso es porque
no estamos observando con la suficiente atención. El vaso no salta en el aire
motu propio. El suelo empieza a vibrar, y las vibraciones se juntan para dar al
vaso una repentina patada al aire. Los trozos de cristal de manera similar
fueron impulsados a moverse por ondas entrantes de vibración del suelo. Si
trazamos esas vibraciones hacia atrás, se extienden, y parecen extinguirse.
Finalmente la fricción disipa todo movimiento... Oh, sí, fricción. ¿Qué sucede
con la energía cinética cuando hay fricción? Se convierte en calor. Así que hemos
omitido algunos detalles del escenario del tiempo reversible. El momento y la
energía se mantienen en equilibrio, pero las cantidades omitidas provienen del
suelo perdiendo calor.
En principio, podemos establecer un
sistema hacia delante en el tiempo para imitar el vaso en el tiempo invertido.
Tan solo tenemos que inducir a las moléculas en el suelo a colisionar justo del
modo correcto para liberar algo de su calor como movimiento del suelo, dar una
patada a los trozos de cristal justo en el modo correcto, luego arrojar el vaso
al aire. El asunto no es que sea imposible en principio, si lo fuera, la
reversibilidad del tiempo fracasaría. Sino que es imposible en la práctica, ya
que no hay modo de controlar tantas moléculas de un modo tan exacto. Esto también
es un tema sobre las condiciones frontera, en este caso las condiciones
iniciales. Las condiciones iniciales para el experimento del vaso rompiéndose
son fáciles de implementar, y el equipo es fácil de adquirir. Todo es muy
robusto también; usa otro vaso, lánzalo desde una altura diferente... sucederá
prácticamente lo mismo. El experimento del vaso ensamblándose, por el
contrario, necesita un control extraordinariamente preciso de infinidad de
moléculas individuales y trozos de cristal hechos con sumo cuidado. Y sin que
todo ese equipo de control moleste a una sola molécula. Es por esto por lo que
no podemos hacerlo en realidad.
No obstante, observa cómo estamos
pensando aquí; nos estamos centrando en condiciones iniciales. Eso establece
una flecha del tiempo, el resto de la acción viene después del comienzo. Si
viésemos las condiciones finales del vaso rompiéndose, bajando al nivel
molecular, serían tan complejas que nadie en su sano juicio consideraría
intentar replicarlas.
Las matemáticas de la entropía esquivan
estas consideraciones a escala muy pequeña. Permite a las vibraciones
extinguirse pero no aumentar. Permite a la fricción convertirse en calor, pero
no al calor convertirse en fricción. La discrepancia entre la segunda ley de la
termodinámica y la reversibilidad microscópica se plantea a partir de algo
tosco, las suposiciones para hacer el modelo hechas cuando se pasó de la
detallada descripción molecular a la estadística. Estas suposiciones
implícitamente especifican una flecha del tiempo, se permite que las
perturbaciones a gran escala se extingan bajo un plano perceptible a medida que
el tiempo avanza, pero no se permite a las perturbaciones a pequeña escala
seguir el escenario del tiempo reversible. Una vez la dinámica pasa a través de
esta trampilla temporal, no se permite que vuelva.
Si la entropía siempre aumenta, ¿cómo
la gallina jamás creó el huevo ordenado con el que empezar? Una explicación
común, avanzada por el físico austríaco Erwin Schrödinger en 1944 en un libro
breve y precioso llamado “¿Qué es la vida?”, es que los sistemas vivos de algún
modo toman prestado orden de su entorno y lo devuelven haciendo el entorno
incluso más desordenado de lo que de otro modo habría estado. Este orden extra
se corresponde a la «entropía negativa», que la gallina puede usar para hacer
un huevo sin violar la segunda ley. En un artículo posterior veremos que la
entropía negativa puede, en las circunstancias apropiadas, ser pensada como
información, y se reivindica con frecuencia que la gallina accede a la
información, proporcionada por su ADN, por ejemplo, para obtener la entropía
negativa necesaria. Sin embargo, la identificación de la información con
entropía negativa solo tiene sentido en unos contextos muy específicos, y las
actividades de las criaturas vivas no son uno de ellos. Los organismos crean
orden a través de procesos que llevan a cabo, pero estos procesos no son
termodinámicos. Las gallinas no acceden a algún almacén de orden para hacer que
las reglas de la termodinámica se equilibren, usan procesos para los cuales el
modelo termodinámico es inapropiado, y tiran las reglas porque no se aplican.
El escenario en el cual un huevo es
creado al tomar prestada entropía sería apropiado si el proceso que la gallina
usó era el inverso en el tiempo de un huevo rompiéndose en sus moléculas
constituyentes. A primera vista esto es plausible de un modo vago, porque las
moléculas que finalmente forman el huevo están esparcidas por todo el entorno;
se unen en la gallina, donde los procesos bioquímicos las ponen juntas de una
manera ordenada para formar un huevo. Sin embargo, hay una diferencia en las
condiciones iniciales. Si diste una vuelta de antemano etiquetando moléculas en
el entorno de la gallina, para decir «esta acabará en el huevo en tal o cual
localización», estarías a todos los efectos creando condiciones iniciales tan
complejas e improbables como las de hacer un huevo desrevuelto. Pero la gallina
no funciona así. Algunas moléculas podrían haber hecho el mismo trabajo: una
molécula de carbonato de calcio es tan buena para hacer la cáscara como
cualquier otra. De modo que la gallina no está creando orden del desorden. El
orden se asigna al resultado final del proceso de hacer el huevo, como barajar
las cartas en un orden aleatorio y luego numerarlas 1, 2, 3, etcétera, con un
rotulador. Sorprendente, ¡están en orden numérico!
Para estar seguro, el huevo parece más
ordenado que sus ingredientes, incluso si tenemos en cuenta esta diferencia en
las condiciones iniciales. Pero eso es porque el proceso que hace un huevo no
es termodinámico. De hecho, muchos procesos físicos hacen huevos desrevueltos.
Un ejemplo es el modo en que los minerales disueltos en agua puede crear
estalactitas y estalagmitas en las cuevas. Si especificamos la forma exacta de
la estalactita que queremos, por adelantado, estaríamos en la misma posición
que alguien tratando de recomponer un vaso roto. Pero si estamos dispuestos a
conformarnos con cualquier estalactita vieja, obtenemos una orden del desorden.
Estos dos términos son con frecuencia usados de una manera descuidada. Lo que
importa son qué tipo de orden y qué tipo de desorden.
Dicho esto, sigo sin esperar ver un
huevo desrevueltarse. No hay un modo factible de establecer las condiciones
iniciales necesarias. Lo mejor que podemos hacer es convertir el huevo revuelto
en comida para las gallinas y esperar que el ave ponga uno nuevo. De hecho, hay
una razón por la que no veríamos un huevo desrevueltarse, incluso si el mundo
fuese marcha atrás. Como nosotros y nuestras memorias somos parte del sistema
que está siendo invertido, no estaríamos seguros de qué sentido del tiempo está
«realmente» ocurriendo. Nuestro sentido del fluir del tiempo está producido por
las memorias, patrones psicoquímicos en el cerebro. En el lenguaje convencional,
el cerebro almacena registros del pasado, pero no del futuro. Imagina que haces
una serie de instantáneas del cerebro observando un huevo siendo revuelto,
junto con su memoria del proceso. En una etapa el cerebro recuerda un huevo
frío y que no estaba revuelto, y algo de su historia cuando lo cogimos del
frigorífico y lo pusimos en la sartén. En otra etapa recuerda haber batido el
huevo con un tenedor y haberlo movido de la nevera a la sartén.
Si ahora todo el universo gira al
revés, invertimos el orden en que las memorias ocurren en tiempo «real». Pero
no invertimos el orden de una memoria dada en el cerebro. Al principio (en el
tiempo invertido) del proceso que desrevuelve el huevo, el cerebro no recuerda
el «pasado» del huevo, cómo aparece de la boca en la cuchara, cómo fue
desbatido y cómo gradualmente construyó un huevo completo... En su lugar, el
registro en el cerebro en ese momento es uno en el que recuerda haber golpeado
un huevo para abrirlo, junto con el proceso de moverlo del frigorífico a la sartén
y hacerlo revuelto. Pero este recuerdo es exactamente el mismo que el de los
registros en el escenario en el que el tiempo va hacia delante. Lo mismo ocurre
para todas las otras instantáneas de la memoria. Nuestra percepción del mundo
depende de lo que observemos ahora, y qué memorias guarde nuestro cerebro
ahora. En un universo con un tiempo invertido, en realidad recordaríamos el
futuro, no el pasado.
La paradoja de la reversibilidad del
tiempo y la entropía no son problemas sobre el mundo real. Son problemas sobre
las suposiciones que hacemos cuando intentamos hacer un modelo de ellas.
© 2024 JAVIER DE LUCAS