BOSONES GAUGE

LOS BOSONES GAUGE

Antes de describir el mecanismo de Higgs, necesitamos primero investigar la ruptura espontánea de la simetría, un tipo especial de ruptura de la simetría que resulta central para aquél. La ruptura espontánea de la simetría desempeña un papel decisivo en muchas de las propiedades del universo que ya comprendemos y es muy posible que también lo haga en lo que sea que esté aún por descubrir. La ruptura espontánea de la simetría no es ubicua solamente en la física, sino que es, de hecho, una característica bien presente en la vida cotidiana. Una simetría rota espontáneamente es una simetría que se conserva por leyes físicas, pero no por el modo en las cosas están realmente dispuestas en el mundo. La ruptura espontánea de la simetría se produce cuando un sistema no puede preservar una simetría que de otro modo sí que estaría presente. Quizá la mejor manera de explicar cómo funciona esto es dar unos cuantos ejemplos.

Pensemos primero en una mesa circular dispuesta para la cena, alrededor de la cual se sientan una serie de personas que tienen vasos de agua colocados entre ellas. ¿Cuál es el vaso que debe uno usar, el que está colocado a su derecha o el que está colocado a su izquierda? No hay una respuesta óptima. Me dicen que la Sra. Buenas Maneras dice que ha de ser el colocado a la derecha, pero si dejamos de lado las arbitrarias reglas de la etiqueta, tanto da el vaso de la derecha como el de la izquierda. No obstante, en cuanto alguien escoge un vaso, se rompe la simetría. El ímpetu por elegir no habría de ser necesariamente parte del sistema; en este caso sería otro factor: la sed. Aun así, si alguien bebiera espontáneamente del vaso de la izquierda, lo mismo harían seguramente sus vecinos, y al final todo el mundo bebería del vaso de la izquierda.

La simetría existe hasta que alguien toma un vaso. En ese momento se rompe espontáneamente la simetría lateral entre izquierda y derecha. No hay ninguna ley de la física que dicte que alguien tenga que escoger la izquierda o la derecha. Pero uno tiene que escoger, y una vez hecho, la izquierda y la derecha ya no son iguales, en el sentido de que ya no hay una simetría que las intercambie.

He aquí otro ejemplo. Imaginemos un lápiz que está en posición vertical, apoyado sobre la punta, en el centro de un círculo. Durante el brevísimo segundo en el que está sobre la punta en posición exactamente vertical, todas las direcciones son equivalentes y existe una simetría rotacional. Pero un lápiz apoyado sobre su punta no puede estar mucho tiempo así: enseguida caerá espontáneamente en alguna dirección. Tan pronto como el lápiz se inclina, se rompe la simetría rotacional original. Obsérvese que no serían las leyes de la física mismas las que determinasen la dirección de caída. La física del lápiz que cae sería exactamente la misma, sea cual sea la dirección de caída. El que rompería la simetría sería el propio lápiz, el estado del sistema. Sencillamente, el lápiz no puede caer en todas las direcciones a la vez. Tiene que caer en una dirección determinada.

Parecería que una pared infinitamente larga y alta es igual en todos los puntos y a lo largo de todas las direcciones. Pero como una pared de verdad ha de tener límites, si queremos ver las simetrías debemos acercarnos a la pared hasta que los límites queden fuera del alcance de la vista. Los bordes de la pared nos dicen que no todo es igual a lo largo de la pared, pero si pegáramos la nariz a ella y viéramos solamente una pequeña porción suya, nos parecería que la simetría se conserva. Sería interesante pararse a pensar un rato este ejemplo, que muestra cómo puede dar la impresión de que una simetría se conserva cuando se la ve a una distancia, aunque parezca que se ha roto cuando se la ve desde otra: un concepto cuya importancia quedará patente enseguida.

En el mundo, casi todas las simetrías que sabríamos señalar no se conservan. Por ejemplo, hay muchas simetrías que estarían presentes en el espacio vacío, como la invarianza rotacional o traslacional, que nos dice que todas las direcciones y posiciones son la misma. Pero el espacio no está vacío: está salpicado de estructuras como las estrellas y el sistema solar, que ocupan posiciones determinadas y que están orientadas en direcciones determinadas que ya no conservan la simetría subyacente. Podrían estar en cualquier sitio, pero no pueden estar en todos los sitios. Las simetrías subyacentes tienen que romperse, aunque sigan implícitas en las leyes físicas que describen el mundo.

La simetría asociada con la fuerza débil también se rompe espontáneamente. En el resto de este capítulo explicaré cómo sabemos esto y discutiré algunas de sus consecuencias. Veremos que la ruptura espontánea de la simetría de la fuerza débil es la única manera de explicar la masa de las partículas y evitar a la vez las predicciones incorrectas para las partículas de altas energías que son inevitables en cualquier otra teoría candidata. El mecanismo de Higgs reconoce tanto la exigencia de la simetría interna asociada con la fuerza débil como la necesidad de que ésta se rompa.

El problema

La fuerza débil posee una propiedad especialmente extravagante. Al contrario que la fuerza electromagnética, que viaja largas distancias —propiedad de la que nos beneficiamos cada vez que encendemos la radio—, la fuerza débil sólo afecta a la materia que se encuentra a una distancia extremadamente corta. Dos partículas han de estar entre ellas a una distancia inferior a la diez mil billonésima parte de un centímetro para que puedan influenciarse mutuamente mediante la fuerza débil. Para los físicos que estudiaron la teoría cuántica de campos y la electrodinámica cuántica (QED, la teoría cuántica del electromagnetismo) en sus primeros tiempos, este rango de acción tan restringido era un misterio. La electrodinámica cuántica hacía pensar que las fuerzas —como la electromagnética, tan bien comprendida— tenían que transmitirse arbitrariamente lejos a partir de una fuente cargada. ¿Por qué la fuerza débil no se transmitía también a las partículas que estuvieran a cualquier distancia y no solamente a las que están tan próximas?

La teoría cuántica de campos, que combina los principios de la mecánica cuántica y la relatividad especial, dicta que si las partículas de baja energía transmiten fuerzas solamente a cortas distancias, entonces han de poseer masa; y cuanto más pesada sea la partícula, más corto será su radio de acción. Esto es una consecuencia del principio de incertidumbre y de la relatividad especial. El principio de incertidumbre nos dice que necesitamos partículas con un momento alto para sondear o influir en los procesos físicos a cortas distancias, y la relatividad especial vincula el momento a la masa. Aunque éste es un enunciado cualitativo, la teoría cuántica de campos precisa esta relación. Dice a qué distancia se desplazará la partícula con masa: cuanto más pequeña sea la masa, mayor será la distancia.

Por lo tanto, según la teoría cuántica de campos, el corto alcance de la fuerza débil solamente podía significar una cosa: los bosones gauge débiles que transmiten esta fuerza han de tener una cierta masa. Sin embargo, la teoría de las fuerzas funciona solamente para los bosones gauge como el fotón, que transmite una fuerza a largas distancias y que no tiene masa. Según la teoría original de las fuerzas, la existencia de masas no nulas era extraña y problemática: las predicciones de la teoría a altas energías cuando los bosones gauge tienen masa carecen de sentido. Por ejemplo, la teoría prevería que los bosones con mucha energía, con mucha masa, interactuarían entre sí con demasiada fuerza, con tanta fuerza, de hecho, que sería como si las partículas interactuasen más del cien por cien de las veces. Esta teoría simplista es claramente errónea.

Además, las masas de los bosones gauge débiles, los quarks y los leptones (todos los cuales, como sabemos, tienen una masa no nula) no conservan la simetría interna, que, como hemos visto es un ingrediente clave de la teoría de las fuerzas. Los físicos que tenían la esperanza de construir una teoría con partículas que tuvieran masa necesitaban obviamente una idea nueva. Los físicos han probado que el único modo de elaborar una teoría que evite las predicciones absurdas sobre los bosones gauge con masa y energía consiste en que se rompa espontáneamente la simetría de la fuerza débil a través del proceso que se conoce como mecanismo de Higgs. He aquí el porqué.

Una de las razones por las que queríamos incluir una simetría interna que eliminara una de las tres polarizaciones posibles de un bosón gauge era que una teoría sin la simetría hace el mismo tipo de predicciones absurdas que acabamos de mencionar. La teoría de fuerzas más sencilla sin una simetría interna predice que cualquier bosón gauge con energía, con o sin masa, interactúa con otros bosones gauge con una frecuencia excesiva. La teoría correcta de las fuerzas elimina este mal comportamiento en altas energías, vetando la polarización responsable de las predicciones incorrectas y que, de hecho, no existe en la naturaleza. Las polarizaciones espurias son la fuente de las predicciones problemáticas de la dispersión en alta energía, de modo que la simetría permite que queden sólo las polarizaciones físicas, las únicas que realmente existen y que son consistentes con la simetría. La simetría, que libra a la teoría de las polarizaciones no existentes, también elimina las predicciones incorrectas que, de otro modo, éstas producirían.

Esta idea funciona sólo, tal como está expuesta, para los bosones gauge sin masa. Los bosones gauge débiles, al contrario que el fotón, tienen masas no nulas. Los bosones gauge débiles viajan a una velocidad inferior a la de la luz. Y esto produce un tirón en el mecanismo. Mientras los bosones gauge sin masa tienen sólo dos polarizaciones que existen en la naturaleza, los bosones gauge con masa tienen tres. Una manera de comprender esta distinción es que los bosones gauge sin masa siempre viajan a la velocidad de la luz, lo que nos dice que no están nunca en reposo. Por lo tanto, siempre seleccionan una dirección de movimiento; así, podemos distinguir siempre las direcciones perpendiculares a la de la polarización restante, que oscila a lo largo de aquélla. Y resulta que para los bosones gauge sin masa, las polarizaciones físicas oscilan sólo en las dos direcciones perpendiculares.

Los bosones gauge con masa, sin embargo, son diferentes. Como todos los objetos familiares, pueden estar en reposo. Pero cuando un bosón con masa no se mueve, no selecciona ninguna dirección de movimiento. Para un bosón gauge con masa en reposo, las tres direcciones serían equivalentes. Pero si las tres direcciones son equivalentes, entonces deberían existir en la naturaleza las tres polarizaciones posibles. Y efectivamente existen. Aunque esta lógica nos parezca misteriosa, podemos descansar tranquilos, dado que los experimentadores han visto ya los efectos de esta tercera polarización de un bosón gauge con masa y han confirmado su existencia. La tercera polarización se llama polarización longitudinal. Cuando un bosón gauge con masa se mueve, la polarización longitudinal es la onda que oscila a lo largo de la dirección del movimiento; por ejemplo, la dirección de las oscilaciones de las ondas de sonido.

Esta polarización no existe en el caso de bosones gauge sin masa, como el fotón. Sin embargo, para los bosones gauge con masa, como los bosones gauge débiles, la tercera polarización es verdaderamente parte de la naturaleza. La tercera polarización ha de ser parte de la teoría del bosón gauge débil. Como esta tercera polarización es la fuente del radio de interacción a altas energías más grande de lo debido del bosón gauge débil, su existencia plantea un dilema. Ya sabemos que necesitamos una simetría para eliminar el mal comportamiento a alta energía. Pero esta simetría se libra de las predicciones incorrectas eliminando también la tercera polarización, y esa polarización es esencial para un bosón gauge con masa y, por lo tanto, para la teoría que lo describe. Aunque una simetría interna eliminaría las malas predicciones sobre el comportamiento a alta energía, lo haría a un precio demasiado alto: ¡la simetría se desembarazaría también de la masa!

El atolladero parece, a primera vista, insuperable, ya que los requerimientos de una teoría de los bosones gauge con masa parecen ser completamente contradictorios. Por una parte, no podría conservarse una simetría interna , ya que, de lo contrario, quedarían vetados los bosones gauge con masa con tres polarizaciones físicas. Por otra parte, sin una simetría interna para eliminar dos de las polarizaciones, la teoría de las fuerzas hace predicciones incorrectas cuando los bosones gauge tienen alta energía. Seguimos necesitando una simetría para eliminar la tercera polarización de cada bosón gauge con masa si queremos tener alguna esperanza de eliminar el mal comportamiento a alta energía.

La clave para resolver esta aparente paradoja y comprender la descripción cuántica correcta de un bosón gauge con masa era reconocer la diferencia entre los bosones con alta energía y los bosones con baja energía. En la teoría sin una simetría interna, solamente las predicciones sobre los bosones gauge de alta energía parecían problemáticas. Las predicciones sobre los bosones gauge con masa con baja energía eran sensatas (y ciertas). Estos dos hechos juntos implican algo bastante profundo: para evitar las predicciones problemáticas a altas energías, es esencial una simetría interna. Pero cuando los bosones gauge con masa tienen baja energía (baja comparada con la energía que la relación de Einstein E=mc² asocia con su masa), la simetría no debería conservarse. La simetría ha de ser eliminada para que los bosones gauge puedan tener masa y la tercera polarización pueda participar en las interacciones a baja energía en las que la masa marca una diferencia.

En 1964, Peter Higgs y otros descubrieron cómo las teorías de las fuerzas podrían incorporar a los bosones gauge con masa haciendo exactamente lo que acabamos de decir: manteniendo una simetría interna a altas energías, pero eliminándola a bajas energías. El mecanismo de Higgs, basado en la ruptura espontánea de la simetría, rompe la simetría interna de las interacciones débiles, pero sólo a baja energía. Esto asegura que la polarización extra estará presente a baja energía, donde la teoría la necesita. Pero la polarización extra no participará en los procesos a alta energía, y no aparecerán las interacciones sin sentido a altas energías.

Vamos a considerar ahora un modelo particular que rompe espontáneamente la simetría de la fuerza débil y que implementa el mecanismo de Higgs. Con este ejemplo del mecanismo de Higgs, veremos cómo adquieren masa las partículas elementales del modelo estándar.

El mecanismo de Higgs

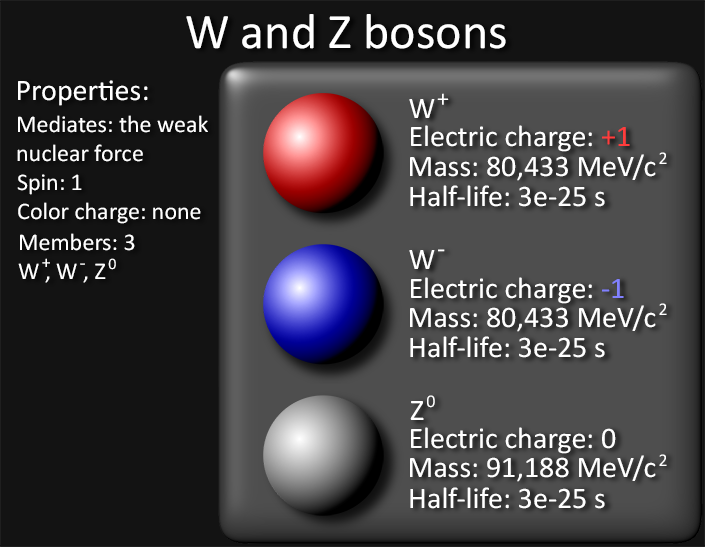
El mecanismo de Higgs implica un campo que los físicos llaman el campo de Higgs. Como hemos visto, los campos de la teoría cuántica de campos son objetos que pueden producir partículas en cualquier punto del espacio. Cada tipo de campo genera su propio tipo determinado de partícula. Un campo electrónico es una fuente de electrones, por ejemplo. Análogamente, un campo de Higgs es una fuente de partículas de Higgs. Como los quarks pesados y los leptones, las partículas de Higgs son tan pesadas que no se encuentran en la materia normal.

La naturaleza de la partícula de Higgs es uno de los asuntos sobre los cuales se discute más acaloradamente en la física de partículas. En esta sección, expondré el más sencillo de los muchos modelos que se presentan como candidatos —o sea, las posibles teorías que contienen diferentes fuerzas y partículas— y que muestra cómo funciona el mecanismo de Higgs. Independientemente de cómo resulte ser la auténtica teoría del campo de Higgs, ésta implementará el mecanismo de Higgs —la ruptura espontánea de la simetría de la fuerza débil y la concesión de masas a las partículas elementales— de la misma manera que el modelo que ahora mismo voy a presentar. En este modelo, un par de campos experimentan la fuerza débil. Más adelante resultará útil pensar que estos dos campos de Higgs, que están sujetos a la fuerza débil, son portadores de cargas de ésta. La terminología del mecanismo de Higgs es a veces poco rigurosa, ya que a veces el término Higgs se refiere a los dos campos juntos y otras veces a uno de los campos individuales (y a menudo también a las partículas de Higgs). Aquí distinguiré entre ambas posibilidades y me referiré a cada uno de los campos como Higgs1 y Higgs2.

Tanto Higgs1 como Higgs2 tienen capacidad de producir partículas. Pero también pueden asumir valores no nulos aunque no haya ninguna partícula presente. Hasta este momento no habíamos encontrado estos valores distintos de cero para un campo cuántico. De momento, aparte del campo eléctrico y el magnético, hemos considerado solamente campos cuánticos que crean o destruyen partículas, pero que toman el valor cero en ausencia de partículas. Pero los campos cuánticos pueden tener también valores no nulos, como los campos eléctrico y magnético clásicos. Y según el mecanismo de Higgs, uno de los campos de Higgs toma un valor no nulo. Ahora veremos que este valor no nulo es en esencia el origen de las masas de las partículas.

Cuando un campo toma un valor no nulo, el mejor modo de pensar en él es imaginar que el espacio manifiesta la carga que porta el campo, pero sin contener ninguna partícula de verdad. Habría que imaginarse que la carga que porta el campo está presente en todas partes. Es una pena, pero esta noción es muy abstracta porque el campo mismo es un objeto abstracto. Sin embargo, cuando el campo toma un valor no nulo, las consecuencias son concretas: la carga que porta un campo no nulo existe en el mundo real. Un campo de Higgs no nulo, en particular, distribuye la carga de la fuerza débil por todo el universo. Es como si el campo de Higgs que porta la fuerza débil pintara la carga de la fuerza débil por todo el espacio. Un valor no nulo de los campos de Higgs significa que la carga débil que porta Higgs1 (o Higgs2) está en todas partes, aunque no haya ninguna partícula presente. El mismo vacío, que es el estado del universo en el que no hay ninguna partícula presente, porta carga débil cuando uno de los dos campos de Higgs toma un valor no nulo.

Los bosones gauge débiles interactúan con esta carga débil del vacío, igual que lo hacen con cualquier otra carga débil. Y la carga que empapa el vacío bloquea a los bosones débiles cuando éstos tratan de comunicar fuerzas a largas distancias. Cuanto más lejos intentan llegar, más «pintura» encuentran. (Como la carga se extiende en realidad a lo largo de tres dimensiones, quizá sería preferible imaginarse una niebla de pintura). El campo de Higgs desempeña un papel muy parecido al de un agente de tráfico, restringiendo la influencia de la fuerza débil a distancias muy cortas. Cuando trata de comunicar la fuerza débil a partículas distantes, los bosones gauge portadores de la fuerza débil se topan con el campo de Higgs, que se interpone en su camino y los anula. Los bosones gauge débiles se mueven sin impedimentos sólo a una distancia muy corta, a la diez mil billonésima parte de un centímetro. Tanto los bosones gauge débiles pueden viajar libremente a distancias cortas, pero son interceptados a distancias más largas.

La carga débil en el vacío se encuentra dispersa de un modo tan sutil que en distancias cortas apenas hay rastro del campo de Higgs no nulo y la carga que éste lleva asociada. Los quarks, los leptones y los bosones gauge débiles viajan libremente a cortas distancias, casi como si no existiera la carga en el vacío. Los bosones gauge débiles pueden transmitir, por lo tanto, fuerzas a corta distancia, casi como si los dos campos de Higgs fueran cero. Sin embargo, a distancias más largas, las partículas viajan más lejos y se encuentran, por lo tanto, con una cantidad más significativa de carga débil. La cantidad exacta que encuentran depende de la densidad de carga, que depende a su vez del valor del campo de Higgs no nulo. El viaje (y la transmisión de la fuerza débil) a largas distancias no es posible para los bosones gauge débiles, pues en las excursiones largas la carga débil del vacío se interpone en su camino.

Esto es exactamente lo que necesitábamos para explicar el sentido de los bosones gauge débiles. La teoría cuántica de campos dice que las partículas que viajan libremente a distancias cortas, pero que sólo muy rara vez viajan a largas distancias, tienen masa no nula. Los viajes interrumpidos de los bosones gauge débiles nos dicen que éstos actúan como si tuvieran masa, ya que los bosones gauge con masa sencillamente no llegan muy lejos. La carga débil que empapa el espacio entorpece los viajes de los bosones gauge débiles, haciendo que se comporten exactamente como deberían hacerlo para concordar con lo que indican los experimentos.

Las cargas débiles en el vacío tienen una densidad que corresponde más o menos a las cargas que están separadas por una distancia de una diez mil billonésima de centímetro. Con esta densidad de carga débil, las masas de los bosones gauge débiles (los W cargados y el Z neutro) adoptan los valores que se han medido, de aproximadamente 100 GeV. Y esto no es todo lo que el mecanismo de Higgs logra. Es el responsable también de las masas de los quarks y de los leptones, las partículas elementales constituyentes de la materia en el modelo estándar. Los quarks y los leptones adquieren masa de un modo muy parecido al de los bosones gauge débiles. Los quarks y los leptones interactúan con el campo de Higgs que está distribuido por todo el espacio y resultan, por lo tanto, obstaculizados por la carga débil del universo. Como los bosones gauge débiles, los quarks y los leptones adquieren su masa absorbiendo la carga de Higgs que está distribuida por todas partes en el espacio-tiempo. Sin el campo de Higgs, estas partículas tendrían también masa nula. Pero, una vez más, el campo de Higgs no nulo y la carga débil del vacío interfieren con el movimiento y hacen que las partículas tengan masa. El mecanismo de Higgs es necesario también para que los quarks y los leptones adquieran su masa.

Aunque el mecanismo de Higgs constituye una explicación del origen de las masas más elaborado de lo que uno estimaría necesario, es el único modo práctico que tienen los bosones gauge débiles de adquirir masa, según la teoría cuántica de campos. La belleza del mecanismo de Higgs radica en que proporciona masa a los bosones gauge débiles, cumpliendo a la vez la tarea que expuse al principio de este capítulo. El mecanismo de Higgs hace que parezca que la simetría de la fuerza débil se conserva a distancias cortas (lo que, según la mecánica cuántica y la relatividad especial, es equivalente a altas energías) pero se rompe a largas distancias (equivalentes a bajas energías). Rompe espontáneamente la simetría de la fuerza débil, y esta ruptura espontánea está en la base de la solución del problema de la masa de los bosones gauge.

La ruptura espontánea de la simetría de la fuerza débil

Hemos visto que la transformación de simetría interna asociada a la fuerza débil intercambiará todo lo que esté cargado con la fuerza débil ya que la transformación de simetría actúa sobre todo aquello que interactúe con los bosones gauge débiles. Así pues, la simetría interna asociada a la fuerza débil ha de actuar sobre los campos Higgs1 y Higgs2, o sobre las partículas Higgs1 y Higgs2 que éstos crearían, y tratarlas como si fueran equivalentes, al igual que trata a los quarks up y down, que también experimentan la fuerza débil, como si fueran partículas intercambiables. Si los dos campos de Higgs fueran cero, serían equivalentes e intercambiables, y toda la simetría asociada a la fuerza débil se conservaría. Sin embargo, cuando uno de los dos campos de Higgs toma un valor no nulo, los campos de Higgs rompen espontáneamente la simetría de la fuerza débil. Si un campo es cero y el otro no, la simetría electrodébil, por la que Higgs1 y Higgs2 son intercambiables, se rompe.

Igual que la primera persona que escoge el vaso que tiene a su derecha o a su izquierda rompe la simetría entre izquierda y derecha en una mesa redonda, un campo de Higgs que tome un valor no nulo rompe la simetría de la fuerza débil que intercambia entre sí a los dos campos de Higgs. La simetría se rompe espontáneamente porque todo lo que rompe es el vacío, el estado real del sistema, el campo no nulo en este caso. No obstante, las leyes físicas, que permanecen inalterables, siguen conservando la simetría.

Una ilustración podría ayudar a transmitir cómo un campo no nulo rompe la simetría de la fuerza débil. La figura muestra una gráfica con dos ejes, etiquetados como eje x y eje y.

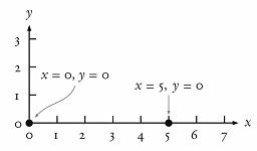
.Cuando se distingue el punto x = 0, y = 0, la simetría rotacional se conserva. Pero cuando se distingue x = 5, y = 0, se rompe la simetría rotacionalrotacional.

La equivalencia de los dos campos de Higgs es como la equivalencia de los ejes x e y sin ningún punto dibujado. Si girásemos la gráfica de modo que los ejes quedasen intercambiados, la gráfica seguiría presentando el mismo aspecto. Esto es consecuencia de la simetría rotacional usual. Obsérvese que si dibujo un punto en la posición x=0, y=0, esta simetría rotacional se conserva enteramente. Pero si pongo un punto que tenga una coordenada no nula, por ejemplo x=5 e y=0, la simetría rotacional ya no se conserva. Los dos ejes ya no son equivalentes pues el valor de x, pero no el valor de y, de este punto no es igual a cero. El mecanismo de Higgs rompe espontáneamente la simetría de la fuerza débil de un modo parecido. Cuando los dos campos de Higgs son cero, la simetría se conserva. Pero cuando uno es cero y el otro no, la simetría de la fuerza débil se rompe espontáneamente.

Las masas de los bosones gauge débiles nos dicen el valor preciso de la energía a la que se rompe espontáneamente la simetría de la fuerza débil. Esa energía es 250 GeV, la escala de la energía débil, muy próxima a las masas de los bosones gauge débiles, el W–, el W+ y el Z. Cuando las partículas tienen una energía superior a 250 GeV, la simetría se rompe y los bosones gauge débiles actúan como si tuvieran masa. Con el valor correcto del campo de Higgs no nulo, la simetría de la fuerza débil se rompe espontáneamente al valor correcto de la energía y los bosones gauge débiles adquieren la masa correcta.

Las transformaciones de simetría que actúan sobre los bosones gauge débiles actúan también sobre los quarks y los leptones. Y resulta que estas transformaciones no dejarán las cosas como antes a menos que los quarks y los leptones no tengan masa. Esto significa que las simetrías de la fuerza débil sólo se conservarían si los quarks y los leptones no tuvieran masa. Y como la simetría de la fuerza débil es esencial a altas energías, la ruptura espontánea de la simetría no sólo es precisa para las masas de los bosones gauge débiles, sino también para que los quarks y los leptones adquieran masa. El mecanismo de Higgs es el único camino para que las partículas fundamentales del modelo estándar adquieran su masa.

El mecanismo de Higgs funciona exactamente del modo preciso para asegurar que cualquier teoría que lo incorpore pueda tener bosones gauge débiles con masa (y también quarks y leptones con masa) y, sin embargo, haga las predicciones correctas sobre el comportamiento a altas energías. Concretamente, parece que la simetría se conserva para los bosones gauge débiles con alta energía (los que tienen una energía superior a 250 GeV), de modo que no hay predicciones incorrectas. A altas energías la simetría interna asociada con la fuerza débil sigue descartando la polarización problemática del bosón gauge débil, que causaría interacciones a un ritmo demasiado elevado. Pero a bajas energías, donde la masa es esencial para reproducir las interacciones a corta distancia de la fuerza débil medidas, la simetría de la fuerza débil se rompe.

Por esto es tan importante el mecanismo de Higgs. Ninguna otra teoría que asigne estas masas tiene estas propiedades. Otras posibles soluciones fallan a bajas a energías, donde la masa será incorrecta, o a altas energías, donde las interacciones se predecirán incorrectamente.

Gratificación

Hay un aspecto todavía más brillante del modelo estándar que no he explicado todavía. El mecanismo de Higgs nos ilumina sobre otras cosas, aparte de la fuerza débil. Sorprendentemente, también da ideas novedosas sobre el problema de por qué el electromagnetismo es tan especial. Hasta la década de 1960, nadie hubiera pensado que había todavía cosas por descubrir sobre la fuerza electromagnética, que había sido tan bien estudiada y comprendida durante más de un siglo. En la década de 1960, sin embargo, la teoría electrodébil que propusieron Sheldon Glashow, Steven Weinberg y Abdus Salam mostró que, cuando el universo comenzó su evolución a altas temperaturas y energías, había tres bosones gauge débiles y además un cuarto bosón neutro independiente, con una fuerza de interacción distinta. El fotón, ubicuo e importante como es hoy, no figuraba en esta lista. Los autores de la teoría electrodébil dedujeron la naturaleza del cuarto bosón gauge débil a partir de pistas físicas y matemáticas que no voy a describir aquí.

Lo notable es que el fotón originalmente no era nada especial. De hecho, el fotón del que hablamos hoy es realmente una mezcla de dos de los cuatro bosones gauge originales. La razón por la que el fotón resultó distinguido es que se trata del único bosón gauge que interviene en la fuerza electrodébil que es inmune a la carga débil del vacío. La principal propiedad característica del fotón es que éste viaja libre a través de la carga débil del vacío y que, por lo tanto, no tiene masa. El desplazamiento del fotón, al contrario que el del bosón W y Z, no es obstruido por el valor no nulo del campo de Higgs. Esto es así porque, aunque el vacío porta carga débil, no porta carga eléctrica. El fotón, que transmite la fuerza electromagnética, interactúa sólo con los objetos que tengan carga eléctrica. Por esta razón, el fotón puede transmitir fuerza a largas distancias sin interferencias del vacío. Es, por lo tanto, el único bosón gauge que sigue sin masa incluso en presencia de un campo de Higgs no nulo.

El fotón, esa cosa que los físicos pensaron durante años que entendían completamente, tiene un origen que sólo puede comprenderse en términos de una teoría más compleja que combina la fuerza débil y la fuerza electromagnética en una sola teoría. Esta teoría suele llamarse, consecuentemente, teoría electrodébil, y la simetría relevante correspondiente, simetría electrodébil. La teoría electrodébil y el mecanismo de Higgs son éxitos extraordinarios de la física de partículas. No sólo las masas de los bosones gauge débiles, sino también la relevancia del fotón quedan nítidamente explicadas dentro de este marco. Y por si esto fuera poco, nos permite comprender el origen de las masas de los quarks y de los leptones. Las ideas, bastante abstractas, que acabamos de encontrar, explican muy bien un abanico bastante amplio de propiedades de nuestro mundo.

Advertencia

El mecanismo de Higgs funciona magníficamente y proporciona a los quarks, a los leptones y a los bosones gauge débiles las masas que tienen, sin hacer predicciones sin sentido a altas energías, y además explican cómo surgió el fotón. Sin embargo, hay una propiedad esencial del mecanismo de Higgs que los físicos no comprenden todavía del todo. La simetría electrodébil debe romperse en torno a los 250 GeV para dar a las partículas las masas que se han medido. Los experimentos muestran que las partículas con una energía superior a 250 GeV no parecen tener masa, mientras que las partículas con una energía por debajo de 250 GeV actúan como si la tuvieran. Sin embargo, la simetría electrodébil se romperá a los 250 GeV sólo si la propia partícula de Higgs tuviera más o menos esta masa (valiéndose nuevamente de E=mc²); la teoría de la fuerza débil no funcionaría si la masa de Higgs fuera mucho mayor. Si la masa de Higgs fuera mayor, la ruptura de la simetría se produciría a una energía más alta y los bosones gauge débiles serían más pesados, contradiciendo así los resultados experimentales.

• Como tenemos que seguir prevenidos contra las predicciones falsas, la simetría de la fuerza débil tiene que conservarse, no obstante, a altas energías. Por lo tanto, la simetría de la fuerza débil ha de romperse sólo a energías bajas.

• La ruptura espontánea de la simetría se produce cuando todas las leyes físicas conservan una simetría, pero el sistema físico real no lo hace. Las simetrías rotas espontáneamente son simetrías que se conservan a altas energías, pero que se rompen a bajas energías. La simetría de la fuerza débil se rompe espontáneamente. • El proceso mediante el cual se rompe espontáneamente la simetría de la fuerza débil es el mecanismo de Higgs. Para que el mecanismo de Higgs rompa espontáneamente la simetría de la fuerza débil, tiene que haber una partícula con una masa aproximadamente igual a la masa de la escala débil, que es 250 GeV (recuérdese que la relatividad especial relaciona la masa y la energía mediante la fórmula famosa).

La gran unificación

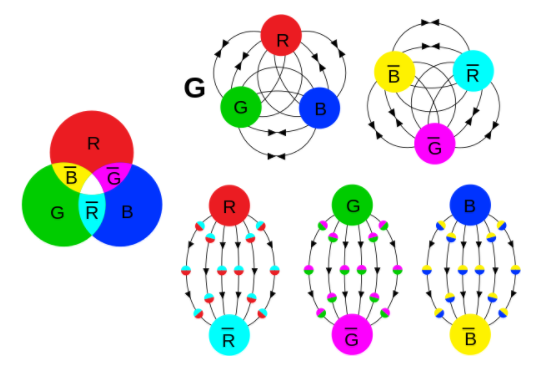
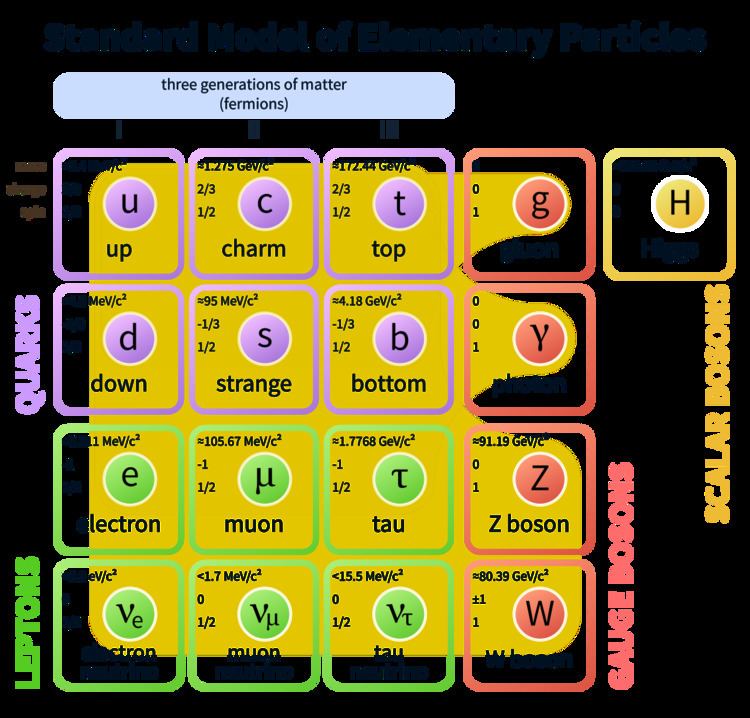
Los resultados de la sección anterior nos hablan de cómo dependen de la distancia las fuerzas fuerte, débil y electromagnética. En 1974, Georgi y Glashow insinuaron con atrevimiento que estas tres fuerzas cambian en función de la distancia y de la energía, de manera que resultan unificadas como una única fuerza a altas energías. A esta teoría la llamaron una gran teoría unificada (GUT, según sus siglas en inglés). Mientras que la simetría de la fuerza fuerte intercambia tres colores de quarks y la simetría de la fuerza débil intercambia diferentes parejas de partículas, la simetría de la fuerza de la GUT actúa sobre todos los tipos de partículas del modelo estándar, quarks y leptones, y los intercambia. Según la gran teoría unificada de Georgi y Glashow, en los primeros tiempos de la evolución del universo, cuando la temperatura y la energía eran enormemente altas —la temperatura era superior a los cien billones de billones de grados Kelvin y la energía superior a mil billones de GeV—, la intensidad de cada una de las tres fuerzas era la misma y las tres fuerzas no gravitatorias estaban fundidas en una única fuerza, «La Fuerza».

Al evolucionar el universo, la temperatura bajó y la fuerza unificada se escindió en tres fuerzas distintas, cada una con una dependencia diferente con respecto a la energía, a través de la cual evolucionaron hacia las tres fuerzas no gravitatorias que conocemos hoy. Aunque las fuerzas empezaron como una sola fuerza, acabaron con intensidades de interacción muy diferentes a bajas energías a causa de las distintas influencias que las partículas virtuales ejercieron sobre cada una de ellas. Las tres fuerzas serían como trillizos idénticos que se desarrollaran a partir de un único huevo fertilizado, pero que maduraran para producir tres individuos bastante diferentes. Uno de los trillizos podría ser ahora un cantante punk con una cresta de pelo teñido, otro un marine con el pelo rapado y el tercero un artista con una larga coleta. Compartirían, de todos modos, el mismo ADN y, de bebés, habrían sido casi indistinguibles.

En los primeros tiempos del universo, las tres fuerzas habrían sido también indistinguibles. Pero luego se habrían diferenciado mediante la ruptura espontánea de la simetría. Así como el mecanismo de Higgs rompió la simetría electrodébil y sólo dejó intacto el electromagnetismo, rompería también la simetría de la GUT y dejaría las tres fuerzas independientes que vemos hoy. Una única intensidad de interacción a altas energías es un prerrequisito para una gran teoría unificada. Esto implica que las tres líneas que representan la intensidad de interacción como función de la energía deben coincidir a partir de un valor dado de la energía. Pero ya sabemos cómo varía la intensidad de las tres fuerzas no gravitatorias en función de la energía. Y como la mecánica cuántica nos dice que una distancia larga equivale a una energía baja y que una distancia corta equivale a una energía alta, los resultados de la sección anterior pueden interpretarse igualmente en términos de la energía. A bajas energías, las fuerzas electromagnética y débil son menos potentes que la fuerza fuerte, pero se intensifican a energías más altas, mientras que la fuerza fuerte se debilita.

En otras palabras, las intensidades de las tres fuerzas no gravitatorias se van haciendo más equiparables a energías más altas. Podrían incluso converger hacia una intensidad común. Esto significaría que las tres líneas que representan la intensidad de interacción en función de la energía coinciden a altas energías. Dos líneas que se encuentran en un punto no es un resultado tan fascinante: eso va a ocurrir de todos modos si las dos líneas se van aproximando. Pero que tres líneas se encuentren en un punto es una gran coincidencia o la prueba de algo más significativo. Si es verdad que las fuerzas convergen, su intensidad de interacción común podría ser una indicación de que hay sólo un único tipo de fuerza a altas energías, y en ese caso tendríamos una teoría unificada.

Aunque la unificación sigue siendo hasta hoy una conjetura, la unificación de las fuerzas, si fuera cierta, sería un gran salto hacia una descripción más sencilla de la naturaleza. Al ser los principios de unificación tan intrigantes, los físicos estudiaron la intensidad de las tres fuerzas a altas energías para ver si convergen o no. Hacia 1974, nadie había calculado la intensidad de interacción de las tres fuerzas no gravitatorias con una gran precisión. Howard Georgi, Steven Weinberg y Helen Quinn (por aquel entonces, ayudante postdoctoral sin sueldo en Harvard, y, actualmente, física de plantilla en el Acelerador Lineal de Stanford y presidenta de la Sociedad Americana de Física) usaron las mediciones imperfectas que estaban entonces disponibles e hicieron un cálculo con el grupo de renormalización para extrapolar la intensidad de las fuerzas a altas energías. Descubrieron que las tres líneas que representan la intensidad de las fuerzas no gravitatorias parecían realmente convergir en un único punto.

El famoso artículo de Georgi y Glashow de 1974 sobre su teoría de la gran unificación comienza con estas palabras: «Presentamos una serie de hipótesis y de especulaciones que conducen sin remedio a la conclusión […] de que todas las fuerzas producidas por partículas elementales (la fuerte, la débil y la electromagnética) son diferentes manifestaciones de la misma interacción fundamental que involucra a una única intensidad de conexión. Nuestras hipótesis pueden ser erróneas y nuestras especulaciones absurdas, pero la unidad y la sencillez de nuestro esquema son razones suficientes para que sea tomado en serio». Quizá aquellas palabras no eran demasiado modestas. Sin embargo, Georgi y Glashow no pensaban realmente que la unidad y la sencillez constituyeran pruebas suficientes de que su teoría fuera una descripción correcta de la naturaleza. También querían que hubiera una confirmación experimental.

Aunque era preciso un tremendo acto de fe para extrapolar el modelo estándar a una energía diez billones de veces más grande que la que había sido explorada directamente hasta entonces, se dieron cuenta de que esa extrapolación tenía una consecuencia verificable. En su artículo, Georgi y Glashow explicaron que su GUT, su teoría de la gran unificación, «predice que el protón se desintegra» y que los físicos experimentales deberían intentar comprobar esta predicción. La teoría unificada de Georgi y Glashow predecía que los protones no durarían siempre. Después de mucho tiempo, se desintegrarían. Esto no pasaría nunca en el modelo estándar. Los quarks y los leptones se distinguen normalmente entre sí por las fuerzas que experimentan. Pero en una gran teoría unificada, las fuerzas son todas esencialmente una misma fuerza. Así, al igual que un quark up puede convertirse en un quark down por efecto de la fuerza débil, un quark podría convertirse en un leptón por efecto de la fuerza unificada. Esto implica que, si la idea de la gran teoría unificada es correcta, el número total de quarks del universo no sería fijo y un quark podría convertirse en un leptón, haciendo que el protón, que está compuesto de tres quarks, se desintegre.

Como el protón puede desintegrarse en una gran teoría unificada que vincula los quarks a los leptones, toda la materia familiar sería, en definitiva, inestable. Sin embargo, la tasa de desintegración del protón es lentísima: su tiempo de vida superaría ampliamente la edad del universo. Esto implica que la señal de un protón que se desintegra, por vistosa que sea, tiene poquísimas posibilidades de ser detectada, ya que se produce muy rara vez. Para encontrar pruebas de la desintegración del protón, los físicos tuvieron que diseñar experimentos en extremo complicados y de larga duración, que estudiaron una enorme cantidad de protones. De este modo, aunque es muy poco probable que cualquier protón concreto se desintegre, un gran número de protones incrementa mucho la posibilidad de que el experimento pueda detectar la desintegración de uno de ellos. Aunque la probabilidad de que nos toque la lotería es pequeña, sería mucho mayor si compráramos millones de billetes.

Los físicos diseñaron ciertamente este tipo de experimentos, complicados y a base de muchos protones; entre ellos está el proyecto Irvine/Michigan/Brookhaven (IMB), localizado en la mina Homestake, en Dakota del Sur, y el proyecto Kamiokande, una tina de agua y de detectores enterrados a un kilómetro de profundidad en Kamioka, Japón. Aunque la desintegración del protón es un proceso rarísimo, estos experimentos ya hubieran encontrado pruebas de él si la teoría de la gran unificación de Georgi y Glashow fuera correcta. Por desgracia para las ambiciones de la gran unificación, nadie ha descubierto hasta ahora esa desintegración.

Esto no descarta necesariamente la unificación. De hecho, gracias a medidas más precisas de las fuerzas, ahora sabemos que el modelo original propuesto por Georgi y Glashow es, casi con certeza, incorrecto, y que sólo una versión ampliada del modelo estándar puede unificar las fuerzas. Resulta que en esos modelos las predicciones sobre la vida del protón son más largas y por eso resultaría lógico que la desintegración del protón no haya sido detectada aún. Todavía hoy no sabemos realmente si la unificación de las fuerzas es una verdadera propiedad de la naturaleza, y si es así, qué significa eso. Los cálculos muestran que la unificación podría darse en varios modelos, entre los que se encuentran los modelos supersimétricos, los modelos extradimensionales de Horava y Witten y los modelos extradimensionales arqueados que desarrollarom Raman Sundrum y Randall. Los modelos extradimensionales son particularmente intrigantes porque podrían llevar a la gravedad al redil de la unificación y unificar de verdad las cuatro fuerzas conocidas. Estos modelos son también importantes porque en los modelos originales de unificación se suponía que no había nuevas partículas por descubrir que estuvieran por encima de la escala débil y que no fueran las que tienen masa en la escala de la teoría de la gran unificación.

Estos otros modelos demuestran que la unificación podría darse aunque hubiera muchas otras partículas que pudieran producirse solamente a energías que están por encima de la escala débil. Sin embargo, por fascinante que pueda ser la unificación de las fuerzas, los físicos se encuentran actualmente divididos sobre sus méritos teóricos, según propugnen un planteamiento de la física que vaya de arriba hacia abajo o uno que vaya de abajo hacia arriba. La idea de una teoría de la gran unificación encarna el planteamiento que va de arriba hacia abajo. Georgi y Glashow formularon una atrevida hipótesis sobre la ausencia de partículas con masa entre mil y mil billones de GeV y desarrollaron una teoría hipotética basada en esta suposición. La gran unificación fue el primer paso del debate de la física de partículas que continúa hoy con la teoría de cuerdas. Ambas teorías extrapolan las leyes físicas desde las energías efectivamente medidas hasta energías por lo menos diez billones de veces superiores.

Georgi y Glashow se volvieron después escépticos sobre el planteamiento que va de arriba hacia abajo, que está representado por la teoría de cuerdas y por la búsqueda de la gran unificación. Desde entonces han vuelto sobre sus pasos y ahora se concentran en la física de bajas energías. Aunque las teorías unificadas tienen algunos rasgos atractivos, no estoy realmente seguro de que con su estudio se llegará a ideas correctas sobre la naturaleza. El intervalo de energías que hay entre lo que sabemos y lo que extrapolamos es enorme, y podemos imaginar muchas posibilidades para lo que puede ocurrir a medio camino. En todo caso, hasta que se descubra la desintegración del protón (o alguna otra predicción), si es que esto ocurre alguna vez, será imposible establecer con certeza si las fuerzas de verdad se unifican a altas energías. Hasta entonces, esta teoría permanecerá en el reino de las especulaciones grandiosas, pero teóricas.

LO QUE HAY QUE RECORDAR:

• Las partículas virtuales son partículas que tienen la misma carga que las auténticas partículas físicas, pero que tienen energía que parece ser incorrecta.

• Las partículas virtuales existen sólo durante un breve lapso de tiempo; temporalmente, toman prestada energía del vacío, el estado del universo en el que no hay ninguna partícula.

• Las contribuciones cuánticas a los procesos físicos surgen de las partículas virtuales que interactúan con las partículas reales. Estas contribuciones de las partículas virtuales influyen en las interacciones de las partículas reales, apareciendo y desapareciendo, y actuando como intermediarias entre las partículas reales.

• El principio de anarquía nos dice que cuando se consideran las propiedades de una partícula, las contribuciones cuánticas han de tenerse siempre en cuenta.

• En una teoría unificada, una única fuerza de alta energía se convierte a bajas energías en las tres fuerzas conocidas que son distintas de la gravedad. Para que las tres fuerzas se unifiquen, han de tener la misma intensidad a altas energías.