LA CUARTA DIMENSION

Al echar un vistazo a nuestro alrededor podemos observar un mundo tridimensional: los objetos están formados por las tres dimensiones espaciales usuales. Aunque todos conocemos que estos objetos se mueven en el tiempo solemos asignar a este último una realidad independiente de los objetos tridimensionales. Sin embargo, una vez más, la realidad parece superar a la ficción: nuestro Universo real posee cuatro dimensiones y como veremos en este artículo estas dimensiones están estrechamente conectadas entre sí. En este artículo visualizaremos nuestro Universo cuatridimensional y veremos cuáles son sus efectos medibles. Como si viviéramos en la cueva de Platón nosotros solo vemos las sombras tridimensionales de objetos que se mueven en un Universo cuatridimensional, lo cual nos lleva a interpretar esas "sombras" como fenómenos extraños y "exóticos".

¡Bienvenidos a nuestro extraño mundo cuatridimensional!

Visualizando la cuarta dimensión

Consideremos un objeto cotidiano como una escalera de 4 metros. Esta escalera se encuentra en reposo con respecto a un observador, al que llamaré Javier, y posee dos relojes sincronizados en ambos extremos. En un momento dado Javier se sitúa justo en medio de la escalera y mide la distancia entre ambos extremos en el mismo instante de tiempo (para Javier los relojes de ambos extremos marcan el mismo tiempo). La longitud medida es por supuesto de 4 metros. A continuación comenzaremos a ver las "sombras" de los objetos moviéndose en cuatro dimensiones: consideremos la escena anterior vista desde una observadora, a la que llamaré Estrella, que pasa justo encima de la escalera en un cohete que viaja al 60% de la velocidad de la luz. Desde el sistema de referencia de Estrella la nave está en reposo y es la escalera la que se acerca al 60% de la velocidad de la luz. Cuando la escalera llega a la nave y Estrella observa a Javier haciendo la medición, esta nota algo "sorprendente": desde su sistema de referencia ¡Javier no mide ambos extremos al mismo tiempo! Primero mide el extremo anterior y después el extremo posterior. Por otro lado, el sensor de medición de la nave que se activa justo cuando el extremo anterior de la escalera, se encuentra a la altura del morro de la nave y se desactiva justo cuando el extremo posterior de la escalera ha traspasado dicho sensor, arroja una medida de ¡3.2 metros! (1). Posteriormente, cuando ambos se encuentran en la cafetería, Javier le dice a Estrella que la escalera mide 4 metros pero ella insiste que la medida real son 3.2 metros. Además Estrella le dice a Javier que él no ha realizado la medida al mismo tiempo, mientras que Javier insiste en que es ella la que no ha realizado la medida en el mismo instante. ¿Qué demonios está pasando aquí? ¿Quién de los dos tiene razón? Para tratar de entender lo que está pasando dibujaremos el diagrama espacio-temporal de la escena anterior.

Un sistema de referencia S´que se mueve a una velocidad V con respecto a un sistema en reposo S se representaría de la siguiente forma:

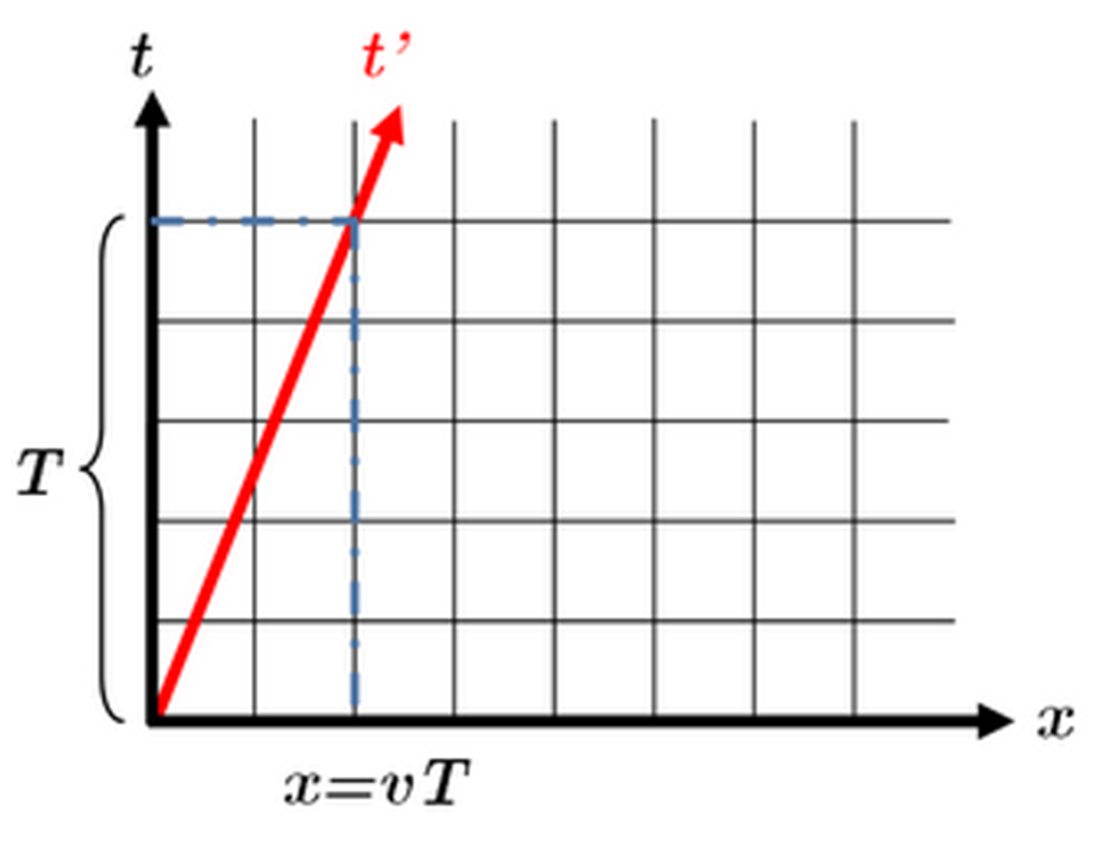
El eje vertical representa el tiempo y el eje horizontal el espacio. El sistema S en reposo solo se mueve en el tiempo y recorre un intervalo T mientras que el sistema S´en ese intervalo T se ha movido también en el espacio una distancia vT. De esta forma observamos una característica fundamental de los diagramas espacio-temporales: el sistema en movimiento posee los ejes inclinados con respecto al sistema en reposo:

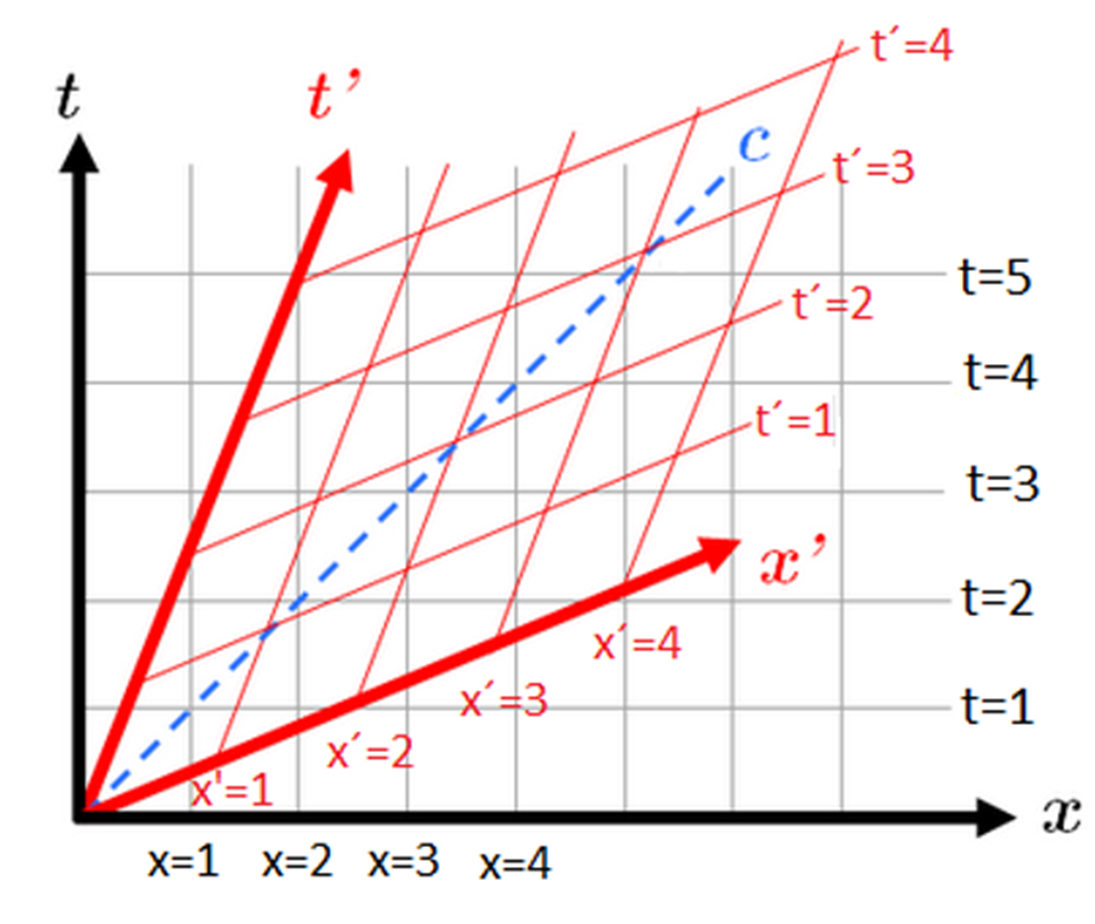
El eje x´representa el instante t´=0 en el sistema de referencia en movimiento. Los sucesivos instantes de tiempo t´=1, t´=2 etc. se representan con líneas paralelas al

eje x´. De la misma forma las distancias x´=1, x´=2 etc. se representan con líneas paralelas al eje t´. En el sistema de referencia en reposo S las líneas espaciales y temporales se representan de la forma usual paralelas a los ejes x y t.

Como los ejes están inclinados en el sistema de referencia S´, las líneas de simultaneidad de ambos sistemas son diferentes, es decir, eventos que son simultáneos en S no son simultáneos en S´y viceversa:

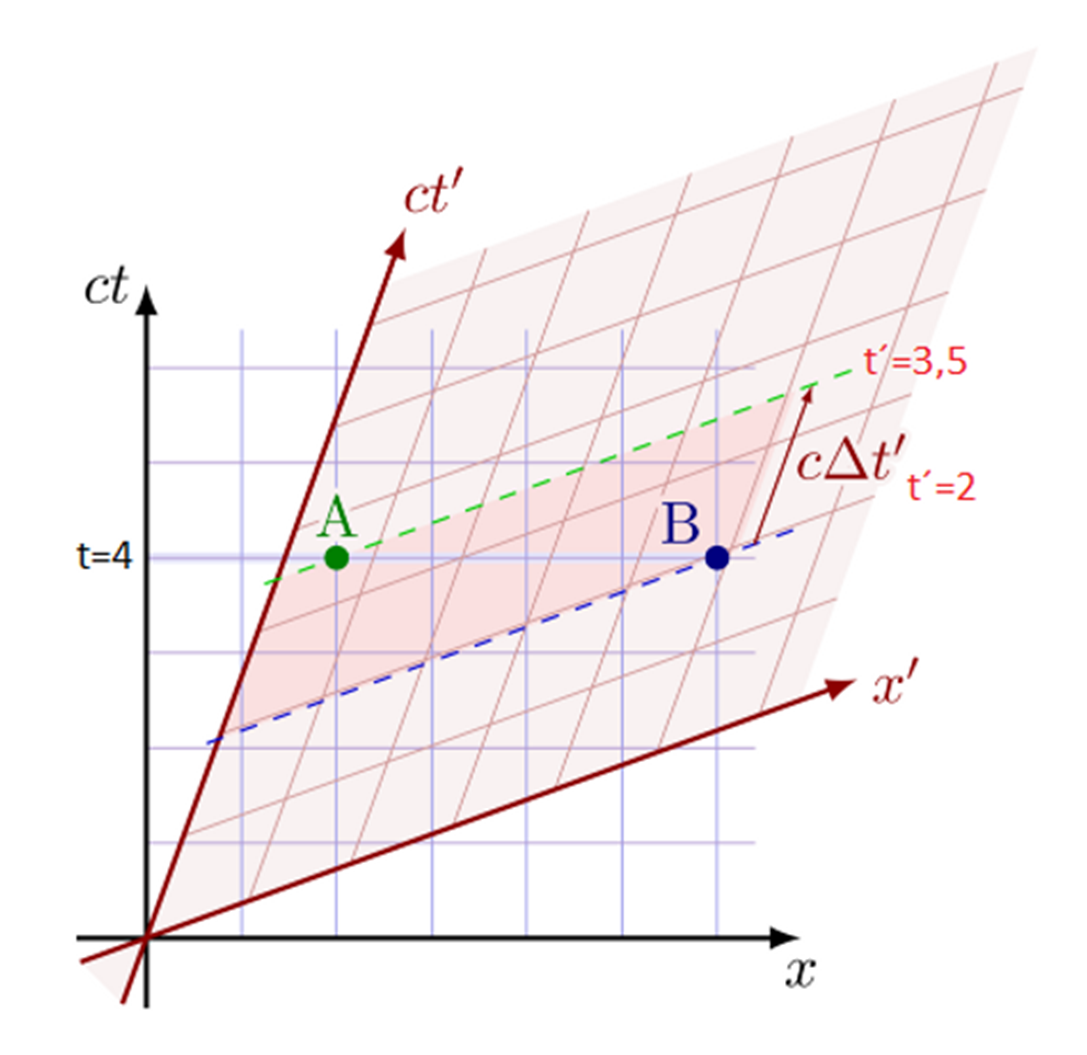
Los eventos A y B ocurren en el mismo instante en el sistema de referencia en reposo S (instante t=4) pero en el sistema de referencia en movimiento S´primero ocurre el evento B (instante t´=2) y después el evento A (instante t´=3.5)

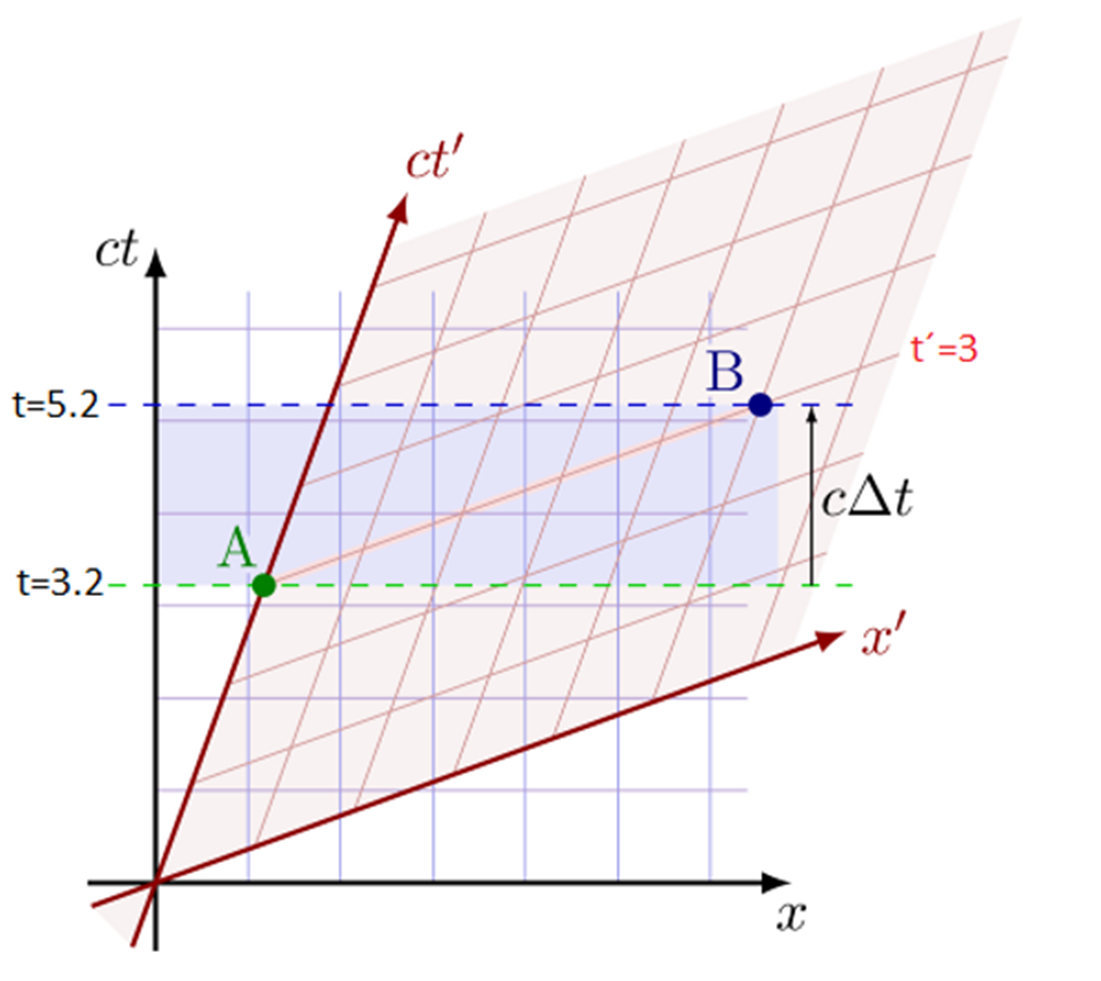
Los eventos A y B ocurren a la vez en el sistema de referencia S´(instante t´=3) pero no son simultáneos en S (primero ocurre A en t=3.2 y luego ocurre B en t=5.2).Ahora ya estamos en disposición de visualizar la cuarta dimensión superponiendo ambos sistemas de referencia:

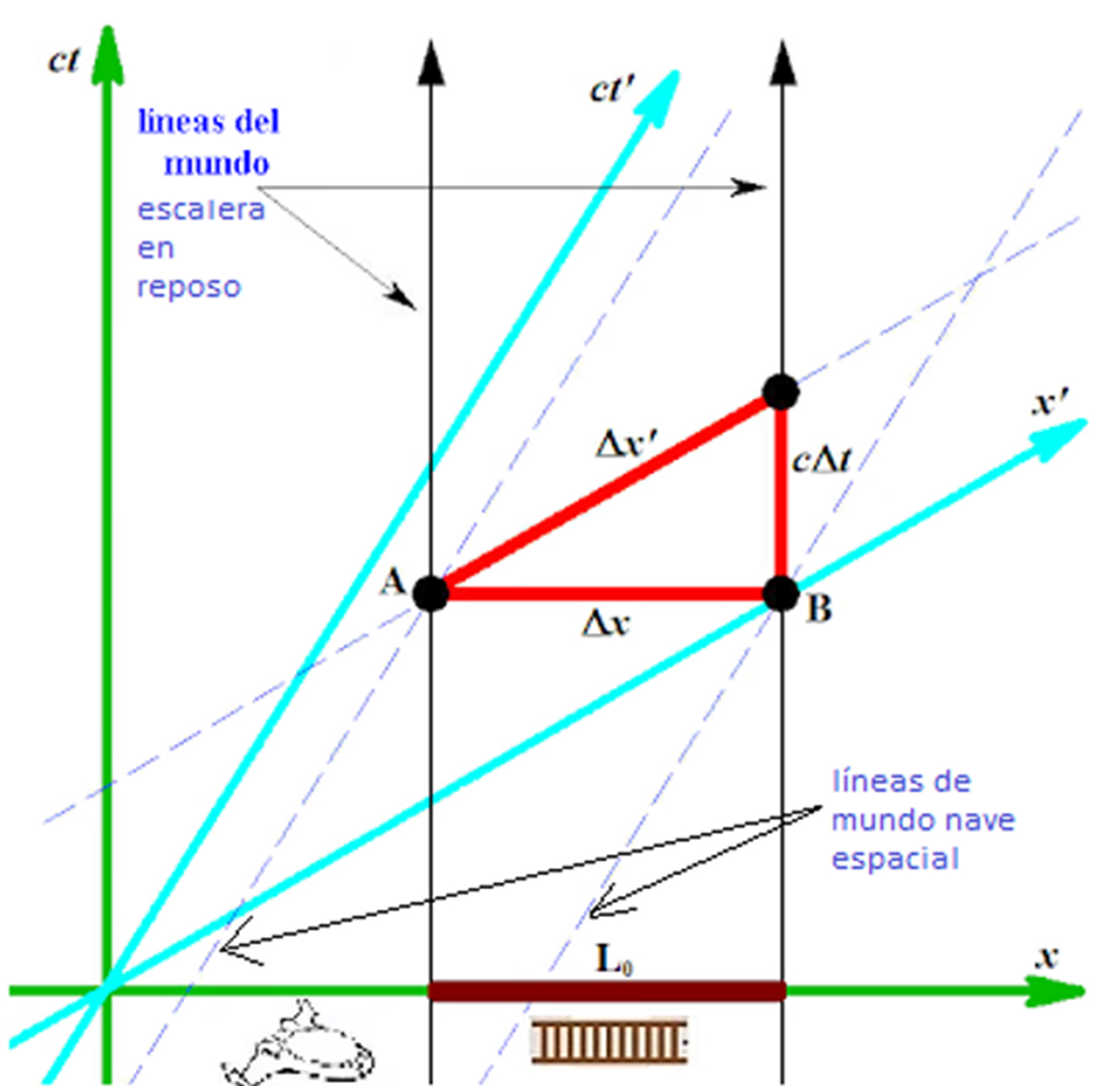
Las líneas negras verticales representan el movimiento de los extremos de la escalera en reposo de longitud Lo. Las líneas inclinadas discontinuas representan los extremos de la nave espacial en movimiento. Los eventos A y B son los puntos del espacio-tiempo donde coinciden los extremos de la escalera con los extremos de la nave espacial (puede apreciarse en la figura que es donde ambas "líneas de mundo" se cortan). El punto clave es el siguiente: para Javier las líneas de simultaneidad son horizontales y por tanto la longitud medida en el mismo instante es delta-x (longitud Lo); sin embargo, para Estrella las líneas de simultaneidad están inclinadas y por tanto la medición realizada en un cierto instante de tiempo es la longitud delta-x´.

Si graduamos los dos ejes podemos apreciar las magnitudes medidas por ambos observadores:

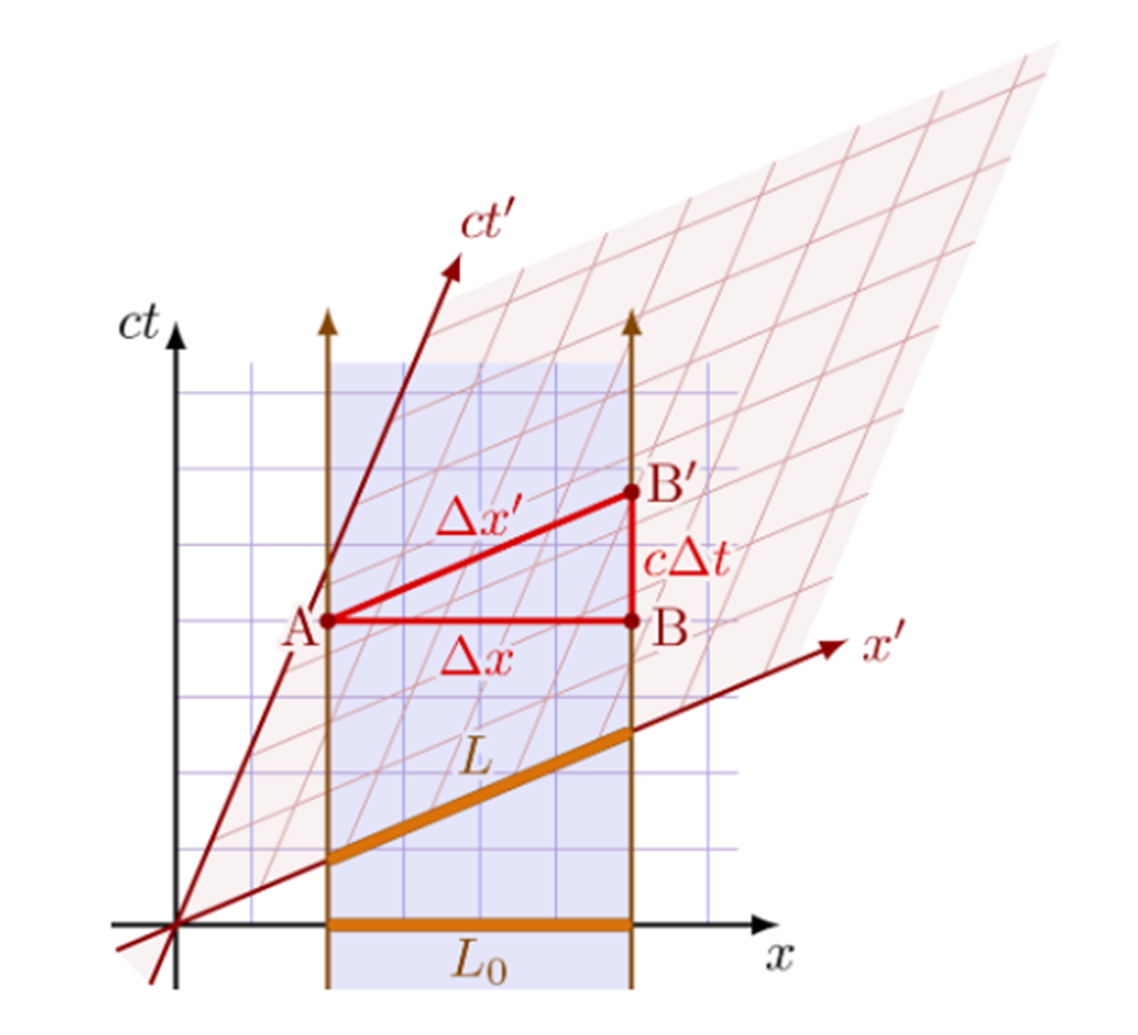
Como podemos observar en el diagrama, la longitud Lo en S es de 4 metros mientras que la longitud L en S´es de solo 3,2m (2). Además, mientras que para Javier los eventos A y B son simultáneos para Estrella no lo son, para ella los eventos simultáneos son los eventos A y B´. Sin embargo, para Javier, el intervalo A-B´no solo tiene unidades de longitud sino que también posee unidades de tiempo es decir, posee una mezcla de magnitudes espaciales y temporales. ¡Acabamos de visualizar la cuarta dimensión de un objeto tridimensional que se mueve en un mundo cuatridimensional!

Ahora estamos en disposición de entender que es lo que está sucediendo en realidad: las líneas de mundo que hemos dibujado en los diagramas anteriores están dibujadas en un espacio-tiempo cuatridimensional y diferentes observadores miden diferentes "cortes" tridimensionales de un mismo objeto cuatridimensional. Estos cortes tienen diferentes valores de espacio y de tiempo: lo que para un observador es espacio para otro es tiempo y viceversa. ¡La realidad tiene 4 dimensiones, pero nosotros, como seres tridimensionales, solo podemos detectar las sombras tridimensionales! ¿No es esto realmente increíble?

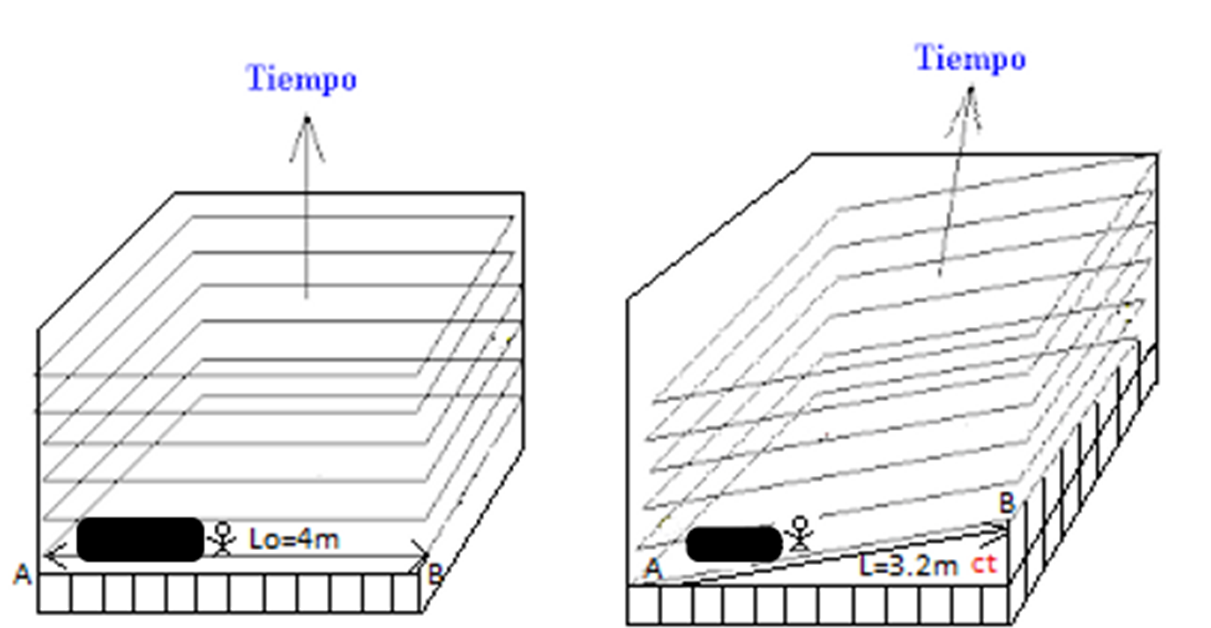
En la figura de la izquierda, Javier, en reposo frente a la escalera mide "rodajas horizontales" de la escalera; para él, los eventos A y B correspondientes a los extremos de la escalera son simultáneos y por tanto detecta una longitud Lo=4m. En la figura de la derecha, Estrella experimenta un factor de Lorentz de 1.25 ya que viaja al 60% de la velocidad de la luz con respecto a la escalera. Estrella mide "rodajas" inclinadas de la escalera y los eventos A y B no son simultáneos: primero mide el extremo A y luego el extremo B. Para Javier ¡Estrella está midiendo una mezcla de intervalos espaciales y temporales!

El salto desde la Relatividad Especial a la Relatividad General

Imaginemos el siguiente experimento mental: una persona se encuentra montada en un carrusel cuyo giro se está acelerando. Fuera del mismo, en reposo, se colocan dos esferas metálicas separadas 10 metros de distancia. Cada vez que el carrusel da una vuelta completa el observador abre los ojos y observa las esferas. En la primera vuelta el tiovivo apenas ha acelerado y por tanto el observador ve las dos esferas separadas 10 metros de distancia. En la segunda vuelta el carrusel ya viaja a 0.5c y por tanto el observador detectará que las esferas están más cerca debido a la contracción de longitud relativista. En la tercera vuelta la velocidad es ya de 0.8c y por tanto las esferas se verán más cerca todavía. Con la cuarta vuelta a 0.9c el proceso de "acercamiento" de las esferas continua:

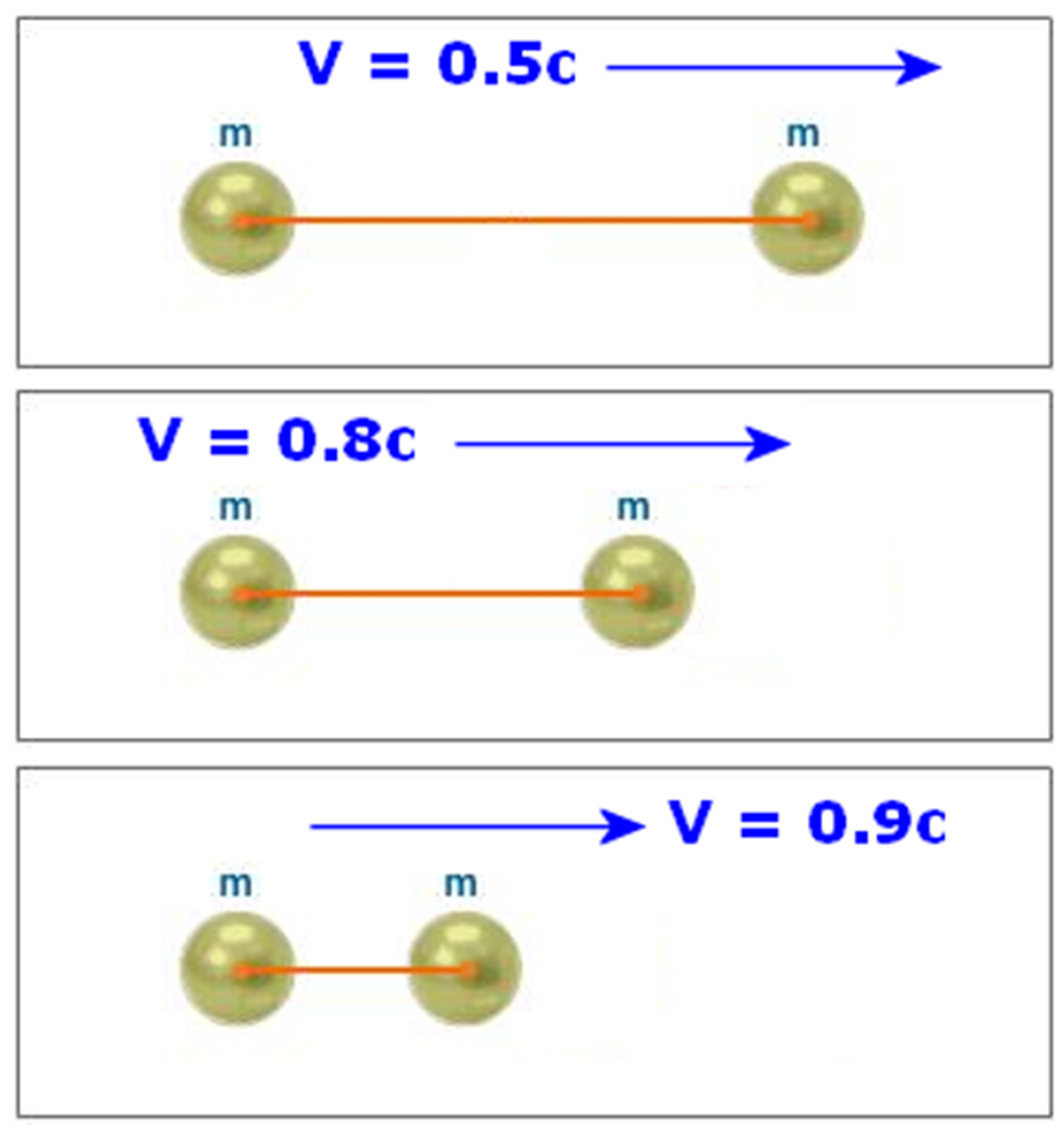
Si la aceleración del carrusel no es constante, sino variable, entonces el observador verá que las dos masas se aceleran una hacia la otra. Este efecto implica que los objetos medidos en un marco de referencia acelerado se detectarán como atrayéndose unos a otros debido a que la distancia entre ellos se está acortando por los efectos relativistas. Einstein se dio cuenta de que un observador dentro de una caja metálica que acelera en el espacio no podría distinguir desde dentro si la caja se está acelerando o si está inmersa en un campo gravitatorio. Esta idea constituye uno de los pilares fundamentales de la relatividad general: no existe una fuerza de atracción entre los objetos masivos, es el propio espacio existente entre ellos el que se está comprimiendo:

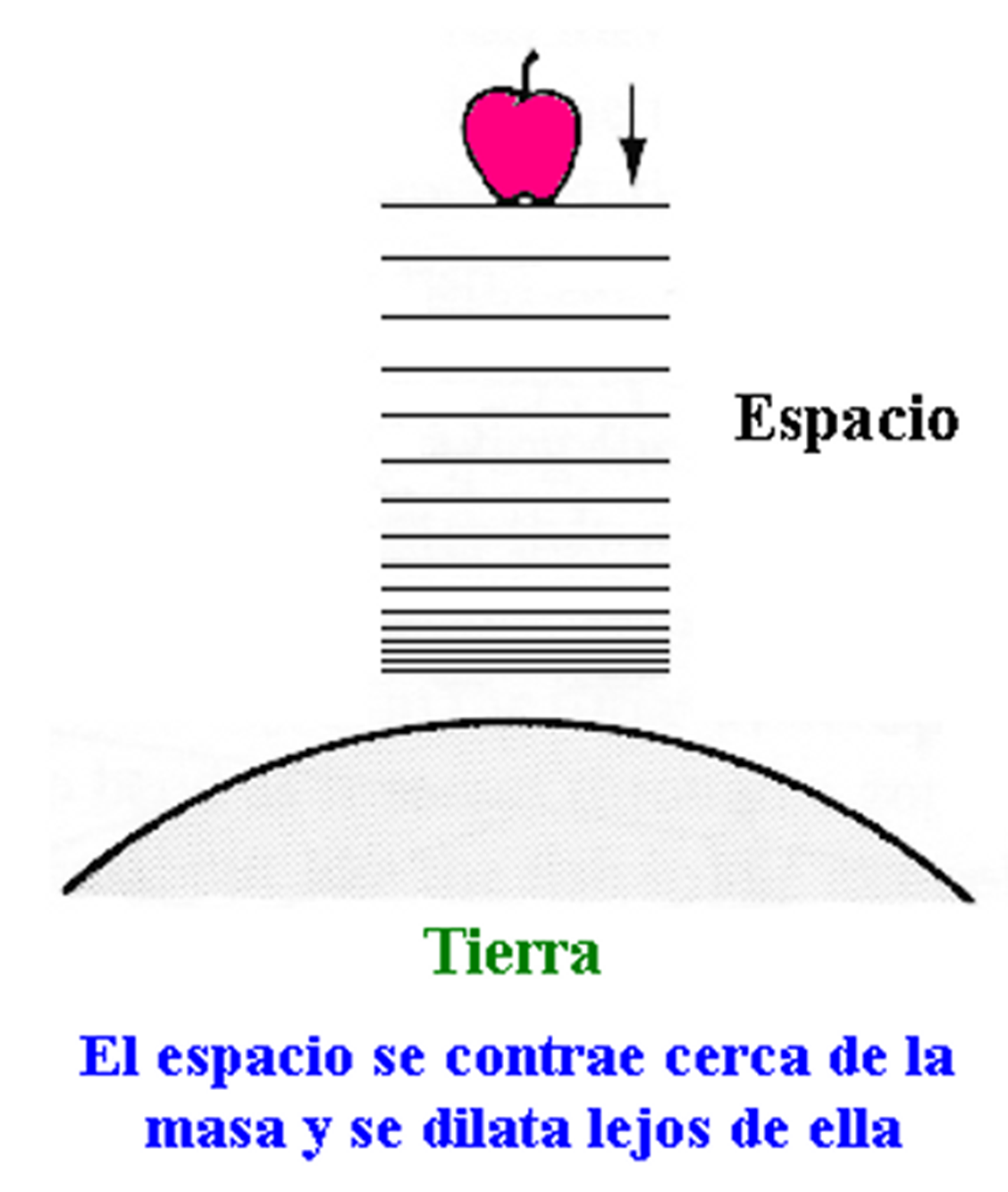
La visión que acabamos de dar es solo intuitiva ya que no es solo el espacio el que se comprime sino que el tiempo también se dilata:

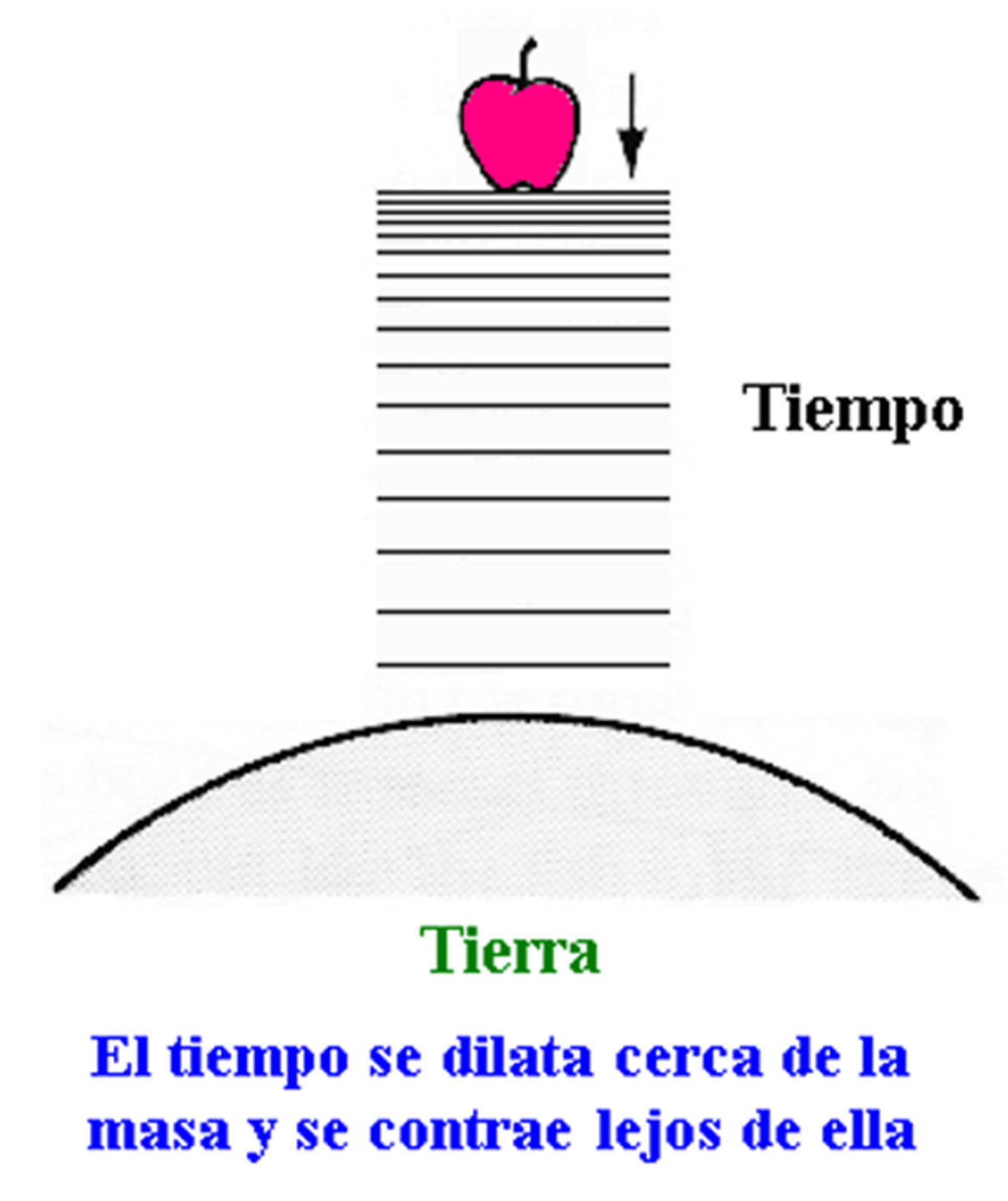
Por tanto, este proceso no se produce solo en el espacio 3D sino en el espacio-tiempo cuatridimensional. En la relatividad general la existencia de un espacio-tiempo de cuatro dimensiones se hace incluso más evidente que en la relatividad especial: ahora la gravedad es (localmente) equivalente a un marco de referencia acelerado y los cuerpos siguen trayectorias (geodésicas) en un espacio-tiempo curvo de 4 dimensiones. La Tierra sigue una geodésica a través del espacio-tiempo 4D curvado que produce la gravedad del Sol.

No es difícil de imaginar el asombro y la perplejidad de la comunidad científica y posteriormente del mundo entero cuando Einstein publicó su teoría en 1915. La teoría de la relatividad ha sido verificada por multitud de experimentos desde entonces y constituye uno de los avances más importantes del conocimiento humano.

Notas

(1) Para un sistema de referencia que se mueve al 60% de la velocidad de la luz el factor de Lorentz es de 1.25 por tanto la contracción relativista de la escalera será:

4/1.25 = 3.2m

(2) Para realizar la graduación de los ejes x´y t´, es decir, la distancia entre las distintas líneas espaciales y temporales dibujamos hipérbolas desde el eje S al sistema S´:

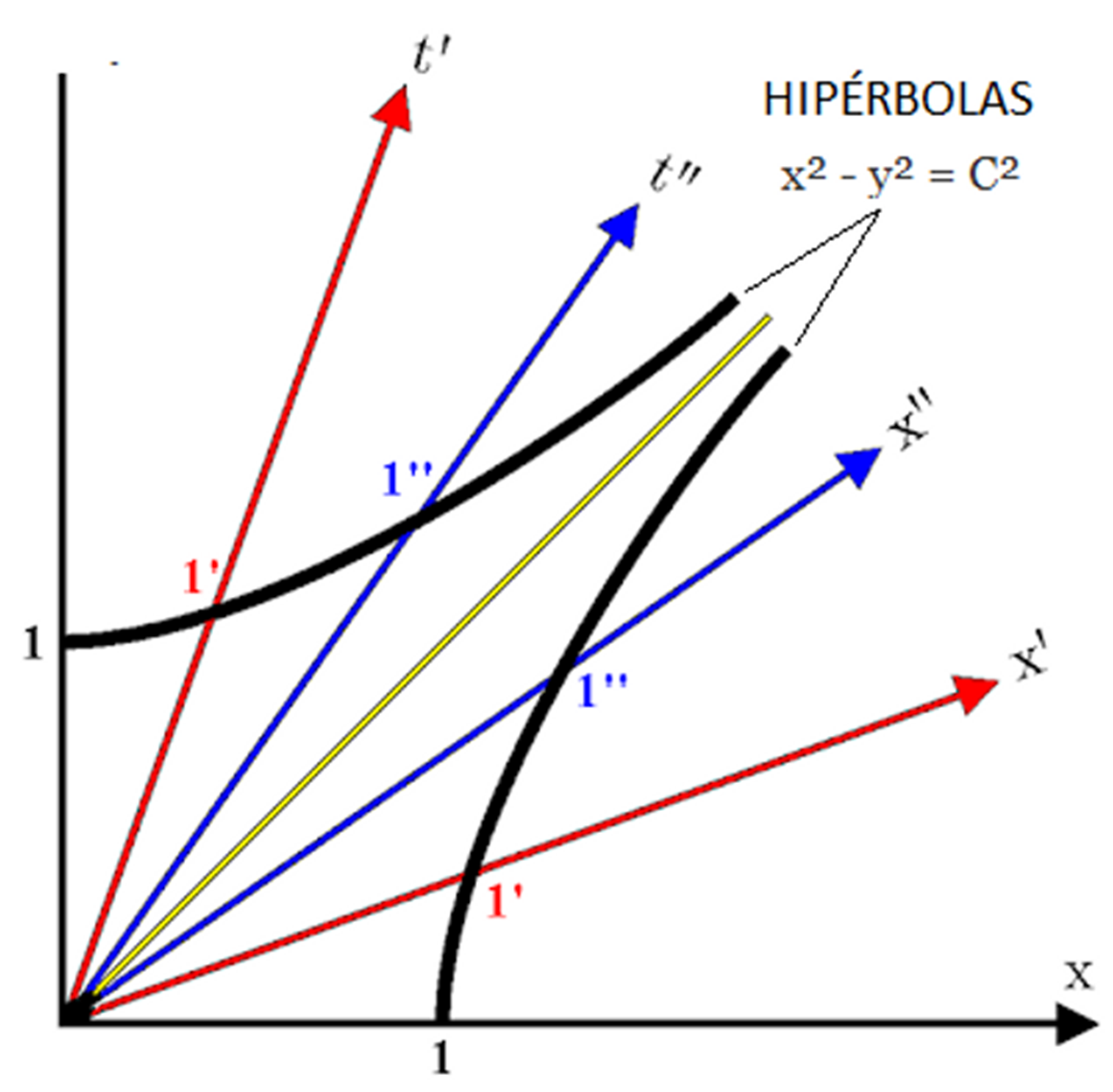
Para graduar los ejes en S´trazamos hipérbolas desde S a S´. Hay que recordar que la ecuación de la hipérbola es X²-Y²=C² que coincide exactamente con el intervalo relativista del espacio-tiempo de Minkowsky. Si nos fijamos en el diagrama la distancia desde el origen al punto 1 siempre será menor que desde el origen a 1´por tanto, la distancia de las líneas en S´será mayor que en S y por tanto los objetos en S' siempre tendrán una distancia menor como dicta el postulado de la contracción espacial relativista.