ERRORES MATEMATICOS

En la propia creatividad de las ciencias y técnicas que usan recursos matemáticos, muchos son los errores cuantitativos que se han dado y que han obligado a nuevos estudios o nuevos inventos. Ingenieros y arquitectos nos deleitan a menudo con realizaciones de gran tamaño que ponen de relieve espectaculares errores que todos podemos contemplar (excepto si el error es tan grave que la obra se hunde recién acabada). Los errores científico-técnicos afectan a los proyectos de los profesionales, pero a menudo también acaban influyendo en todos nosotros. Nuestra disponibilidad para cometer disparates en este caso es también meritoria. Lo dijo Einstein muy claramente:

"Cualquiera que no haya cometido un error es que nunca ha intentado hacer algo nuevo"

EL FALLO DEL MISIL

El 25 de febrero de 1991, durante la guerra del Golfo, un misil Patriot estadounidense no logró interceptar un misil Scud iraquí y éste mató a 28 soldados e hirió a más de 100. Lo sorprendente de este fallo es que fue estrictamente numérico, ya que el software del Patriot estaba programado para cifras binarias con 24 bits y en el cálculo del propio misil se produjo un error de tan solo 0,34 segundos, pero como la criatura iba a 1.676 metros por segundo, el desvío fue de casi medio kilómetro… y pasó lo que pasó.

LOS DÍGITOS Y LA EXPLOSIÓN DEL ARIANE 5

Cualquiera que haya usado una calculadora sabe que dispone de un límite de cifras y que si sus cálculos exceden tal limitación, la aritmética no funcionará. A los ordenadores les puede pasar lo mismo. Si al hacer un cálculo computacional con un programa que usa dígitos binarios (ceros y unos) no se hace una buena previsión de la cantidad de unos y ceros que están en juego, puede ocurrir que el programa no funcione. El problema adquiere tintes dramáticos si dicho programa es el que guía la velocidad y la trayectoria de una nave.

El cohete Ariane 5, de la Agencia Espacial Europea, el 4 de junio de 1996 explotó a los 37 segundos de haber despegado por una simple imprevisión de los dígitos con que el programa del ordenador que dirigía el vuelo debía funcionar.

¿CUÁNDO ACABARÁ LA OBRA?

Dos errores son comunes en todas las obras de arquitectura: determinar cuánto tiempo durará la obra y cuánto costará. Todos los oficios relacionados con la construcción no tienen ideas muy claras sobre la duración y la cotización de sus propias actuaciones. Siempre ocurre algo. El electricista no trajo suficiente cable, el fontanero olvidó la llave inglesa, el vidriero creyó que era mañana, etc. Y cuando se trata de una obra compleja y el arquitecto debe precisar su final, la probabilidad de que acierte es prácticamente nula. Y como el tiempo es oro, todo esto repercute en las facturas y en el coste global. Los desvíos del coste previsto también se benefician de los incrementos de precio de materiales y servicios durante el periodo de ejecución y de los replanteos y cambios realizados sobre la marcha.

Un caso colosal fue el del genial Antoni Gaudí, al cual nunca le preocupó en absoluto acabar a tiempo. Valga de ejemplo los catorce años que se tomó para acabar de diseñar el famoso banco sinuoso del Parque Güell y las enormes facturas que Güell o Milá tuvieron que afrontar. Y por supuesto en el caso del Templo de la Sagrada Familia ya el propio Gaudí decía: «Mi cliente no tiene prisa»: Dios.

GRADOS ALEMANES PARA ANGLOSAJONES

Un error cultural común es creer que los países tienden a utilizar medidas propias de científicos del lugar. Aplique en ciencia también aquello de que «nadie es profeta en su tierra». Al alemán Gabriel Daniel Fahrenheit (1686-1736) le cabe el honor de haber fabricado en 1714 los primeros termómetros fiables, a los que incorporó una escala que hoy lleva su nombre. Fabricante de instrumentos científicos y experto en física, pasó de usar alcohol a usar mercurio, y precisó el tema de la ebullición y la congelación del agua y la influencia de la presión atmosférica. En su escala, el cero (0 ºF) corresponde a lo que consideró el estado más frío posible de agua mezclada con otros elementos; 32 ºF corresponde a la congelación normal, y fijó un tope (arbitrario) de 212 ºF. Lo sorprendente es que esta escala alemana sólo tuviera éxito entre los anglosajones.

CELSIUS: UN SUECO BAJO CERO

El sueco Anders Celsius (1701-1744) fue profesor, matemático, físico y astrónomo, montó el primer observatorio astronómico en Suecia y formó parte de la expedición científica que verificó el achatamiento del planeta en los polos. Pero su fama se debe a su escala de temperaturas. Celsius consideró «cero grados» la temperatura en que el agua se hiela y «cien grados» la correspondiente a la ebullición del agua. Así, los grados Celsius corresponden a la división en cien partes de la escala de 0 ºC a 100 ºC. Lo que sorprende es que, tratándose de un sueco —país de temperaturas muy extremas—, Celsius tomara una escala que le obligó a dar la temperatura de su lugar usando grados negativos

¿CELSIUS O FAHRENHEIT?

Un problema para viajantes es asumir que en el mundo de los termómetros hay dos escalas diferentes para medir las temperaturas: la escala Celsius (ºC) y la escala Fahrenheit (ºF). Si una va de 0 a 100 ºC, la otra va de 0 a 212 ºF, pero en ambos casos el cero corresponde a situaciones distintas, con 0 ºC = 32 ºF. Para poder pasar de C (Celsius) a F (Fahenheit), hay que usar

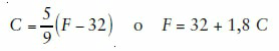
Es frecuente que los pilotos de aviación informen de las temperaturas en el aeropuerto de llegada en Celsius o en Fahrenheit según su tradición cultural. Algunos comandantes dicen los grados sin especificar el sistema (¡horror!). Y muchos viajeros confunden la información («¡Qué bien estaremos a 20 grados!»). Para los adictos al Celsius que reciben atónitos informaciones en grados Fahrenheit, una solución de emergencia mental es hacer la aproximación 5/9 ˜1/2 y efectuar el cálculo (F - 32)/2, lo cual dará una idea de por dónde va el asunto. Así, 20 ºF son unos –6 ºC, 30 ºF son –1 ºC, 40 ºF son 4 ºC… o para que la habitación esté a unos 20 ºC, el termostato ha de marcar 68 ºF.

LOS KELVIN NO SON GRADOS

El matemático y físico William Thomson, lord Kelvin (18291907), cuya genialidad ya se manifestó cuando a los 10 años acudió a la Universidad de Glasgow, nos legó interesantes aportaciones científicas. Una de ellas fue una escala absoluta de temperaturas que fijaba el 0 absoluto que termodinámicamente puede darse, equivalente a –273,15 ºC en la escala Celsius o a –460 ºF en la Fahrenheit. La unidad de esta escala absoluta de Thomson se denominó «kelvin» (K), y por tanto K = ºC + 273,15. Pero como es una escala de temperaturas y ha de convivir con la Celsius y la Fahrenheit, a menudo se comete el error de hablar de «grados Kelvin» o incluso de escribir 373 ºK. Debe ser 273,15 K = 0 ºC y no 273,15 ºK = 0 ºC.

MÁS CERCA DEL SOL, MÁS CALIENTES

Uno de los errores más colosales (pero más extendidos) es la falsa creencia de que las estaciones del año tienen que ver con la cercanía de la Tierra al Sol. Las cuatro estaciones quedan determinadas por las inclinaciones de la Tierra en su constante giro elíptico alrededor del Sol, y los dos solsticios (invierno y verano) y los dos equinoccios (primavera, otoño) marcan los inicios estacionales. Es precisamente este carácter inclinado del planeta el que implica que el hemisferio Norte (o Boreal) y el hemisferio Sur (o Austral) tengan intercambiadas las estaciones del año. En un mundo global esto tiene enormes consecuencias: los australianos vienen a España en enero y usted puede ir a esquiar a la Patagonia en agosto.

METEOROLOGÍA VERSUS CLIMATOLOGÍA

Las publicaciones del tiempo atmosférico a corto plazo de los meteorólogos y las que se hacen en climatología a largo plazo son hoy el resultado de una inmensa combinación de informaciones (medidas e imágenes) que los satélites mandan, y sofisticados modelos matemáticos extrapolan (a partir de los datos) la posible evolución del tiempo. Las predicciones locales «para hoy» no resultan muy arriesgadas, las de la semana próxima tienen una credibilidad moderada (incluyendo a menudo referencias a las probabilidades de lluvia, viento, etc.) y a largo plazo… no es preciso ni que se lo lea. Los errores en el largo plazo meteorológico pueden ser monumentales, pues los actuales modelos para hacer predicciones tan complejas no dan más de sí.

EL LÍO DE LOS CLIMAS

En las informaciones climatológicas encontrará una rica nomenclatura que puede orientar en términos generales lo que es común en una zona: climas secos (áridos, semiáridos), climas fríos (continental húmedo o suave), clima polar (tundra, polos), clima templado lluvioso (oceánico, chino, mediterráneo), y por supuesto el ecuatorial, el tropical, el monzónico, etc. Quien no tiene un clima es porque no quiere. Pero no debe cometerse el error de creer que con una palabra mágica («tienen clima oceánico») ya pueden sacarse conclusiones para programar un viaje.

¿VERANO TÓRRIDO EN MÉXICO?

No siempre el sentido intuitivo lleva a conclusiones acertadas. En temas de temperaturas, por ejemplo, nos dejamos llevar frecuentemente por «tópicos» y por el error de creer que «en todo el mundo» las épocas de lluvia, calor, etc., son las mismas. Por ejemplo, ¿cuándo llueve más en México D.F. o cuándo hay más polución? Pues entre mayo y octubre es la época lluviosa, y por tanto la máxima polución se da en invierno… y los meses más calurosos son abril y mayo.

¿1998 O 1934?

En pleno debate sobre el cambio climático y sus evidentes implicaciones, ocurrió lo peor. La NASA tuvo que reconocer que algunos de sus informes sobre la evolución de las temperaturas no habían sido correctos. Que 1998 no fue el año más caliente en Estados Unidos sino 1934 (con datos desde 1880), y los datos de 2006 sobre calentamiento fueron de hecho superados en 1921…Así pues, aparecieron datos más alarmantes en la década 1930-1940 que en la actualidad.

Tantos han sido los números acumulados sobre el cambio climático que el problema ha quedado bien retratado. No obstante, entre todos los datos usados por el Panel Intergubernamental de Cambio Climático de la ONU, algunos revisados en 2010 resultaron ser fraudulentos: errores de cálculo del deshielo del Himalaya, un estudio basado en «opiniones» de escaladores y guías de montaña, disparates sobre el bosque amazónico, etc.

PROSPECTIVA CLIMÁTICA

Los numerosos estudios del cambio climático buscan a menudo justificaciones numéricas que pueden ser discutibles, sin que ello invalide las evidencias de un cambio global. Por ejemplo, en Estados Unidos se ha afirmado que «desde la mitad de los setenta la temperatura media sobre la superficie terrestre se ha calentado cerca de 1 ºF», y se calcula que ahora «el calentamiento es de 0,32 ºF por década, o sea, 3,2 ºF por siglo». ¡Una precisión extrema! También las extrapolaciones son diversas, y hoy disponemos de análisis de evoluciones de las temperaturas de «…los últimos 425.000 años».

ERRORES QUE SON ACIERTOS

A veces cometer un error puede llevar a un gran acontecimiento. Y éste fue el caso de Cristóbal Colón. Que el famoso navegante tenía información «privilegiada» sobre la existencia de tierra a unas 750 «leguas» de las islas Canarias y que con ello convenció a los Reyes Católicos para que financiaran su viaje, resulta hoy más que evidente. El gran error de Colón fue creer que su aventura terminaba en Asia («a 135 grados de circunferencia») y acabó descubriendo América (a 229 grados). Además, diversos errores durante la navegación (incluyendo la distancia a navegar) permitieron que acabara desembarcando en La Española. Hoy sabemos cómo es el mundo físico y, evidentemente, en cualquier dirección hacia el oeste hubiese descubierto América.

Curiosamente, la figura de Colón se ha usado a veces para decir que «los matemáticos son como Cristóbal Colón, porque no saben a dónde van, si llegan a algo tampoco saben qué es, y buscan dinero público para financiarse».

¿EL SEÑOR LITRO?

Justificar la conveniencia de usar la letra L mayúscula para designar la popular unidad de volumen no parece un tema difícil, pues en el Sistema Internacional de Unidades se admite tanto L como l. Pero como en general se recomienda que las mayúsculas se reserven para las unidades que lleven un nombre propio, en 1977 el profesor K. Woolner de Canadá se inventó una leyenda sobre la existencia de un señor llamado litro.

El referente era Claude Émile Jean-Baptiste Litre, un francés nacido el 12 de febrero de 1716, prestigioso fabricante de botellas de cristal para vino, introductor de diversas medidas en relación con el vino y sus botellas, que mantuvo correspondencia con Celsius y escribió un tratado sobre estudios volumétricos, el cual influyó años después en la comisión dirigida por el matemático Lagrange que estudió la creación del sistema métrico decimal. El nombre de la nueva medida se adoptó en recuerdo de Litre. Lo curioso, e internet ha contribuido a ello, es que estas historias inventadas, casi infantiles, se difunden luego como si fuesen ciertas.

EL APARATO «ES» LA MEDIDA

Las tradicionales medidas de longitud inducen al error frecuente de creer que para «medir» debe haber «algo tangible» y con el uso de patrones para proceder a cuantificar. Sin embargo, para superficies y volúmenes se impone un cálculo a partir de medidas lineales y no el uso de aparatos. ¿Y el tiempo? Es el reloj el que «determina» el propio objeto que se va a medir. A menudo las medidas indirectas ligadas a aparatos (piense en los termómetros) acaban siendo referentes más próximos que la propia realidad que se va a medir.

MEDIDAS DE SILLAS Y MESAS

Es un disparate creer que las medidas de mesas y sillas para comer no tienen especial importancia. Aquí nos vamos a referir a lo que los técnicos consideran medidas óptimas para comer en una mesa como Dios manda. De entrada, la mesa debe tener una superficie perfectamente plana y es recomendable que tenga una altura de 75 centímetros. Las sillas deben tener un asiento situado a una altura de 45 centímetros, con una amplitud de 45 cm y 50 cm de profundidad cuyo respaldo llegará al menos hasta los 80 cm de altura. Enfrente de cada comensal debe presuponerse un rectángulo para poder comer con dignidad (tomar cubiertos, poner vasos y copas, tener platos, etc.) de unos 65 cm de ancho por 35 cm de profundidad.

El siguiente factor a tener en cuenta son las distancias alrededor de cada comensal. Entre el borde de la mesa y la pared deben quedar al menos entre 65 y 70 cm para que la persona pueda acceder a la mesa o levantarse y salir. Pero deben preverse unos 95 cm si puede haber tránsito de personas por detrás o hasta 120 cm si hay servicio por detrás del comensal. Por supuesto, por debajo de la mesa se supone que la rodilla del sentado puede llegar hasta 35 cm por debajo de la mesa y en el suelo los pies pueden llega hasta los 40-45 cm, desde la proyección del borde. Las medidas son, pues, un factor importante de comodidad y de funcionalidad en el momento de sentarse a la mesa.

UN ERROR MÍNIMO

Los ingenieros franceses Jean Delhambre y Pierre Méchain fueron responsables de las mediciones topográficas del trozo de meridiano terrestre de París entre Dunquerque y Barcelona, para así poder hacer el patrón físico del metro como «diezmillonésima parte del cuadrante de meridiano terrestre». Es decir, por definición, cualquier meridiano terrestre debía medir 40.000.000 de metros, pero el problema era determinar esta unidad. Delambre y Mechain sólo cometieron un error del 0,023 %, lo cual para 1799 fue todo un récord.

LA DISTANCIA DE LA MARATÓN

Muchas son (y muy concurridas) las maratones populares: Nueva York, Boston, Chicago, Berlín, París, Estocolmo, Madrid, Barcelona… pues la afición por las carreras atléticas ha ido en aumento durante el siglo XXI, tomando siempre como referencia, desde 1896, las maratones olímpicas. El lío viene cuando se trata de perfilar la distancia que debería recorrer una maratón.

Si atendemos a diversas leyendas griegas sobre héroes atléticos que llevan noticias desde el lugar físico llamado Maratón a Atenas (menos de 40 km), se entiende que en 1896 se fijaran 40 km como una buena distancia a recorrer. Pero en las olimpíadas actuales se recorre, desde 1908, la peculiar distancia de 42,195 km, con tres decimales. El motivo es muy banal: el príncipe de Gales pidió al barón de Coubertin que en los juegos ingleses de 1908 la maratón fuese del Castillo de Windsor (su casa) hasta el estadio olímpico White City de Londres… añadiendo unos metros dentro del estadio para que la meta estuviese frente al palco presidencial. La necesidad de los 3 decimales en el 42,195 km ya hace sospechar que detrás de esta distancia se esconde toda una historia.

UN VUELO DE MONTREAL DE 1984

Un auténtico hito en la historia de los errores aeronáuticos (pero con final feliz) ocurrió el 23 de julio de 1984. Un vuelo de Air Canada en Boeing 767 paró en Montreal para repostar combustible con vistas a llegar a su lejano destino en Edmonton. Advirtiendo que los indicadores del contenido de combustible de los tanques del avión no funcionaban, los del servicio de mantenimiento de Montreal pudieron medir que en el depósito había 7.682 litros y que se precisaban 22.300 kilogramos para completarlo. Pero la tripulación calculó (¡erróneamente!) que sólo necesitaban 4.916 litros adicionales, y éstos fueron los que el camión cisterna de Montreal inyectó. El error fue considerar que como un litro correspondía a 1,77 libras, al multiplicar (7.682 + 4.916) × 1,77 obtuvieron 22.298 libras o sea 10.115kilogramos de fuel… la mitad de lo necesario. Es decir, 1,77 no era el número de kilogramos por litro y el factor fue usado incorrectamente.

La habilidad de la tripulación al quedarse sin combustible y la suerte de poder aterrizar en una base canadiense confirió un final feliz a un error que hubiese podido ser fatal. 

MARTE, MILLAS Y KILÓMETROS

El 23 de septiembre de 1999, la NASA perdió contacto para siempre con la nave Mars Climate Orbiter justo cuando este artefacto de 125 millones de dólares estaba a punto de culminar su llegada al planeta Marte después de un largo viaje que se había iniciado el 11 de diciembre del año anterior. ¿Cuál fue el problema por el que este millonario proyecto fracasó? ¡Un error en el sistema de medidas utilizado! La NASA trabaja siempre con el sistema métrico decimal, pero una de las empresas que colaboraron en el proyecto trabajó con unidades del sistema anglosajón. Y claro: una cosa es aproximarse a 60 km (37 millas) y otra a 150 km (93 millas). Posiblemente éste sea el error multiplicativo más caro de la historia. 

MEDIDAS ESCONDIDAS 

Desde el Antiguo Egipto, las extensiones de tierras tuvieron implicaciones fiscales y por tanto no es de extrañar la tradición milenaria de camuflar las medidas reales para pagar menos impuestos. A pesar de que los satélites y los teodolitos van a favor de la hacienda pública, no son raros los juicios sobre extensiones de terrenos. ¿Cuántos terrenos de La Coruña se declararon como «un ferrado de extensión» cuando medían mucho más? Pero no sólo el fisco incita al escondite. La coquetería humana también se ocupa de esconder años, kilos, etc. 

EL MUSEO VASA  

Que un error de cálculo provoque el hundimiento de un barco es algo que ha ocurrido a lo largo de la historia. Pero que el barco hundido se reflote y se construya un edificio-museo sólo para exhibir a la criatura ya es menos usual. El Museo Vasa de Estocolmo contiene los restos del hermoso barco que en 1628 se hundió a tan sólo 1.500 m del lugar en que fue botado al agua. ¿Motivo? No se calculó bien que el barco-orgullo nacional pudiera resistir el enorme peso de los cañones que se le colocaron.  

EL LÍO DE LOS GRADOS ALCOHÓLICOS 

La palabra grado se asocia normalmente con temperaturas. Pero en el mundo de los sabores convive con el (interesante) grado alcohólico. ¿Qué significa que un vino tenga 13 grados o que un ron tenga 40? El alcohol de licores, vinos, cervezas, etc., surge de procesos de destilación de líquidos alcohólicos procedentes de la fermentación de azúcares de zumos de frutas o hidratos de carbono. Es costumbre europea que los grados alcohólicos correspondan al porcentaje de volumen de alcohol presente en la mezcla (% vol. o %VV); no es, pues, una medida, sino un tanto por ciento camuflado del cual debe notar que es en volumen y no en masa. Esto fue acordado por la Organización Internacional de Metrología Legal. Así, en un ron de 40 grados el volumen de alcohol presente en la botella es del 40 % pero en masa representa solo un 35 %. Como la densidad del alcohol es menor que la del agua, los porcentajes de masa de alcohol resultan ser inferiores a los de volumen.

Pero en las bebidas norteamericanas podrá observar la referencia a los grados proof, que son la mitad de los grados europeos. Al menos es fácil pasar de unos grados a otros. Pero también ha existido o aún existe toda una gama de otros grados relacionados con contenidos de alcohol: el grado Richter, por ejemplo, que hace referencia al tanto por ciento en masa. 

QUEIMADAS, CREMATS Y LEYENDAS 

La presencia del fuego en las queimadas y cremats ha inducido a numerosas consideraciones sobre si el alcohol desaparece, a qué temperaturas se produce la degradación alcohólica, etc. Lo ha explicado magistralmente Claudi Mans: es un error creer que primero se evapora el alcohol y después el agua. Si un ron o aguardiente de «40 grados» se pone a calentar en un recipiente (por ejemplo, con agua y café), si el agua hierve a 100 ºC y el alcohol etílico a los 78,3 ºC, a medida que la temperatura aumenta se van desprendiendo vapores de ambos componentes y hacia los 83 ºC empieza la ebullición, disminuyendo en el proceso la proporción de alcohol. 

DISPARATES ÁCIDOS 

Un popular parámetro químico (con valores entre 0 y 14) para medir la acidez o alcalinidad es el llamado pH. El caso neutro (agua) tiene pH 7, lo ácido por debajo de 7 (vinagre: pH 3; leche: pH 6…) y lo alcalino por encima del 7 (agua de mar: pH 8; bicarbonato disuelto: pH8…). Parece sencillo, ¿no? Pues va a ser que no. El primer disparate es confundir el pH con los grados de acidez en los aceites (un aceite de 0,4 grados sería como ingerir sulfúrico). El segundo disparate surge, por ejemplo, al comparar un pH 5 con un pH 6: ¡el pH 5 es 10 veces más ácido que el pH 6! La definición oficial de este pH (donde aparecen logaritmos y potencias de 10) lleva a esto; detrás de las unidades del pH están las potencias de 10. 

ALTURAS DE LOS LUGARES

El concepto de altura de un lugar («El monasterio se encuentra a 400 m de altura», «Nevará por encima de los 1.200 m»…) es algo relativo al «nivel 0 del mar», y éste se fija en cada país. Por tanto, esta altura no es un concepto universal en la Tierra. En España, por ejemplo, se toma como referencia del nivel 0 el de Alicante, en Francia el nivel 0 es el de Marsella, en Austria se refieren al nivel del mar Adriático en Trieste, etc. Uno de los últimos puentes sobre el Rin que se construyó simultáneamente desde Suiza y Alemania tuvo el problema de que una parte no enlazaba con la otra (54 cm de diferencia). ¿Cuál había sido el error? ¡Países diferentes tienen niveles 0 distintos!

Más curioso resulta que en la delimitación de terrenos para construir se tomen mal las medidas de referencia de las fincas colindantes y se levante un edificio en el terreno equivocado. No es un fenómeno extraño. Ya puede imaginarse la cara de horror del arquitecto que llega al lugar donde la estructura ya alcanza cuatro pisos y grita: «Paren, paren, que nos hemos equivocado de solar». 

ERRORES SISTEMÁTICOS

 La aparición de errores accidentales o fortuitos cuando se realizan medidas es plenamente comprensible, y como ocurre poco, la cosa no es grave. Lo que resulta ya más lamentable son los errores sistemáticos, los que se repiten muchas veces. Si éstos ya se saben por adelantado («Este reloj adelanta 2 minutos cada día»), la cosa es fácilmente soportable. Si son resultado de incompetencias del medidor que metódicamente repite su error, la cosa es lamentable. 

VENTANAS, COLUMNAS, ESCALERAS 

Elementos arquitectónicos estupendos y bien calibrados pueden resultar esperpénticos cuando no se cuida el proyecto global y no se consideran las relaciones entre dichos espacios: el error de colocar las columnas o pilares junto a las ventanas —lo que impide su uso—, olvidos de puertas, escaleras mecánicas que acabarían con nuestras cabezas empotradas en el techo superior, etc. El error de no mirar los proyectos globalmente puede suponer que al juntar los diferentes elementos resulte un desastre de diseño.

Una moda actual en las ciudades es colocar en la aceras objetos fijos (esferas, cilindros metálicos…) para disuadir a los conductores de aparcar allí. Esto parece correcto, pero en muchos casos la aplicación sistemática de este principio lleva a situaciones ridículas en las cuales ni aparcan coches ni pueden pasear los peatones. 

NORMATIVAS Y CÁLCULOS 

En enero de 2009, rachas de viento inusuales azotaron Cataluña y provocaron pérdidas humanas y materiales. Las normativas antiguas no exigían prever grandes vientos y su efecto «succión». Por eso volaron tantos techos metálicos. O se cambian las normativas, se recalculan las construcciones y se hacen reparaciones previsoras, o sólo queda rezar para que no ocurra nada. Las normativas no pueden ser eternas. Su cumplimiento legal no es garantía de que en el futuro no pueda ser recomendable cambiar los requerimientos técnicos. El gran problema es que lo hecho sigue en pie. No es preciso que abandone precipitadamente su casa y vaya a dormir a la calle, pero si algún día en una reunión de vecinos se plantea revisar algo de acuerdo con las normativas actualizadas, preste un poco de atención. 

HORMIGÓN ARMADO 

Un error de cálculo muy extendido es creer que hay materiales que duran «eternamente» como, por ejemplo, el hormigón armado. Este popular material da a los usuarios sensación de seguridad. «Está hecho en hormigón armado, durará para siempre», exclaman con orgullo personas que no entienden el hormigón, pero confían en el «armado». Las nuevas normativas vigentes son hoy mucho más rigurosas con los cálculos del hormigón armado que las de antes, que preveían una duración garantizada de sólo unos 50 años. El talón de Aquiles de esta forma de construir es la oxidación del hierro interior. El error es no hacer lo necesario para evitarlo. 

¿CUÁNTOS ANCHOS DE VÍA HAY? 

La mayoría de los españoles responde a esta pregunta con un rotundo dos. ¡Error! La situación es mucho peor: ¡hay seis! En efecto, el más común es el ancho ibérico de 6 pies de Burgos, equivalente a 1,668 m, medida superior a la europea por usar un múltiplo exacto del pie castellano, pues se creía que dicha medida podía dar más estabilidad a los trenes que circulaban por la accidentada orografía del país. Creyeron que se requerían máquinas más potentes con mayores calderas, pues se suponía que la magnitud de la caldera influía en la presión del vapor sobre los pistones. Recientemente leí una nota de un veterano ingeniero de caminos que defendía el ancho de vía español y reclamaba que el AVE se hiciera con él. Junto al ancho ibérico coexiste el internacional (1,435 m) de las líneas AVE, más algunos metros y ferrocarriles catalanes. Pero también hay el ancho de Palma-Sóller, de 0,914 m; el del metro madrileño, de 1,445 m; el ibérico antiguo, de 1,674 m en la línea I del metro barcelonés, y el ancho métrico o FEVE de 1 m en ferrocarriles de Barcelona, Valencia y País Vasco.

RAMPAS IMPOSIBLES 

Rampas casi imposibles en accesos a garajes privados (¡y algunos en garajes municipales!) son muy habituales. Se supone que la potencia del automóvil y la habilidad del tigre que va al volante ya salvarán la caída libre y el ascenso vertical. Lo que ya es más lamentable, en bajadas de aceras y accesos a edificios, son muchas rampas para personas, muy difíciles de usar con sillas de ruedas, carritos de la compra, cochecitos infantiles, etc. La pendiente asequible debe imponerse al diseño de la rampa, y es un gran error no pensar bien el ángulo de inclinación razonable y las posibles repercusiones de un ángulo demasiado grande. 

¡SUERTE QUE LA TORRE DE PISA ESTÁ INCLINADA! 

A veces un error puede tener tanta gracia que sea aconsejable mantenerlo eternamente. La inclinación de la torre de Pisa es un caso emblemático de error geológico-constructivo, donde la condición del subsuelo cedió sin piedad al enorme peso de la torre… y gracias a ello la ciudad de Pisa ha encontrado su modus vivendi: los millones de turistas que acuden a Pisa —y gastan dinero allí—, para poder ver y retratarse erguidos frente al inclinado monumento. En la última gran restauración, de gran complejidad y brillante resolución, logró frenarse la inclinación y por tanto, asegurar una larga vida a la estructura inclinada. 

LA PREDICCIÓN TÉCNICA DE BILL GATES 

Para suerte (y fortuna) de Bill Gates, su alocada predicción de 1981 no ha sido cierta:

"640 Kb —de memoria— deben ser suficientes para cualquiera"

Pero con la probada inteligencia de Gates, igual esta frase era una malévola información para sus competidores. 

MEDIDITIS 

En una ocasión la famosa Jeanne Parain-Vial, estudiosa del llamado estructuralismo filosófico, afirmó: 

"El aparato matemático da a conclusiones discutibles, a veces erróneas, una apariencia peligrosa de resultado científico"

En efecto, es un error monumental creer a ciegas que la presencia de datos matemáticos ya asegura la bondad o la certeza de algo. Esto lo saben muy bien los que viven precisamente de engañar con números en astrología, adivinación, tarot, ovnis, etc. Aunque sesudos cálculos astronómicos sobre la situación de los planetas permitan hacer su «carta astral», no confíe en que los resultados predictivos sobre sus nuevos amores y su ingreso inmediato al club de los millonarios se hagan realidad. 

EL PESO DE LA CULTURA 

He aquí un hecho verídico que se dio en una facultad universitaria de Valencia. Dado que la biblioteca del centro estaba situada en la planta baja, a las autoridades académicas del lugar se les ocurrió que sería mucho mejor situarla en el último piso del edificio, pues era evidente que los interesados en ir allí no dejarían de hacerlo por estar los libros situados arriba. Y el traslado empezó. Todo parecía ir bien, salvo que pronto tuvo que paralizarse para proceder a un refuerzo estructural contundente de todo el edificio. Trasladar una biblioteca con miles de libros no es lo mismo que trasladar unas aulas o una sala de estudios: el enorme peso de los libros ponía a prueba una planta superior que no fue diseñada para aguantar tanto peso.

A nivel casero, poca gente aplica el principio recomendado de procurar colocar cualquier librería llena de libros en una posición perpendicular a las vigas del suelo que debe sostener a la mole. Los arquitectos calculan con muy generosos márgenes los suelos para que éstos puedan soportar, con dignidad estructural, cargas muy diversas, pero no puede pretenderse que grandes pesos como las bibliotecas puedan ubicarse en cualquier lugar. 

EL TERREMOTO DE LA PLATAFORMA 

Ocurrió el 23 de agosto de 1991 en el mar de Norte, en Noruega. El hundimiento de parte de la plataforma petrolífera Sleipner A provocó un pequeño terremoto local y una pérdida económica de unos 700 millones de dólares. El motivo de tan dramático comportamiento de la plataforma fue un típico error de cálculo al usar el programa informático NASTRAN para diseñar estructuras por el llamado método de los elementos finitos: hubo una desviación de un 47 % en la aplicación del modelo teórico a la pesada plataforma que debía apoyarse en unos macropilares que llegaban a una profundidad de 82 metros. 

EL PUENTE DE TACOMA 

El colapso vibratorio del puente de Tacoma Narrows, en la ciudad estadounidense de Seattle, tan sólo cuatro meses después de su inauguración, fue consecuencia de errores del cálculo al haberse usado un modelo en el que no se tuvo en cuenta el posible efecto de los vientos de la zona. Las oscilaciones longitudinales sí se habían calculado bien, pero los efectos de los vientos cruzados sobre la estructura no se tuvieron en cuenta, es decir, no se supo prever que la resistencia al aire que tenía la estructura causaba contundentes turbulencias que acababan haciendo oscilar el puente. El 7 de noviembre de 1940, y a pesar de que los vientos eran de sólo 64 kilómetros por hora, este hermoso puente de 1.600 metros de longitud se derrumbó tras unas muy violentas convulsiones.

La suerte quiso que justo antes de la catástrofe sólo hubiese un coche que cruzaba el puente, que el conductor pudiese salir corriendo y que, al tratarse de un profesional de la imagen con cámara en ristre, Leonard Coastworth pudiera dejarnos a todos la película del fatal desenlace (hoy colgada en internet). Esta película es un clásico que todos los estudiantes de ingeniería del mundo ven cada año a fin de que los errores del pasado no se repitan. La única víctima de la catástrofe fue el pobre perro de Leonard, que no pudo seguir a su dueño y murió dentro del coche abandonado.

Este error con desastre final, que pilló desprevenidos a ingenieros y autoridades, no sorprendió en absoluto a los usuarios habituales del puente, pues durante los cuatro meses que pudieron transitarlo lo bautizaron con el sobrenombre de la Gertrudis Galopante, pues los temblores y oscilaciones de la estructura del puente al pasar los vehículos ya casi se habían convertido en una atracción turística. El ingeniero Theodore Von Kármán había advertido del tema, pero no fue refrendado por sus colegas.

Años después de Tacoma, un puente del estado norteamericano de Minnesota también se vino abajo por errores de diseño y cálculo estructural, causando diversas muertes y muchos heridos. Este caso fue citado por Barack Obama durante su campaña, e insistió en la necesidad de dedicar fondos para revisar estructuras deficientes, a cuyo cometido se han destinado muchos dólares desde 2009. 

LA GEOMETRÍA DE UN CROISSANT 

Se atribuye a Antonin Carême (1783-1833), conocido como el cocinero de los reyes y el rey de los cocineros, la curiosa afirmación: 

"Las bellas artes son cinco en número, concretamente: pintura, escultura, poesía, música y arquitectura, siendo la principal rama de esta última la pastelería" 

¿Cómo ven los arquitectos a los productos pasteleros? El arquitecto Enric Miralles publicó hace años (con Eva Prats) en el número 49-50 de la revista El Croquis, un demoledor escrito titulado «Cómo acotar un croissant». Con una aplicación extraordinariamente rigurosa de las técnicas de expresión gráfica se presentan junto a la imagen de un simple croissant todo tipo de secciones y datos de acotación, medidas y ángulos. El texto está redactado como un guión académico para llevar a cabo esta «importante representación». Citaré sólo la entrada: 

«A. Definición: Una superficie se envuelve sobre sí misma, y aparece un interior que se forma al sobreponerse al exterior. Luego los extremos se cierran sobre sí mismos y forman la envoltura sobre la que se agrupan los pliegues. Reconoceremos esta forma en el interior de la bóveda bucal […] Al medirlo, las cotas devuelven la transparencia a esta forma, con todas sus cualidades negativas: incolora, inodora y sin sabor. Y un croissant, la media luna en Argentina, es para ser comido…»

Nunca un croissant pudo soñar ser el protagonista de una tan espectacular crítica al academicismo universitario: geometría crítica.

LOS ÁNGULOS DE BOFILL 

El popular arquitecto Ricardo Bofill tuvo la mala suerte de que en un programa de televisión en directo se produjera una llamada de un espectador cuya única pregunta fue: «¿Sabe el señor Bofill cuáles son los ángulos en una escuadra y en un cartabón?» El famoso arquitecto no supo dar respuesta. 

DISPARATES DE MATEMÁTICOS 

PI SEGÚN OFICIOS 

Populares son las consideraciones numéricas según diferentes oficios. Del popular pi se dice que para un matemático es la razón entre perímetro de una circunferencia y diámetro. Para un ingeniero es casi 22/7. Para un físico es 3,14159 más o menos 0,000005. Para un programador informático es 3,141592653589 con doble precisión. ¡Por sus precisiones los conoceréis! 

Hay dos tipos de matemáticos: los que se equivocan al contar y los que no se equivocan. En algunos casos, los errores provienen de las limitaciones de la época y, por tanto, podemos denominarlos benévolamente como «aproximaciones» (pi igual a tres…). Pero en otros casos pueden ser resultado de operaciones equivocadas, razonamientos falsos, demostraciones incompletas, etc. En esta segunda categoría cabe confiar en que a la larga el caso se subsane y el tema se resuelva bien. Lo curioso es que a veces, en cuestiones de números aparentemente simples, las esperas de la verdad pueden prolongarse, como veremos, siglos o incluso milenios. Suerte que la paciencia es también una virtud matemática.

TANTOS POR CIENTO Y MATEMÁTICAS 

Una popular definición de matemáticas dice: 

"La matemática está hecha de un 50 % de fórmulas, un 50 % de demostraciones y un 50 % de imaginación"

Un 150 % que no cuadra: ¿sobra algo?  

NO SIEMPRE LA BIBLIA TIENE RAZÓN 

En el Antiguo Testamento (I Libro de los Reyes 7:28 y Crón. 4:2) se informa: 

"Hizo asimismo un mar de fundición, de diez codos del uno al otro lado, redondo, y de cinco codos de alto, y ceñíalo en derredor un cordón de treinta codos"

 Si la circunferencia era de 30 codos y el diámetro era de 10, resulta el valor bíblico de pi igual a 30/10 = 3… una aproximación peor que las conocidas antes de que este Antiguo Testamento se escribiera. Aquí no hay una cuestión de fe, sino un tema de números. 

UN NÚMERO PI FALSO  

En los supermercados brilla con luz propia una magnífica salsa de pimientos del piquillo a la que han bautizado «2p». No queda claro si usan dos pimientos o quieren remarcar la doble sílaba pi en pimiento y piquillo. Un uso inaudito de p no como número, sino como abreviatura. Y fatal para la exportación, pues no en todos los idiomas los pimientos empiezan por pi. El bote de esta salsa en Nueva York aún será más surrealista. 

ARISTÓTELES COMO DENTISTA 

El gran filósofo griego Aristóteles (384-322 a. C.) fue un hombre casado (dos veces), aunque debía ser muy tímido, pues siempre defendió que «las mujeres tenían menos dientes que los hombres». Como ya comentó Bertrand Russell (1872-1970), «nunca se atrevió a examinar las bocas de sus dos esposas». Cuando esta falsedad dental se podía eliminar contando, es sorprendente que un filósofo renunciara a ello.

Tampoco tenía Aristóteles muy claras las ideas sobre contar cosas en general. Sirva de muestra su celebrada proclama «El todo es más que la suma de sus partes», que si bien en su Metafísica puede tener un sentido, como ayuda a la aritmética es fatal.

MALOS TIEMPOS PARA PI (1719-1945) 

El reto de calcular muchos decimales del número pi ha acompañado a la historia matemática desde sus inicios. En 1719, De Lagny calculó 127 decimales de los cuales 112 eran correctos, y en 1794 Von Vega llegó a los 140, de los que sólo 136 eran correctos. Los primeros 200 decimales los logró Joham Martin Zacharias Dave (1829-1861) en 1844, aclarando que en los 208 decimales que había dado William Rutherford en 1824 había un error a partir del decimal 153.

En 1847, Thomas Claucren (1801-1885) dio 248 decimales, y para salvar su honor Rutherford calculó en 1853 los 440 primeros decimales. Pero dos años después Richter calculó 500. El gran avance siguiente lo hizo William Shanks en 1873-1874 al publicar los primeros 707 decimales, conocimiento que no fue desmentido hasta que en 1945 Ferguson pudo determinar que desde 1874 se había mantenido un error de Shanks a partir del lugar 527. En 1946 Ferguson dio los primeros 620 decimales correctos usando una calculadora de despacho y halló 710 en enero de 1947, y 1.808 en septiembre del mismo año. Y a partir de aquí entraron en acción las computadoras. Este cálculo manual del número pi demuestra que la paciencia humana es infatigable. 

MENTES PRODIGIOSAS 

Ésta es la triste historia de dos calculistas mentales: Maurice Dagbert y Alexander Craig Aitken. Estas dos prodigiosas mentes lograron memorizar los primeros 707 decimales de pi… tal como los había calculado Shanks. ¡Qué mala suerte! Aitken conoció más tarde los nuevos dígitos correctos de pi y tuvo la habilidad de memorizar de nuevo los decimales.

UN MATEMÁTICO INGENUO 

Michel Chasles (1793-1880) fue un hombre acreditado y reconocido por sus escritos sobre geometría, pero un día su ingenuidad le hizo perder parte de su buena reputación. Chasles pagó 140.000 francos (una fortuna entonces) por 27.000 documentos manuscritos que el falsificador Vrain-Denis Lucas había estado inventando. La enorme cantidad de 27.000 escritos ya debería hacer dudar de su autenticidad. Con gran orgullo, Chasles presentó a la Academia de Ciencias la prueba epistolar de que la teoría de la gravedad era un descubrimiento francés, comunicado por Pascal a Newton. Pero tras comprobar la caligrafía se descubrió el pastel.

Lo más sorprendente es que Chasles no sospechara ni de la cantidad de manuscritos ni pusiera en duda escritos de Cleopatra redactados en francés.

EL TEOREMA FAROL 

Lamentablemente, el «último teorema de Fermat» es el nombre que se dio al farol de Pierre Fermat (1601-1665) cuando éste, trabajando con números enteros anotó en el margen de un libro de aritmética de Diofanto: Es imposible dividir un cubo en suma de otros dos o un bicuadrado en otros dos bicuadrados, en general una potencia cualquiera superior a dos en dos potencias del mismo grado; he descubierto una demostración verdaderamente maravillosa pero este margen es demasiado pequeño para contenerla. 

La excusa del angosto margen para alguien como Fermat, que era magistrado en Toulouse y estaba rodeado de miles de papeles, resulta inaceptable. En el fondo, o se equivocó al pensar una justificación o tuvo la mala fe de dejar la sospecha de si realmente lo había descubierto.

Cuando A. Wiles enunció en la década de los noventa que había resuelto el mítico teorema de Fermat, no contó con que su brillante demostración tuviera un gazapo. La suerte y la ayuda de Taylor permitieron que el dúo Wiles & Taylor lograra poco después la demostración perfecta. Después de esperar 300 años para que esto se demostrara, ya no importaba emplear unos meses más. Pero ya se sabe que, en matemáticas, o está bien del todo o no hay nada. 

NÚMEROS QUE ESPERARON SERLO 

Un error histórico monumental ha sido la reticencia en admitir la utilidad de nuevas clases de números. Los números negativos inventados por los chinos en contabilidad (siglo VIII) tardaron siglos en ser considerados «verdaderos números» en Europa. Incluso en tiempos de Descartes (siglo XVII) se hablaba de falsas soluciones cuando aparecían negativos. Los números imaginarios (como raíces de números negativos) ya llevan en su propio nombre de «imaginarios» lo que la gente pensó de ellos. 

UN CULPALBE LLAMADO DIONISIO 

El error mayúsculo del calendario cristiano tiene un nombre: Dionisio el Exiguo (470-550). Si bien el papa Juan I sólo le había pedido que determinara las fechas de Pascua, Dionisio fue más allá del encargo e hizo la propuesta de redefinir el inicio de la era cristiana en relación con el nacimiento de Jesucristo y abandonar la tradición de referir los años en relación al emperador Diocleciano. Pero Dionisio optó por fijar el 25 de diciembre para no alterar la tradición que (desde el siglo II) celebraba en esta fecha la festividad del dios Mitra. Y atendiendo a que el pueblo judío acepta al nacido en la congregación a partir de la circuncisión el octavo día después del nacimiento… resulta que Dionisio fijó el inicio de la era no el día de Navidad, sino el 1 de enero. Y además se equivocó al situar en el tiempo el verdadero nacimiento de Jesús. 

2010 = 5770 = 4707 = 1432

El mundo es global, la Coca-Cola está en todos sitios pero cada cultura sigue con su calendario, con su peculiar fecha de inicio de año y con una duración peculiar. Nuestro 2010 es el 5770 judío, el 4707 chino, el 1432 musulmán… un lío monumental de años y Nocheviejas. 

TANTOS ERRORES COMO CALENDARIOS 

La historia de nuestro calendario gregoriano es el resultado de una constante corrección de errores que fueron motivando la necesidad de cambios. En el siglo VII a.C., los romanos tenían un calendario de 304 días divididos en 10 meses, y el año se iniciaba en marzo. No funcionó: las estaciones no empezaban cuando debían. ¿Solución? Añadir dos meses: enero y febrero al final (!) de cada año, considerando meses uniformes de 30 días. Luego, con Julio César vino en el año 45 a.C. el calendario juliano, con 365 días más un cuarto de día, doce meses de días variables… y cada cuatro años un día extra (bisiestos). Este calendario juliano tenía un desfase de 11 minutos y 14 segundos respecto del año trópico terrestre, lo que daba sólo un error de 1 día en 128 años… pero los años pasaron, y en 1477 la primavera se había adelantado al 11 de marzo.

Preocupado por fijar las fechas (movibles) de Pascua, el papa Gregorio XIII instó a la creación de un nuevo calendario, nuestro calendario gregoriano, inaugurado en 1582, año en que el jueves 4 de octubre pasó a ser viernes 15 de octubre, corrección que permitió que la primavera del 1583 empezase el 21 de marzo. De nuevo un arreglo de bisiestos: lo serían los años con las dos últimas cifras divisibles por 4, excepto cuando ambas eran cero.

Pero si el número completo del año era divisible por 400, entonces seguro que era bisiesto (¡fue el caso del 2000!). Ahora el error de nuestro calendario ya es sólo de 1 día cada 3.226 años. ¿Le preocupa este error? 

LA COMPLEJIDAD DEL AÑO 

El concepto clave para medir los tiempos humanos y hacer calendarios que permitan predecir las estaciones ya se tambalea de entrada, pues el año solar o trópico tiene 365 días, 5 horas, 48 minutos y 46 segundos, lo cual ya hace prever problemas de temporalidad. Pero si a esto se añaden las fases de la luna, las fiestas religiosas movibles, los atrasos horarios bianuales… es fácil prever los muchos errores que en cualquier momento pueden cometerse.  

Las buenas propuestas —y el calendario gregoriano lo fue— se acaban imponiendo siempre en los lugares dispuestos a cambiar algo. Pero la decisión de un cambio de calendario no es tan simple y algunos países se lo tomaron con calma. Además, como el calendario era «católico», su validez en lugares «protestantes» fue algo no trivial. En Suiza (tierra de relojes) no acabó de cuajar un calendario válido para católicos y protestantes hasta 1701. En Inglaterra, que con eso de las reformas del continente siempre han ido atrasados (el Canal de la Mancha debe ser inmenso), esperaron hasta 1751. La siempre prudente espera nipona hizo que Japón no se adhiriera hasta 1873.

Este tema lleva a muchas dificultades matemáticas cuando se quieren datar acontecimientos históricos, pues según los países pueden aparecer referencias a calendarios distintos. Cuando lea «así, el 2 de abril de 1649…», pregúntese inmediatamente: ¿dónde? 

CRÓNICA DE UNA MUERTE ANUNCIADA 

El italiano Gerolamo Cardano (1501-1576), matemático y médico, se atribuía «el cultivo de las artes ocultas» y presumía de tener «facultades adivinatorias», pero llevó la cosa demasiado lejos y predijo el día de su propia muerte: el 21 de septiembre de 1576. Y así fue: este día se suicidó.

FECHAS QUE BAILAN 

En un popular libro de J. H. Conway y R. K. Guy (The book of numbers, Nueva York, Springer-Verlag, 1996) se hace referencia a una carta con un resultado aritmético enviada por el gran matemático Leonhard Euler el 15 de abril de 1706 a Christian Goldbach. Lo cual es sorprendente teniendo en cuenta que Euler nació el 15 de abril de 1707. Parece ser que el año correcto de la carta fue 1750. 

BARBEROS Y FALACIAS LÓGICAS

 Grave error pretender calcular siempre el grado de verdad o falsedad de lo que se dice. El gran lógico, matemático y filósofo Bertrand Russell (1872-1970) puso en evidencia lo paradójico que es intentar asignar valoraciones lógicas de verdad o falsedad a frases que predican algo sobre sí mismas. La forma popular de difundir la paradoja de Russell ha sido: «Un barbero es alguien que afeita a unos que no se afeitan ellos mismos y no afeita a los que lo hacen por su cuenta». ¿Qué ocurre con la barba del propio barbero? Si se afeita, está actuando sobre uno que ya se afeita por su cuenta, y si no se afeita, es que no actúa sobre uno que ha dejado su autoafeitado. O sea: el barbero no puede ni afeitarse ni dejar de afeitarse…

La famosa sentencia: «Esta frase tiene cinco palabras», ¿es cierta o falsa? Ojo: ni lo uno ni lo otro. ¿Y la afirmación «Yo miento»? Los disparates surgen en lógica cuando uno se obstina en buscar criterios de verdad o falsedad en sentencias que no son proposiciones susceptibles de análisis. ¿Acaso usted se atrevería a decir si la orden «Abre la puerta ahora mismo» es verdadera o falsa? Sólo Campoamor nos lo aclara bien con aquello de que la verdad y la mentira dependen del color del cristal con que se mira. ¡Pero no se fíe de las gafas! 

RIGOR RELATIVO 

A lo largo de la historia matemática, muchas han sido las nociones intuitivas que con el paso del tiempo han ido evolucionando desde una situación vaga hasta llegar a una descripción rigurosa. Si se dice a nivel popular: «Todos los hombres tienen lo que se merecen. Los demás son solteros», en matemáticas podría decirse: «Todas las épocas tienen el rigor que pueden». Calcular bien necesita muchos años de creatividad para gozar de criterios claros. El rigor evoluciona y acaba aclarando lo que era erróneo (aunque fuese intuitivo) y lo que se salva.

LA ATRACCIÓN POR CUADRAR EL CÍRCULO 

La cuadratura del círculo, es decir, partir de un círculo y construir con regla y compás un cuadrado de igual área, es algo que no puede hacerse. Por eso la voz popular cuando se enfrenta a un problema imposible de resolver (llegar a fin de mes con dinero, por ejemplo), clama: «Esto es como la cuadratura del círculo». Pues bien, a pesar de la voz popular y de los pacientes matemáticos que en su día demostraron que este problema no tenía solución, nada ha impedido que desde siempre hayan existido forofos del problema que ofrecen a quien quiera leerlo «su» cuadratura del círculo. Ha sido una auténtica plaga histórica de aficionados desacertados que han autopublicado sus notas, han molestado a las academias y las universidades, etc. Precisamente la negativa oficial es lo que los anima («Todos están equivocados. Yo tengo la solución»). Y como ningún académico serio está dispuesto a perder su tiempo en hallar el error, los fanáticos cogen nuevas alas: «Nadie me indica ningún error; por tanto, tengo razón».

El paciente y bondadoso matemático Underwood Dudley ha recibido tantas «soluciones» de la cuadratura que en una ocasión escribió: «El final de la cuadratura del círculo sólo será posible como consecuencia del final de la civilización». Dudley incluso ha escrito la obra Fanáticos matemáticos, en la que presenta su increíble colección personal y su correspondencia con todo tipo de locos que creen haber resuelto problemas imposibles de resolver (trisecar un ángulo, inscribir polígonos de siete lados, duplicar el cubo…) o haber encontrado demostraciones fáciles de resultados muy complicados… e incluso invenciones numéricas auténticamente locas. Un libro sobre errores que hace perder la confianza en la humanidad. 

MÁQUINAS CONTRA ERRORES 

Lo que más motivó desde el siglo XVI el invento de todo tipo de máquinas para calcular fue la evidencia de que «los tiempos avanzaban que era una barbaridad» y con cálculos cada vez más largos afloraban los errores en números en todos los momentos posibles: al escribirlos a mano, por los decimales considerados o no, al ser impresos con errores tipográficos, al operar con ellos, etc. 

LA MÁQUINA DE BABBAGE 

El genial Charles Babbage (1792-1871) logró dar un nuevo impulso a la automatización del cálculo inventando dos máquinas. La máquina de diferencias y la máquina analítica, que debían permitir el cálculo rápido y exacto así como su impresión. Pero estas máquinas, por su complejidad (la de diferencias debía medir 1 m × 2 m × 2,5 m y tener 25.000 piezas) no pudieron ser nunca construidas en vida de su inventor, a pesar de gastar en ellas su fortuna personal y buenas subvenciones gubernamentales. Aquí Babbage calculó mal sus posibilidades, pero dejó abierto el camino a la computación del siglo XX. Lo que importa es avanzar. Como dijo Babbage, «los errores derivados de usar datos equivocados son menos importantes que los que se cometen sin usar ningún dato». 

LOS PROGRAMAS DE ADA 

Ada Lovelace (1815-1852) fue una ilustre matemática hija del poeta lord Byron y colaboradora de Charles Babbage. Fue la primera programadora de la historia, y la actual programación informática la reconoce como pionera. Lástima que se equivocó de época y sus programas no encontraron máquinas que pudieran ejecutarlos. 

TEOREMAS PENDIENTES DE VEREDICTO 

2 + 2 = 4, pero cuando sube el nivel matemático de las cuestiones puede no ser inmediato decidir si un resultado nuevo esconde algún error o es realmente nuevo o si, además de correcto, es interesante. Muchos resultados matemáticos son hoy tan sofisticados y usan tantos resultados previos que no es en absoluto trivial decidir su total veracidad, es decir, si ha nacido un nuevo y brillante teorema o si se trata de un intento con algún error u omisión aún pendiente de subsanar (si se puede). El autor (o autores) está convencido de la bondad de su resultado, pero entonces sólo algunos grandes especialistas en un tema tan especial pueden intentar comprender lo que se ha hecho. Pueden necesitarse varios meses antes de que el veredicto de los más sabios sea positivo y aquello se publique. Pero aún puede quedar la duda de si realmente los sabios no fueron sabios despistados.

Los grandes resultados matemáticos nuevos necesitan, pues, no sólo la creencia de sus autores, sino la bendición de la comunidad. 

ELEGANCIA MATEMÁTICA 

El eminente matemático George Pólya se atrevió a dar una fórmula para decidir si un teorema de geometría era «elegante». Según Pólya: La elegancia es directamente proporcional al número de ideas que en ellos vemos, inversamente proporcional al esfuerzo requerido para comprenderlas. Como frase es curiosa. Como cálculo es imposible, porque evaluar el esfuerzo de comprensión no sabría hacerlo ni el mismo Pólya.  

UNA DEMOSTRACIÓN QUE SÓLO DURÓ ONCE AÑOS 

Ésta es la curiosa historia de un abogado que «resuelve» un gran problema matemático y durante 11 largos años nadie supo advertir que la solución era falsa. En 1852 Francis Guthrie, observando mapas, tuvo la intuición de que con cuatro colores era posible colorear estas configuraciones de forma que zonas con frontera común tuvieran colores diferentes. Francis mandó una nota sobre esta curiosa cuestión a su hermano Frederick, que por aquel entonces seguía un curso de Augustus De Morgan. No sabiendo dar una respuesta, De Morgan fue explicando este problema a otros colegas como sir William Hamilton. Fue Arthur Cayley quien en 1878 llegó a presentar formalmente este reto a la London Mathematical Society, con lo que este problema quedó abierto a la consideración de todos. 

En 1879 surgió por sorpresa la publicación de un artículo en el que demostraba que, en efecto, cuatro colores eran suficientes con una ingeniosa explicación hallada por Arthur B. Kemper, un abogado de Londres. Entre 1879 y 1890 (¡once años!) la solución de Kempe se dio como buena y por tanto el problema de los cuatro colores se consideró resuelto.

La sorpresa surgió en 1890, cuando P. J. Heawood puso en evidencia un fallo (no resoluble) en la solución de Kempe y otra vez el problema quedó pendiente de solución. El propio Heawood y muchísimos otros dedicaron entonces muchos años y muchos esfuerzos a intentar probar la certeza del resultado. Nadie pudo encontrar nunca un mapa que necesitara como mínimo cinco colores… Por tanto, era lógico apostar por la validez de que con cuatro colores debía ser suficiente.

Fue entre 1970 y 1976 que los matemáticos Kenneth Appel y Wolfgang Haken, de la Universidad de Illinois en UrbanaChampaign, con la ayuda de un computador y distinguiendo miles de casos lograron dar la buena nueva:

«Cuatro colores son suficientes»

DEMOSTRACIONES INCOMPLETAS 

Muchísimos ejemplos históricos muestran que matemáticos eminentes han descubierto una propiedad pero que en la primera demostración que han dado han olvidado justificar algún detalle o algún caso especial. Un tiempo después (¡pueden transcurrir años!) otro matemático lo ha revisado y ha logrado completar lo que faltaba.

Por ejemplo, Adrien-Marie Legendre logró ver cómo eran los números enteros positivos que se podían expresar como suma de tres cuadrados… pero la demostración completa no llegó hasta que Carl Friedrich Gauss subsanó el gazapo de Legendre. 

ERRORES QUE PERMITEN PUBLICAR MÁS 

En el mundo actual de la matemática universitaria se valora muchísimo el número de artículos publicados por los profesores, lo cual ha llevado al popular lema americano del «publica o perecerás». En este contexto es popular la pregunta que dice: ¿Qué es mejor, publicar un solo artículo sin errores o un artículo con un error? Lo increíble es que si alguien logra publicar un trabajo con un error e inmediatamente manda otro artículo con la corrección, gracias al error tiene «dos publicaciones» y no sólo una. 

¿DÓNDE CABRÁN LOS MATHEMATICAL REVIEWS? 

Hace muchos años la American Mathematical Society inició la gran labor de editar los Mathematical Reviews, recensiones cortas de todos los artículos y publicaciones matemáticas. Pero los volúmenes mensuales de estas recensiones fueron aumentando el número de páginas y las estanterías de los despachos de los muchos matemáticos que recibían estos volúmenes se fueron colapsando. Cálculos catastróficos sobre el crecimiento de estos volúmenes auguraban que no sería posible leer lo publicado ni tan sólo guardarlo. Nadie pudo prever que muchos años después el problema desapareció totalmente. Internet lo resolvió. Fue un error creer que la información sería imposible de acumular. Lo que falta ahora es tiempo para leerla. 

CREACIONISTAS Y PROBABILIDAD 

La evolución de la vida en el planeta Tierra viene bien avalada por procesos físicos y químicos. No obstante, el sector de los creacionistas sigue insistiendo en la «creación» milagrosa, aportando a menudo argumentos probabilísticos erróneos y disparates estadísticos de gran magnitud. El que un acontecimiento sea muy improbable (por ejemplo, lanzar 1.000 monedas y que salgan 1.000 caras) no quiere decir que en la primera tirada de las 1.000 no pueda darse. Una cosa es la improbabilidad y la otra la ocurrencia. Y ahí está uno de los talones de Aquiles de los creacionistas. 

MARKETING TEÓRICO 

La idea de «vender» bien las expectativas de una teoría matemática ha incorporado a veces denominaciones malévolas sobre las que desarrollar el marketing del tema. Así, René Thom acuñó el término «teoría de catástrofes» para un interesante estudio de puntos especiales en superficies. Poca gente hubiese prestado atención si aquello se hubiese denominado de forma estrictamente académica, pero lo de «catástrofes» causó un gran impacto. La gente entendió que aquel nuevo cuerpo doctrinal iba a permitir evitar catástrofes naturales (epidemias, terremotos, tsunamis…), hasta que pasados unos años se vio que, «de evitar», nada de nada.

EPÍLOGO

Los disparates matemáticos tienen asegurado un futuro aún más prometedor que su pasado. Seguirán conviviendo con todos nosotros y formando parte de la cultura popular. Ante este hecho, lo más aconsejable es que no perdamos nunca el espíritu reflexivo. Con poética resignación hindú, ya Radindranath Tagore nos recordó que: 

"Si cierras la puerta a todos los errores, también la verdad se quedará fuera" 

A la vista de todo ello y siendo positivos, podemos vivir con la esperanza que indicó John Kenneth Galbraith: 

"Aunque todo lo demás falle, siempre podemos asegurarnos la inmortalidad cometiendo algún error espectacular"

DISPARATES MATEMATICOS DE POLITICOS

El jardín frondoso y exuberante de los disparates matemáticos y toda la tropa de sus jardineros ha ofrecido un voluminoso ramo de situaciones sobre las que he podido seleccionar su material. La popular definición del político británico conservador lord Richard Austen Butler «La política es el arte de lo posible» ya hace presagiar que entre este elenco de artistas serán abundantes los disparates matemáticos de todo tipo. Ya lo comentó el escritor inglés J. K. Jerome: 

"La mejor política consiste en decir siempre la verdad, salvo, claro, que tengas una excepcional capacidad para mentir"

La historia está sembrada de vistosos ejemplos protagonizados por políticos que ya sea por analfabetismo numérico, por pobre digestión de datos, por mala fe en interpretaciones de estadísticas o por promesas alocadas, han hecho bellísimas aportaciones a este sugestivo mundo de los disparates. ¡Y siguen en la brecha! Pero de la misma manera que detrás de un hombre que triunfa hay siempre una mujer sorprendida, detrás de todo político hay siempre un equipo de asesores que respaldan sus intervenciones y que a menudo son los creativos de los errores.

Curiosamente, los grandes fallos numéricos hacen crecer como la espuma la popularidad del personaje que los comenta, lo cual lleva al interesante método de buscar intencionadamente disparates que puedan ser portada de diario o noticia audiovisual. Y desde You Tube a los medios de comunicación actuales se presta a menudo una ayuda (¡inestimable electoralmente!) para difundir con especial énfasis precisamente el desliz (fortuito o malévolamente preparado).

El propio Napoleón Bonaparte ya decía:

«No interrumpa nunca a su enemigo cuando está cometiendo un error».

Posiblemente si hubiese nacido muchos años después y cambiara batallas por telenoticias y enemigos por entrevistados, Napoleón hubiese podido ser un gran periodista político. 

EL TEOREMA DE ZAPATERO 

En 2009, en plena discusión sobre la financiación de las autonomías españolas, el presidente del gobierno José Luis Rodríguez Zapatero (para intentar contentar a todos) anunció lo que el político catalán Artur Mas calificó acertadamente como «el teorema de Zapatero». Dicho teorema, equivalente a la cuadratura del círculo, decía: 

"Todas las comunidades quedarán por encima de la media" 

Es totalmente imposible que una media entre cantidades sea superior a todas ellas: la media de 4 y 6 es (4 + 6) / 2 = 5, entre el 4 y el 6. En todos los promedios habrá siempre números menores y mayores. Pero la afirmación del funesto presidente podría contener un mensaje subliminal cierto: si todas las cantidades son iguales, entonces éste es el valor de la media, es decir, el teorema de Zapatero sería una forma barroca de anunciar el «café para todos». 

TANTOS POR CIENTO VISTOS POR LULA 

Al acercarse el final del segundo mandato presidencial de Lula da Silva, en Brasil se realizó una encuesta sobre cómo vería la población la posibilidad de que, con los oportunos cambios legislativos, el popular presidente pudiera presentarse para un tercer mandato. El resultado fue que el 60 % opinó desfavorablemente. Pero lo sorprendente del caso fue que al ser preguntado el propio presidente Lula sobre qué opinaba de este 60 % en contra, en un alarde de modestia declaró: 

El resultado ha sido del 60 %, pero si me hubiesen preguntado a mí hubiese sido del 61 % 

No es creíble que Lula da Silva considere su opinión personal equivalente al 1 % de la colosal población brasileña. Por tanto, es más verosímil que su dominio de los porcentajes no sea su especialidad (lo cual —dicen— le hace aún más popular entre su electorado). 

LA JUVENTUD DE MENEM 

El carismático presidente argentino Carlos Menem, que una vez divorciado de su primera esposa se casó con una atractiva presentadora de televisión chilena, en su (infructuoso) último intento de volver a presentarse a las elecciones presidenciales tuvo la osadía de intentar esconder su edad. Aunque las arrugas de su cara, de su cuello y de sus manos eran más evidentes que cualquier número, Menem, para autoproclamarse más joven, usó este ingenioso argumento: 

Uno tiene la edad de la persona a la que ama.

 Con ello consagró esta moda de hombres lamentablemente mayores que acaban acompañados (temporalmente) por jóvenes esposas.

TIEMPOS ORIENTALES

La acreditada paciencia oriental hace posible que las percepciones temporales asiáticas sean muy generosas. Cuando un periodista preguntó al primer mandatario chino que visitó oficialmente Francia qué opinaba de la Revolución francesa, el interpelado respondió: 

Aún no ha pasado el tiempo suficiente para emitir una opinión

O no sabía de historia o bien le falló su aritmética, porque 200 años parece un tiempo más que razonable para tener ya una opinión formada. Estaremos a la espera. 

EL MODELO ATÓMICO DE FIDEL CASTRO 

El famoso líder cubano Fidel Castro quiso en una ocasión evaluarse a sí mismo. En lugar de decir «no me arrepiento de nada» o «no tengo una pizca de arrepentimiento», introdujo una novedosa forma de evaluación: 

He cometido errores, pero ninguno estratégico, simplemente táctico […]. No tengo ni un átomo de arrepentimiento de lo que hemos hecho en nuestro país. 

El arrepentimiento es ahora atómico.

MARIANO RAJOY COMO CALIBRADOR 

Una de las apreciaciones de peso más espectaculares fue realizada por Mariano Rajoy (siendo vicepresidente del Gobierno en 2002) cuando, al describir la salida de 125 toneladas diarias de crudo del hundido barco Prestige por sus 14 fisuras, aportó la descripción

salen como hilitos de plastilina

EL SENTIDO GEOMÉTRICO DE FRANCO 

Francisco Franco aportó a las antologías de errores la inestimable perla (a su esposa las perlas le gustaban mucho): 

Estábamos al borde del abismo y hemos dado un paso al frente

lo cual demuestra un alto sentido de autocrítica… o un desliz propio de un suicida.

LAS PONDERACIONES DE BUSH 

La finura matemática del que fue presidente de Estados Unidos, George Bush, no ha sido precisamente envidiable. Durante sus ocho (largos) años de mandato, Bush no cometió grandes «errores» numéricos explícitos (porque nunca incluyó cifras en sus discursos) pero sí puso en evidencia que sus conceptos cuantitativos no eran muy claros. Por ejemplo, cuando afirmó: 

Un número bajo de votantes es una indicación de que menos personas están yendo a votar

evidenció una confusión entre abstención y votos dados a una opción. La geometría tampoco parece ser su especialidad:

El gas natural es hemisférico. Me gusta llamarle hemisférico en la naturaleza, porque es el producto que podemos encontrar en el vecindario.

¿Gas en el barrio? ¿Qué tiene de hemisférica esta fuente de energía? Una apreciación estupenda fue su convicción en la afirmación:

La gran mayoría de nuestras importaciones vienen de fuera del país

lo cual parecía indicar que había «importaciones» desde el propio país. ¡Algo inaudito! Y lo que ya le otorga poderes mágicos es su famosa frase:

Estoy atento no sólo a preservar el poder ejecutivo para mí, sino también para mis predecesores

ZAPATERO DA MÁS DE LO PROMETIDO

Al principio de la primera legislatura de José Luis Rodríguez Zapatero, el presidente español prometió que en los próximos cuatro años se iba a duplicar el presupuesto estatal dedicado a investigación. Y no sólo cumplió lo dicho sino que fue más allá y superó con creces el doble de euros dedicados a este importante fin. El motivo de superar lo prometido fue un error elemental de cálculo de los responsables de confeccionar y administrar los presupuestos, pues consideraron que para llegar al aumentar en 4 años el 100 % de lo dedicado a investigación debía aumentarse cada año al 25 %… Y afortunadamente para los investigadores así se hizo (y nadie protestó). Obviamente, al aplicar sucesivamente cada año el 25 %… del año anterior se fue mucho más allá del 100 %. 

MÁRGENES DEL PSOE Y EL PP 

En las continuas encuestas políticas sobre intenciones de voto en un momento dado, los estudios estadísticos dan a menudo resultados muy ajustados entre PSOE y PP. Pero el partido que obtiene un porcentaje mayor (43 %) se apresura a cantar su avance imparable y a humillar al otro (41 %):

«Ya llevamos más de dos puntos de diferencia».

Si hay suerte, y la encuesta se acompaña de una ficha técnica, usted podrá ver la muestra consultada, el lugar, el día de la consulta… y podrá leer siempre una frase del estilo: Margen de error: para un intervalo de confianza del 95,5 % y para p = q = 0,50, el margen de error es de ±3 %. Olvídese del tecnicismo del 95,5 %, de la p y de la q y fije su mirada en el ±3 %. El partido que saca el 43 % quiere decir que hoy obtendría entre el (43 – 3) % y (43 + 3) %, o sea, entre un 40 y un 46 %. Y el que saca 41 % obtendría entre (41 – 3 %) y (41 + 3) %, o sea, entre el 38 y el 44 %. Cualquier ganador es pues posible.  

UNA INFLACIÓN DEL MIL POR CIEN 

¿Es posible que la inflación galopante de un país pueda llegar en un año al 1.000 %? La respuesta es sí, y hace unos años ocurrió, por ejemplo, en Perú. ¿Puede el presidente que no controla este crecimiento brutal de la inflación volver a recibir la confianza de su país para otro mandato posterior? La respuesta es sí. Ocurrió en Perú, y años después Alan García volvió a ser presidente. 

SUPERFICIES Y MANIFESTACIONES 

Un clásico en los errores de «contabilidad» es el de las diferencias sorprendentes de diferentes fuentes sobre el número de manifestantes. Al habitual «400 según la guardia urbana, 10.000 según los organizadores», se ha añadido ahora en las consideraciones políticas la contabilidad de grandes manifestaciones («2.000.000 según los organizadores, 407.000 según la policía»). En el caso de Madrid, hoy estas macroconcentraciones son evaluadas por los organizadores, por la policía municipal, por los servicios de la comunidad, por el diario El País y por los blogs. La diversidad de cifras está servida. Afortunadamente diversas webs de internet dan alternativas fiables a los datos diversos de las manifestaciones www.malaprensa.com; www.manifestometro.blogspot.com; www.contrastant.net…) y el programa Sigplac del Ministerio de Agricultura, Pesca y Alimentación (http://sigpac.mapa.es/fega/vsiro/) permite medir bien superficies.

Es evidente que nunca podrá darse una cifra exacta, a no ser que se numere a los protestantes como en las maratones populares. También es evidente que toda la gente que circula, mira o está en el lugar de la marcha sin participar es difícil de descontar. Pero para una buena evaluación es suficiente calcular aproximadamente la superficie en metros cuadrados de calles y plazas ocupadas y multiplicar por 4 personas (máximo 6 en casos de auténticas aglomeraciones en una plaza). 

EL OLÍMPICO AZNAR 

Memorables quedan para la historia las sensibilidades medidoras de los presidentes Bush y Aznar cuando el primero presumió de correr 4 km en 6 minutos y 45 segundos y el segundo anunció que hacia los 10.000 metros en 5 minutos y 10 segundos. Seguramente por ello los dos llegaron tan lejos. El presidente Aznar también dejó para la teoría de números el nuevo concepto de «cero patatero».

DEFINICIONES Y MEDIDAS 

Nada resulta más absurdo que dar «medidas» de cosas hoy por hoy no medibles (felicidad, salud, suerte…). Pero es aún más alarmante cuando aparecen diversas medidas de una cosa que dependen, cada una, de la «definición de partida». Un caso socialmente relevante es el del paro. Se dan datos oficiales del INEM, se hacen encuestas a pie de calle… pero ¿cuál es la definición de «estar parado»? Si bien el concepto puede precisarse como persona que habiendo trabajado y cotizado ha perdido el empleo, pueden aparecer dudas de otra índole. ¿Se contabilizan las monjas de clausura, o se consideran una fuerza laboral con contrato eterno? ¿Y los que aún no han tenido ningún empleo? ¿Y los que ni tuvieron ni quieren empleo y viven en la calle? ¿Y los que trabajan cobrando en negro? ¡Dime la definición y haremos la medida!

LA INFLACIÓN DE LOS DATOS 

De la misma manera que los organizadores de manifestaciones tienden a sobrevalorar el número de asistentes, también muchos otros colectivos tienden a sobrevalorar su situación económica, o los valores de pobreza o el número del propio colectivo, etc. Gobernantes eufóricos en campaña electoral, ONG que buscan fondos, iglesias que recuentan feligreses… multiplican sus números por factores ambiciosos. Y como en el caso de los manifestantes, el problema es que no siempre es posible disponer de números fiables de referencia para discutir cifras. 

DISPARATES MATEMÁTICOS Y SALUD 

Una persona sana es un enfermo mal diagnosticado

El poeta y ensayista británico W. H. Auden afirmó en su día que «la salud era el estado sobre el cual la medicina no tenía nada que decir» pero en contraposición, el prestigioso doctor y político Josep Laporte proclamó que «una persona sana era simplemente un enfermo mal diagnosticado», lo cual nos coloca a todos, sanos y enfermos, bajo la tutela médica. Admitida la complejidad de la vida humana y la fragilidad del concepto de salud, es normal admirar la actividad diagnóstica o quirúrgica de la clase médica, a pesar de que, para Voltaire: 

Los doctores son personas que prescriben medicinas de las que saben muy poco, para curar enfermedades de las que saben aún menos, de seres humanos que desconocen 

Pero asumiendo que la medicina no es una ciencia exacta, es innegable que las matemáticas forman parte de las dosis de medicamentos, de los resultados de los análisis, de las gráficas sobre temas de salud, de las evaluaciones estadísticas y probabilísticas, de la tecnología creciente que ayuda al diagnóstico o al tratamiento… y entonces errores de cálculo o de concepto pueden tener sus efectos. Pero en dichos errores también pueden incurrir enfermeras, administradores de hospitales, autoridades sanitarias… y los propios enfermos con automedicaciones o malentendidos. 

¿QUÉ ES LA VIDA? 

Aunque la respuesta nos parece a todos evidente, no han faltado profesionales de distintas especialidades que han aportado una total confusión al tema: es un paraíso, es un cuento, es un instante, es un viaje, es una ilusión. ¡Viva la literatura! Pero seguro que la definición más precisa y con números es la siguiente:

Enfermedad de transmisión sexual con un 100 % de mortalidad

POPEYE Y EL MITO DE LAS ESPINACAS 

A principios del siglo XX, el doctor J. Alexander analizó el hierro en las espinacas y determinó un contenido de 0,003 gramos en 100 gramos de este vegetal, cantidad a todas luces ridícula para los consumidores. Pero un error de transcripción hizo que se publicaran 0,03 gramos en lugar de 0,003. A la sombra de estos datos fue inventado en 1929 el popular Popeye, que contribuyó a extender el mito del mucho hierro —y energía— que las espinacas aportan a nuestros cuerpos.

Hasta 1937 no se recalculó de nuevo el contenido de hierro de las espinacas. Según el químico Claudi Mans, para obtener los 14 miligramos de hierro que el cuerpo necesita a diario serían precisos 470 gramos de espinacas si este vegetal fuera totalmente asimilable. Pero como al comer las verdes hojas sólo se asimila un 2 % de lo anunciado, resulta que deberíamos ingerir 23,5 kilogramos de espinacas al día para asegurar la jugada. Imposible reto con espinacas pero fácil de lograr combinando carne, huevos, cereales, lentejas, embutidos, etc. 

TRISCADECAFOBIA 

Un disparate vivencial es tener «fobia» a un número. El mundo de las fobias afecta a millones de personas que por algún motivo tienen miedo a las cosas más diversas: a animales, a la música, a la altura, a la muerte, a la soledad… Basta mirar en la completa web http://www.fobias.net/M para darse cuenta de la variabilidad del tema y prever la creciente prosperidad de psicólogos y de todo tipo de terapeutas para intentar ayudar a superar estas fobias. Lo que es más sorprendente es que se incluya en este mundo fóbico la «triscadecafobia» o miedo al número 13.

Desde hace muchos años el numerito 13 se ha asociado a la mala suerte con absurdas eliminaciones de filas 13 en aviones o pisos 13 en hoteles, etc. Si los martes 13 son nefastos para nosotros, para los italianos el problema aparece los viernes 13, fechas también fatídicas en temas de virus de ordenadores que se activan estos días. Las leyendas y tradiciones culturales han dado mala fama al 13, mientras que han encumbrado positivamente a otros números, como el 3 o el 7. Pero que de una mala fama se pase a una fobia y al sofá de confesiones íntimas, hay todo un abismo. 

DOS TERCERAS PARTES 

No es un chiste, aunque lo parezca. Una paciente, al realizar una consulta telefónica con su doctor para determinar qué dosis debía tomar de unas pastillas, el prestigioso doctor (con más de cuarenta años de experiencia) le dijo:  

Le conviene aumentar la dosis. En lugar de media pastilla tome dos terceras partes

Siendo ella matemática y sabiendo que aquellas pastillas tenían sólo una rayita que marcaba la mitad, rápidamente insistió en que no sería fácil tomar las dos terceras partes. Pero la sorpresa vino con la respuesta médica:  

Señora, no hay ningún problema en tomar dos terceras partes: divida la pastilla por la mitad y luego tome una de las mitades y divídala de nuevo por la mitad. Ya tendrá tres trozos y se toma uno grande y uno pequeño, es decir, dos de los tres.

Inútil fue el intento de ella para hacer ver que ½ + ¼ = ¾, cantidad superior a 2/3. 

EL MISTERIOSO 0,0 % CERVE(CERO) 

Decimales del tipo 0,1 %, 0,02 %, etc., son normales. Y el 0 % es contundente. Pero hoy proliferan cervezas «sin alcohol» que, a pesar del radical «sin», no optan por el 0 % sino por el 0,0 %. Francamente curioso. Lo único matemáticamente razonable es intuir que el 0,0 % es el resultado de truncar una expresión del tipo 0,0X % para así poder pasar del «poco» al «sin». Estudios sobre diversas marcas hacen ver que, en efecto, éste el caso (Bavaria 0,04 % vol.; Buckler 0,05 % vol.; San Miguel 0,03 % vol., etc.), aunque en la generación del «sin» también existen los valores 0,85 % vol. (Laiker), 0,95 % vol. (Kaliber), 1,1 % vol. (Ambar Green), 0,85 % vol. (Damm Bier), etc. Todas tienen en efecto bajísimos niveles alcohólicos pero, matemáticamente, lo del «sin» y «0,0 %» son engañosos. 

LA INVASIÓN LIGHT 

A partir del acuerdo de 1990 de la Comisión Interministerial para la Ordenación Alimentaria, se maneja en España la siguiente: Definición. Un alimento puede ser calificado de light si y sólo si cumple con los siguientes requisitos: 

(i) Para que exista un light debe existir en el mercado su homólogo no-light.

(ii) Debe haber un 30 % de reducción mínima del valor energético respecto del alimento de referencia no-light.

(iii) Debe tener un etiquetado explícito sobre reducción de calorías y valor energético (por 100 g o 100 ml) con referencia al homólogo no-

light. 

La más curiosa es la condición (i), pues impide la denominación light a un producto si el mercado no ofrece otro nolight, es decir, lo de light es «relativo» y no una condición autónoma. Para lograr las versiones light hay dos trucos elementales: o usar edulcorantes (sorbitol, manitol, xilitol, sacarina, aspartame, ciclamato, etc.) en lugar de azúcar (sacarosa) o fructosa, o bien sustituir grasas por otros elementos que simulen sabor y características pero disminuyan calorías.

La cifra relevante en el mundo light es el aludido 30 % de reducción mínima de aporte de calorías (reducción a un tercio menos de calorías o mitad de grasa en la ley norteamericana). Educados con el Lazarillo de Tormes y dotados de una capacidad olímpica para saltarse a la torera cualquier definición, cualquiera puede imaginarse la picaresca en el mundo light. La primera es no usar la palabra y dar otras denominaciones que para el consumidor signifiquen lo mismo pero que libren al producto de reglamentaciones. Ahí están los «bajo en grasa», «sin azúcar», «0% materia grasa», «diet», «ligero/a», «desnatado/a», «bajo en calorías», «+ fibra – grasa» y un sinfín de alternativas. Generalmente, como lo light o equivalente parece exigir más esfuerzo, surge el siguiente teorema: 

Todo producto light tiende a ser más caro (76 %) que su producto homólogo no-light 

UN ESTUDIO LIGHT… ESCALOFRIANTE 

Los estudios de Eroski realizados recientemente sobre 52 alimentos light fueron realmente alarmantes al presentar los siguientes problemas: todos los etiquetados eran deficientes, tres de cada cuatro eran más caros «por ser light» y la tercera parte de los light no lo eran, pues no alcanzaban la reducción del 30 % calórico respecto de sus versiones no-light. El siguiente párrafo del estudio Eroski es concluyente: "Según concluye el estudio, no son light ninguno de los alimentos estudiados de cereales «tipo línea» para desayuno (Kellog’s Special K y Nestlé Fitness), chocolates (Santiveri Fondant, Pagesa Fondant), patatas fritas (Celigüeta light y Matutano light), galletas (Gullón ligeras y Lú Vitalínea), leche condensada (Nestlé), nata líquida (Central Lechera Asturiana Cocina ligera), pan tostado (Recondo sin sal y sin azúcar, y Recondo sin grasa y sin sal) y pan de leche (Martínez integral «– grasa»). Asimismo, tampoco son light uno de los batidos de leche (Central Lechera Asturiana, «vainilla bajo en grasa») incluidos en el informe y una de las mermeladas (Vieja Fábrica «fresa diet»").

Para colmo, los alimentos no-light pero sí «diet», «menos…», «sin…» pueden ser incluso más energéticos y dar más calorías que sus homólogos «más…», «con…». Valgan de referencia mermeladas sin azúcar pero con fructosa o determinadas leches condensadas, chocolates, etc.

AL FINAL, ¿TODOS JÓVENES? 

Algo que resulta hoy extraordinariamente borroso es el tramo de edades que corresponde a la juventud. Como «ser joven» aparece siempre como algo deseable, multitud de ochentones se declaran jóvenes y no hay actriz o actor que renuncie a serlo. La cirugía plástica promete mantener aspectos juveniles y un amplio grupo de la población desea situarse «entre los jóvenes» para beneficiarse de determinadas ventajas, descuentos, acceso a vivienda, etc.

Hoy los populares carnets de jóvenes llegan a los 30 años, e incluso los prestigiosos premios matemáticos de las Medallas Fields admiten sólo a jóvenes matemáticos hasta los 40 años. Las informaciones periodísticas o programas de ayudas hacen a menudo referencia a «jóvenes de entre 15 y 29 años»… Un auténtico lío entre el número de años y el concepto juventud. El error es empeñarse en identificar el concepto borroso «juventud» con un rígido intervalo temporal. Es más razonable lo que se hace en lógica borrosa al introducir «grados» de juventud, superando la bestial contraposición clásica de o joven o viejo. 

PREVISIONES DE LONGEVIDAD 

Con jubilaciones entre los 60 y los 70 años pero con esperanzas de vida crecientes, las personas deberíamos pensar que las previsiones temporales deben ser de entre 20 y 30 años… y todo lo que ello implica de previsión de dinero necesario. El cálculo para el primer mes de jubilación es simple, pero prever poder pagar una residencia al cabo de 15 años ya no es un tema trivial. Nuestra esperanza de vida nos debe inducir a no cometer el error de mirar sólo a corto plazo. 

ÍNDICE DE MASA CORPORAL 

Justo cuando ya todo el mundo había logrando aprenderse aquello de que lo conveniente en cuanto al peso es que el número de kilogramos sea equivalente al número de centímetros en que la altura supera al metro («si mide 1,70 metros, pese unos 70 kilos»), surgió la gran familia de médicos y especialistas en peso y aconsejó que se usara como indicador el índice de masa corporal: IMC = peso en kilogramos/(altura en metros)2. El nuevo índice debía situarse entre 20 y 25, con la recomendación de no superar el 25 (zona de sobrepeso) ni quedarse debajo del 20. Los especialistas esconden el hecho de que toda persona que cumpla con la vieja regla de peso y centímetros seguro que tiene bien el índice.

Pero lo remarcable de la historia es que al incluir el IMC en el denominador un cuadrado, la difusión de la formulita en los medios de comunicación se vio expuesta a todo tipo de desconsideraciones. En algunos periódicos no aparecía el cuadrado, en otros aparecía el 2 del cuadrado multiplicando a la altura, y otras revistas ni tan sólo se atrevieron a dar una fórmula «tan compleja» y facilitaron tablas de doble entrada (peso/altura) donde moviendo los dos dedos se podría hallar el IMC correspondiente. En el periódico La Vanguardia se dedicaron dos páginas a salud y obesidad, y cómo no, apareció el dichoso índice de masa corporal. Se daba la fórmula: 

Talla × talla / peso = IMC 

Recordando que la normalidad se sitúa en un IMC entre 20 y 25, se invita al lector a que haga sus cálculos. ¡Increíble! Nadie llega a normal. La fórmula está invertida: al ir aumentando de peso, iría disminuyendo el índice. 

UNA FÓRMULA PARA LA MORTALIDAD 

El matemático Abraham de Moivre, cuya obra ha sido muy útil en cálculos de seguros, fue el primero que dio una fórmula para evaluar el número de personas vivas V(x) a una edad x si P era la población considerada: 

V(x) = P·(86 – x)/86

si la edad x era menor que 86, y V(x) = 0 si x era mayor de 86. Siendo la fórmula de 1715, es razonable pensar que De Moivre considerara los 86 años como un límite muy elevado de supervivencia. Hoy sería más avanzada. Lo que hoy sería una fórmula errónea vistos los datos actuales, era en 1715 una buena descripción. La leyenda dice que el propio De Moivre predijo (y no erró) el día de su muerte: 27 de noviembre de 1754; de mayor se dio cuenta de que cada día dormía 15 minutos más que el día anterior, lo cual le llevó al cálculo del día en que dormiría 24 horas y, por tanto, moriría. Y murió. 

MENOS CÁNCER, MÁS MALARIA 

Eliminar riesgos para la salud es siempre una labor meritoria, pero debe evaluarse si la supresión de un riesgo pequeño no puede llevar a la aparición de riesgos mayores. Ocurrió hace poco en Indonesia, donde se empezó a eliminar el uso de pesticidas en los cultivos, pues podían influir en al aparición de cánceres. Aunque los riesgos eran pequeños, se optó por evitar su posibilidad. Pero no se contó con que la desaparición de pesticidas permitió un aumento notable de mosquitos, y con ellos, los casos de malaria, enfermedad de graves consecuencias en aquellas latitudes. El error de no usar datos indicadores de las consecuencias de una determinada acción puede llevar a este tipo de problemas. 

¡GALLETAS NO! 

Imaginemos una fiesta familiar donde se entabló una discusión notable entre el nonagenario AC y sus dos hijas. El venerable anciano de 97 años quería comer dos galletas rellenas que eran sus predilectas, pero sus dos hijas (jubiladas) se negaron a llevárselas aduciendo que debía seguir el régimen estricto impuesto por el doctor. Tuvo suerte pues un nieto se levantó y le dio las galletas con el argumento de que a la edad del abuelito éste bien podía permitirse este capricho. Esta historia pone en evidencia la necesidad de evaluar las acciones de riesgo mínimo que, aun transgrediendo la ortodoxia médica, contribuyen al bienestar emocional. ¿Cuántos días de vida podía perder el abuelito por las dos galletas? 

PLACEBOS ESTUPENDOS 

Es un error no fijarse en los datos estadísticos que avalan la importancia que tiene la actitud y la fe del paciente ante determinados fármacos o médicos. Medicamentos que no tienen nada (quizás sacarina o hierbas), pero perfectamente preparados, que son caros y son recetados por un doctor, pueden provocar que pacientes que creen en ellos noten mejorías ostentosas. Se ha calculado que hasta un 40 % de los pacientes pueden mejorar con placebos. Los misterios del cuerpo y de la mente son siempre sorprendentes.

Entre la clase médica destacan con luz propia los llamados «médicos placebo», es decir, profesionales de la medicina que aun aplicando iguales tratamientos que otros colegas, gracias a su personalidad logran mejores efectos en los pacientes. Su mítica competencia hace que la fe de sus pacientes en ellos sea muy superior a la normal, y ello afecta positivamente a su salud. Así cabe interpretar la conocida frase del afamado psiquiatra Dr. Sarró que hace años dijo a otro médico: 

Sí, todo lo que usted quiera, pero cuando yo receto Trofanil curo más que usted

Aunque el efecto es difícil de explicar, en este caso lo curioso es que no haya ranking ni números informando de estos doctores. Usted sabe la quinta canción más vendida del verano, pero ignora cuál es el tercer psiquiatra con más éxitos médicos del año. 

EL SEXO Y LAS VOLUNTARIAS ESTADÍSTICAS 

El famoso estudio The Hite Report de 1976 sobre las actitudes femeninas en temas sexuales, que tuvo gran impacto mediático, fue bien planificado por Shere Hite, que distribuyó 100.000 encuestas entre mujeres. Pero el problema es que sólo 3.019 se molestaron en contestar la encuesta y enviarla a la doctora Hite. No era obvio que de este pequeño grupo muy motivado por el tema pudieran sacarse grandes conclusiones para «todas las mujeres». 

LA FALACIA DE LA REGRESIÓN 

A finales del siglo XIX, sir Francis Galton hizo importantes contribuciones a temas de estadística que hoy son omnipresentes en todos los libros de texto. A él se debe la llamada regresión lineal, es decir, dadas dos variables X, Y, se dibujan en un plano los puntos (xi, yi) de los pares de valores y se busca una recta y = ax + b que «aproxime» bien a esta distribución de puntos. Lo curioso es que Galton falló en su primer ejemplo al considerar que «como padres excepcionalmente altos solían tener hijos de talla inferior a la suya, mientras que las personas muy bajas suelen tener hijos más altos que ellos», entonces era evidente que había una «regresión hacia la mediocridad». De esta falaz consideración (que no tenía en cuenta a la mayoría de la población) nació precisamente esta denominación de «regresión» que hoy es tan popular.

                                                                                                                         © 2025 JAVIER DE LUCAS