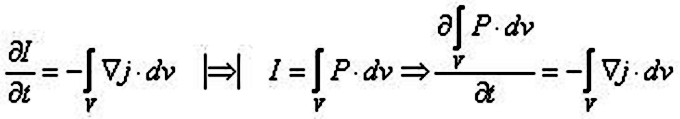LA ECUACION CUANTICA

La ecuación fundamental de la mecánica cuántica no relativista para la dinámica de una partícula, sin tener en cuenta el spin, es la ecuación de Schrödinger o ecuación de ondas:



Donde representan, respectivamente, la energía potencial, la constante de Plank y el operador laplaciano y ψ(r, t) es la llamada función de onda, que nos da toda la información sobre el estado físico de la partícula en un instante dado.
La conexión básica entre las propiedades de la función de onda, ψ(r, t) , y el comportamiento de la partícula asociada está expresada en términos de la densidad de probabilidad, P(r, t). Según un postulado enunciado por Max Born, la relación entre la densidad de probabilidad y la función de onda, es que la cantidad:



Es proporcional a la probabilidad de que al realizar una medida de las coordenadas de la partícula, los valores de estas pertenezcan al elemento diferencial de volumen dv.
Si además, ψ(r, t) cumple la llamada condición de normalización,



Entonces la expresión (2) “es” la probabilidad de que al realizar una medida de las coordenadas los valores de estas pertenezcan al sistema de volumen dv.
Se puede demostrar que si ψ(r, t) está normalizada para t = 0, permanece normalizada para cualquier otro instante de tiempo. Para llegar a ello, tomamos la ecuación de Schrödinger en cualquiera de sus dos formas:



Para una dimensión tendremos:



Derivando respecto al tiempo el integrando de (3), obtenemos:



Y sustituyendo en la integral



Para que esta función permanezca constante es necesario y suficiente que se tenga:



Para realizar la integración lo hacemos por partes. Poniendo:



Resulta:



Esta última integral también puede ser integrada por partes:



Resultando:



Con lo que, finalmente:



Pero esta última integral es justamente el primer término del primer miembro de (I); por lo tanto, podemos escribir:



Y esta última igualdad es cierta porque ψ(r, t) es una función de onda que cumple:

1) ψ(r, t) y su primera derivada son continuas en el espacio
2) ψ(r, t) tiende a cero para q tendiendo a + infinito o – infinito.

Cuando ψ(r, t) no es de cuadrado integrable, la función de onda no se puede normalizar. En tales casos no determina los valores absolutos de las probabilidades de las coordenadas, pero la razón de los valores de en dos puntos distintos del espacio, determinan la probabilidad relativa de las coordenadas.
Puede demostrarse que la densidad de probabilidad, P(r,t) = satisface la ecuación de continuidad:



Donde j recibe el nombre de densidad de corriente de probabilidad.
La demostración podemos hacerla teniendo en cuenta el ejemplo visto anteriormente, para el que habíamos obtenido (salvo límites finitos en la integral):



Esto, simbólicamente y pasando a tres coordenadas, se puede escribir:



Pero teniendo en cuenta las propiedades de los operadores diferenciales, resulta que la divergencia de la densidad de corriente de probabilidad vale:



Y esto es justamente el integrando cambiado de signo de (*) por lo que tendremos:



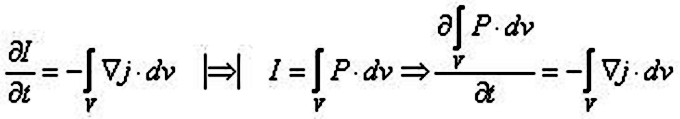
Y en forma diferencial:



Que es la expresión buscada.
El problema que se nos plantea es la obtención de soluciones de la ecuación (1) tales que para t = 0 nos den una función de onda, ψ(r, 0) determinada. Como la variable t no aparece explícitamente en dicha ecuación, utilizaremos el método d separación de variables para resolverla. Tenemos:



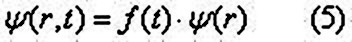
Y sustituyendo esta expresión en (1):



El primer miembro de esta ecuación depende únicamente de t, mientras que el segundo depende únicamente de r, por lo que podemos igualarlas a una constante, E:



De la primera de ellas obtenemos:



Puede demostrarse además que E es un número real que se puede identificar con el valor esperado de la energía total de la partícula para el estado ψ(r, t) .
Según lo visto, las soluciones de la ecuación (1) serán de la forma:



Siendo ψ(r) la solución de la ecuación de Schrödinger independiente del tiempo. Hemos de observar que para los estados determinados por las soluciones (8) el valor esperado de cualquier magnitud física que no depende explícitamente del tiempo, es constante. Por lo tanto, decimos que las funciones de onda tales como (8) representan estados estacionarios.

Las condiciones de regularidad que, por consideraciones físicas, debemos imponer a las soluciones ψ(r) de la ecuación de Schrödinger independiente del tiempo (6) dan lugar a que en muchas ocasiones, dichas soluciones dependen del parámetro E, no de forma continua, sino en valores aislados.

Los valores de E para los cuales existen soluciones de (6) compatibles con las condiciones de contorno impuestas, constituyen el llamado espectro de energía de la ecuación de Schrödinger. Este espectro puede estar constituido por valores aislados (niveles d energía discretos) o por intervalos continuos de valores.
Las funciones de onda de estados estacionarios son soluciones particulares de la ecuación de ondas. La solución general de (1) es de la forma:



Donde sumatorio implica integración si una parte o todo el espectro de energía es continuo. Cuando la ecuación de Schrödinger tiene más de una solución independiente para un mismo valor de E, la expresión anterior puede incluir el mismo valor de la energía más de una vez, y se dice que dicho nivel energético está degenerado.
Para que (9) sea la solución buscada es necesario que la función de onda de un estado inicial determinado puede descomponerse en la forma:



Cuando esta expresión es posible, decimos que el conjunto de soluciones estacionarias ψ_E(r) de la ecuación de Schrödinger es completo.

Las condiciones para dicha descomposición vienen impuestas por la forma de los potenciales V(r) que aparecen comúnmente en la ecuación de Schrödinger. Sin embargo, diremos que los potenciales V(r) que aparecen comúnmente en la ecuación permiten el desarrollo anterior para suficientes tipos de funciones, ψ(r, 0) .
Vamos a analizar ahora soluciones de la ecuación de Schrödinger para diferentes tipos de potenciales unidimensionales.

                                  VOLVER A FISICA                                                                                                                          © Javier De Lucas