

Prácticamente todo lo que sabemos sobre Física de partículas y fuerzas fundamentales gira en torno al concepto fundamental de simetría gauge. Las tres fuerzas fundamentales incluidas en el modelo estándar de la Física de partículas aparecen para restaurar localmente la simetrías gauge SU(3), SU(2) y U(1) lo que tiene como consecuencia la necesaria aparición de la fuerza fuerte, la fuerza débil y el electromagnetismo respectivamente. Sin embargo, ¿que pasa con la gravedad? ¿tiene algo que ver la simetría gauge con la gravedad? Como sabemos, aún no tenemos una teoría cuántica de la gravedad por lo que si existiese una conexión entre simetría gauge y gravedad quizás podríamos obtener una forma de cuantizar la gravedad. En este artículo veremos cómo esta relación nos conduce a una profunda conexión entre la geometría del espacio-tiempo y la geometría de esos espacios internos donde residen los campos gauge.
Relatividad especial y simetría
La relatividad especial implica que todos los observadores no inerciales deben medir las mismas magnitudes Físicas conservadas. Estas magnitudes conservadas son consecuencia de una simetría externa (espacio-temporal) fundamental: la simetría de Poincaré. Esta simetría incluye la invarianza ante traslaciones y la simetría de Lorentz. La importancia de este grupo de simetría queda plasmada en la definición de partícula fundamental: "una partícula fundamental se define como una representación irreductible del grupo de Poincaré". Esto básicamente significa que una partícula fundamental es una entidad que debe permanecer invariante ante traslaciones y ante transformaciones de Lorentz.
Relatividad general, geometría y simetrías gauge
La pregunta clave que queremos responder en este artículo es la siguiente: ¿Puede la gravedad ser formulada como una teoría gauge al igual que las otras tres fuerzas fundamentales? Una diferencia importante que debemos tener en cuenta es que las simetrías gauge del modelo estándar son simetrías internas mientras que las simetrías de la gravedad son simetrías del propio espacio-tiempo y por tanto son simetrías externas. ¿Podemos encontrar alguna relación entre estos espacios matemáticos internos y los espacios físicos externos del espacio-tiempo?
Al hacer una simetría gauge local aparece en el Lagrangiano del campo en cuestión un nuevo término. Para corregir este nuevo término y restaurar la simetría gauge debemos usar la derivada covariante, por ejemplo, de la siguiente forma:
![]()
En
relatividad general se usan los tensores para asegurar que los
sistemas de coordenadas permanecen válidos para cualquier
observador. Sin embargo, es sabido que en geometría diferencial las
derivadas parciales no transforman de forma tensorial y por tanto no
sirven para comparar dos sistemas de referencia diferentes:
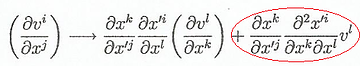
Si
comparamos la expresión anterior con la definición de tensor vemos
que tenemos un término extra (el término de la derecha). Para
conseguir que la transformación sea covariante (equivalente para
todos los sistemas de referencia) necesitaríamos usar una derivada
que cancelase este término extra, es decir, una derivada definida
como:
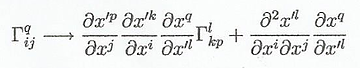
De
esta forma podríamos definir una derivada covariante
de la forma:
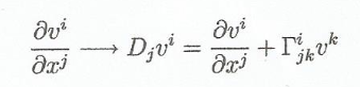
Y conseguir así cancelar el término extra que obtuvimos en la derivada parcial "usual".
Es fácil darse cuenta de que el proceso que acabamos de describir es muy similar al que seguimos en el artículo anterior para transformar una simetría gauge global en una simetría gauge local. De hecho, transformar una simetría global en local es similar a pasar de la relatividad especial a la relatividad general: la relatividad especial implica que los campos deben permanecer invariantes ante traslaciones y transformaciones de Lorentz.
Estas
transformaciones implican simetrías
espacio-temporales globales ya
que se producen con la misma magnitud en todos los puntos del
espacio-tiempo. Si hacemos estas simetrías locales hacemos que las
traslaciones cambien con diferente magnitud en función del
espacio-tiempo, es decir, ahora se permiten variaciones de la
posición (velocidades) en las traslaciones dependiendo del espacio o
el tiempo ¡exactamente lo que
cabría esperar en marcos de referencia acelerados! ¡Empezamos
a vislumbrar el vínculo entre simetrías gauge y gravedad!
El término final de la derivada covariante que vimos en la última expresión (el término corrector) está ligado a un término denominado conexión. La conexión juega un papel principal en relatividad general ya que describe la curvatura del espacio-tiempo. ¡Este es el vínculo que buscábamos entre gravedad y simetrías gauge! Ahora vemos una clara similitud entre las simetrías gauge y el principio de covarianza de la relatividad general: para que todos los observadores midan las mismas magnitudes invariantes de forma local tiene que aparecer un nuevo término que representa una nueva fuerza (la gravedad) y el efecto de este nuevo término es el de curvar el espacio-tiempo.
La teoría gauge de la gravedad
Si queremos obtener de forma rigurosa una teoría gauge de la gravedad la forma más obvia de proceder sería realizar el mismo proceso que hicimos con los campos gauge internos, es decir, tomar la simetría global de la relatividad y transformarla en una simetría local para ver si, al tratar restaurar la simetría, aparece un nuevo campo "gauge" que implique una nueva fuerza fundamental.
Este
proceso se ha realizado tomando como base el grupo fundamental de la
relatividad: el grupo de Poincaré P(1,3) que es el producto
semidirecto del grupo de traslaciones T(4) y el grupo de Lorentz
SO(1,3). Los resultados obtenidos de este proceso son impresionantes
aunque con un "giro" inesperado : los físicos no han
obtenido las ecuaciones de la relatividad general como esperaban sino
las ecuaciones de una teoría equivalente: La
teoría de Einstein-Cartan.
La teoría de Einstein-Cartan produce los mismos resultados que la relatividad general y puede considerarse una generalización de la teoría de Einstein para espacio-tiempos con torsión. Actualmente, con la tecnología presente no es posible diferenciar experimentalmente si vivimos en un Universo con torsión o sin torsión ya que sus efectos son muy pequeños. Considerando entonces una torsión nula la teoría de la relatividad general y la teoría de Einstein-Cartan son igualmente válidas. La conclusión de esto es de una importancia capital: Es posible obtener una teoría de la gravedad totalmente viable y operativa a partir de los principios de la simetría gauge.
Simetrías gauge y teoría de cuerdas
Aunque no están tan firmemente establecidas como la teoría de Einstein-Cartan existen otras teorías gauge de la gravedad aún más generales que esta. Una de ellas es la teoría gauge de Poincaré. La simetría de Poincaré puede "aumentarse" aún más incluyendo una simetría aún más general que intercambia bosones y leptones: La supersimetría. De esta forma "ascendemos" un poco más y obtenemos la teoría de la supergravedad.
La
supergravedad constituye un límite de baja energía de la teoría
más general y prometedora que tenemos para unificar las cuatro
fuerzas fundamentales: la teoría de supercuerdas.
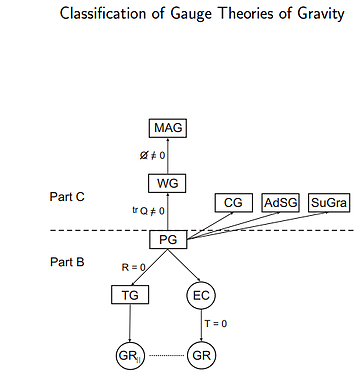
Teorías gauge de la gravedad: GR=Relatividad general EC=Teoría de Einstein Cartan TG= Translation Gauge Theory PG= Poincare Gauge Theory CG=Conformal Gauge Theory AdSG= Anti-deSitter Gauge Theory SuGRA= Supergravedad WG= Weyl(-Cartan) Gauge Theory MAG=Metric-Affine Gauge Theory. Las teorías representadas con un círculo (GR Y EC) son teorías verificadas y validadas experimentalmente, el resto son candidatos pendientes de validación.
Los físicos Kaluza en 1919 y Klein en 1926 consiguieron formular las ecuaciones de la relatividad general en un espacio-tiempo de 5 dimensiones y lograron algo extraordinario: la unificación de la relatividad general y el electromagnetismo. El hecho de aumentar el número de dimensiones espacio-temporales de 4 a 5 consigue incluir en las ecuaciones de movimiento el efecto de las simetrías gauge: la carga es el movimiento de una partícula neutra en la quinta dimensión mientras que los campos eléctricos surgen debido al movimiento de partículas en la nueva dimensión. Más aún: las transformaciones de coordenadas en la quinta dimensión equivalen a las transformaciones gauge del grupo U(1). Actualmente la teoría de Kaluza-Klein sigue siendo solo un marco teórico (aunque con extraordinarias consecuencias) pero sirve para ilustrar la intrincada relación entre simetrías internas y simetrías externas.
La teoría de (super)cuerdas es un marco teórico descrito en 10 dimensiones que constituye nuestro mejor candidato para unificar las cuatro fuerzas fundamentales de la naturaleza. Esta teoría incorpora de forma genérica las simetrías gauge ya que las branas (objetos extendidos multidimensionales) siempre incorporan de forma natural un campo gauge SU(N). Esta teoría utiliza simetrías gauge superiores a la del modelo estándar ya que se basa en grupos como el SO(32) o el E(8)xE(8) y constituye un marco geométrico unificador tanto de simetrías externas como de simetrías internas.
Este marco unificador no solo aspira a convertirse en una teoría cuántica de la gravedad sino a convertirse en una teoría de todas las fuerzas y campos fundamentales que existen: la denominada Teoría del Todo.
Conclusiones
Probablemente es uno de los aspectos más fundamentales y poderosos del Universo que habitamos: el concepto de simetría. El poder de este concepto es tal que es capaz de explicar todas las interacciones conocidas, todas las fuerzas de la naturaleza, las magnitudes Físicas, el porque de sus valores, el porque de su existencia. De hecho, en Física de partículas, sabemos que solo las magnitudes que son invariantes gauge pueden ser medidas empíricamente.
Pero aún hay más: las simetrías que vemos son solo las "cenizas" de simetrías mayores que existían cuando el Universo tenía muy alta energía. Es probable que siguiendo el "rastro" de la simetría podremos acercarnos hacía la "simetría fundamental" de la que se originó todo y explicar la propia naturaleza del espacio-tiempo y las fuerzas fundamentales. Parece existir un vínculo entre las simetrías externas espacio-temporales que todos vemos y reconocemos y las simetrías internas; este vínculo recuerda enormemente al intrincado vínculo entre Física y Matemáticas.
© 2020 Javier De Lucas