KAOS

A lo largo de muchos años, en el estudio que varias ciencias han hecho de diferentes fenómenos se han encontrado situaciones que no ha sido posible describir de manera satisfactoria. Por ejemplo, en el caso de la meteorología un problema muy importante es poder predecir el clima que prevalecerá no sólo al día siguiente, sino una semana, un mes, un año después. Sin embargo, a pesar de que esta ciencia se ha desarrollado bastante y mucha gente ha trabajado en ella durante más de un siglo, este tipo de predicciones no ha podido llevarse a cabo de manera efectiva.

En Física podemos mencionar el fenómeno de la turbulencia. Cuando un fluido se mueve a lo largo de un tubo, en ciertas condiciones el fluido lo hace de manera muy tranquila y regular; se dice que el flujo es laminar y sus propiedades sí han podido ser determinadas. Sin embargo, en otras circunstancias, el flujo se vuelve turbulento: empiezan a aparecer primero pequeños remolinos, después remolinos más y más grandes y el movimiento del fluido se vuelve muy irregular. Se dice que el flujo ha entrado en turbulencia. Este efecto no se había podido entender en más de cien años de estudio de la hidrodinámica.

En la economía no se han podido entender los motivos por los cuales en cierto momento el índice de la Bolsa de Valores empieza a subir y luego desciende. En muchas ocasiones parece ser un fenómeno del azar. Los casos anteriores ilustran algunos de los problemas que habían quedado sin solución. Sin embargo, con el advenimiento de la teoría del caos se han podido entender diferentes aspectos de estos fenómenos, antes incomprensibles.

Una cuestión muy importante, común a diferentes fenómenos, es la posibilidad de que se pueda hacer predicciones. Por ejemplo, si se sabe que hoy está lloviendo, se quisiera predecir si lloverá mañana o si lloverá pasado mañana. Es decir, una cuestión es la posibilidad de poder predecir lo que ocurrirá en el futuro si sabemos en qué situación nos encontramos ahora. En los últimos años se ha desarrollado una novedosa forma de abordar este tipo de situaciones. Resulta que muchos fenómenos completamente distintos, como la turbulencia, el clima, el índice de la bolsa, las señales electrónicas, ciertas reacciones químicas y otras más, tienen comportamientos que, vistos desde perspectivas apropiadas, son muy parecidos. Debido a este hecho, trataré un caso muy especial para ilustrar el fenómeno del así llamado caos.

Consideraremos un problema importante en la ecología, a saber, cómo evoluciona en el transcurso del tiempo una población determinada, por ejemplo de los insectos. Si conocemos el número de insectos este año, nos podemos preguntar ¿cuántos insectos habrá el año próximo, el siguiente, y así sucesivamente? Con el estudio que se haga se quisiera poder encontrar una regla que nos dijera que si este año hay, por ejemplo, en un determinado lugar 10 500 insectos, el próximo año habrá 12 750. Si se puede descubrir esta regla, entonces aplicándola de año en año se podrá conocer la población en cualquier año futuro.

En matemáticas una regla de este tipo se llama función. ¿De qué depende ésta? Pues debería hacerlo de las condiciones en que vive la población. No dará lo mismo si se trata de un lugar desértico o de una selva; si la población dispone de muchos alimentos o si más bien son escasos. Es decir; de alguna manera en la función tiene que aparecer esta información. Además, la población que vaya a haber el año siguiente dependerá de la población que existe en este año. Encontrar esta función se llama hacer o construir un modelo.

La función más sencilla es la siguiente. Se supondrá que la población crecerá el año siguiente en un porcentaje fijo de la población del año actual. Por ejemplo, si la población crece año con año 10%, se tiene la siguiente situación: supongamos que en el presente año hay 10 000 insectos; entonces el año próximo aumentará en 10% este número, así, habrá un aumento de:

y por tanto, el número de insectos que habrá el año próximo será igual al número que hay en el presente año (10 000) más el aumento que ocurrió (1000), o sea:

De esta manera se puede calcular el número de insectos del año que se quiera. Sin embargo, hacerlo a un plazo de 150 años, por ejemplo, sería muy engorroso. Pero puede abreviarse este procedimiento como sigue. Nos damos cuenta de que se puede encontrar la población del año siguiente (11000 en nuestro ejemplo) haciendo la siguiente operación:

Aquí, 10 000 es la población inicial. De la misma forma, la población en el segundo año (12 100) se puede obtener a partir de la población en el primer año (11 000) haciendo la siguiente multiplicación:

Vemos entonces que la población en cualquier año se encuentra multiplicando 1.1 por la población del año anterior. O equivalentemente, la población del año siguiente se puede encontrar multiplicando 1.1 por la población del año presente: Población del año próximo = 1.1 × Población del año presente. La población de un año cualquiera se introduce como dato para encontrar la población del año siguiente. Repitiendo o iterando esta operación tantas veces como se quiera, se encontrará la población de cualquier año futuro. La operación que acabamos de encontrar es la función a la que me referí arriba.

De lo que acabo de explicar nos damos cuenta de que si se conoce la función y la población inicial, entonces es posible determinar con precisión la población en cualquier año futuro. Se puede abreviar el procedimiento presentado de la manera siguiente: la letra x será la población en cierto año y la letra y la población del año siguiente. Entonces:

Para obtener y se multiplica 1.1 por x. El 1.1 proviene del hecho que se supuso que el crecimiento sería de 10% anual. Sin embargo, no siempre será así, podrá haber otras posibilidades. Si así fuera, el 1.1 se sustituirá por otro número. De manera general, este otro número se representará con la letra q. Así, la función se puede escribir:

Población del año próximo = q × Población del año presente El valor numérico que tenga el factor q que aparece en esta expresión dependerá de las condiciones en que ocurra el aumento de la población. En la forma en que se establece el modelo considerado, el valor de q varía de 0 a 4. Se puede representar la información contenida en esta expresión de manera gráfica. En una gráfica, en el eje horizontal (figura 17) se miden los valores de x y en el eje vertical los valores de y. La expresión (5) queda representada por una línea recta. Mientras mayor sea el valor de q, mayor será la inclinación de la recta. Debido a que la gráfica de la ecuación (5) es una recta se dice que la expresión (5) es lineal.

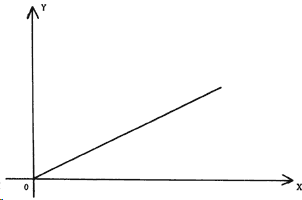
Figura 1. Gráfica del modelo que muestra la población de insectos del año próximo y) determinada por la población del año presente (x). En este momento la población crece sin cesar.

Una consecuencia de la aplicación de esta función es que, al transcurrir el tiempo, la población crecerá de manera indefinida; llegará un momento en que será tan grande que el número de individuos de la especie no cabría en el planeta. Es claro que un modelo como el que acabamos de presentar no puede describir de manera correcta las variaciones reales de una población. Si ésta crece mucho, llegará un momento en que los alimentos no alcancen para todos y, por tanto, la población empezará a descender. Este efecto debe considerarse, por lo que la función dada por la expresión (5) se deberá modificar para que tome en cuenta que una población puede crecer, pero hasta cierto punto; más allá deberá reducirse. Por otro lado, si la población es pequeña, entonces tendrá mucho alimento disponible y crecerá.

Lo anterior significa que la gráfica de la figura 17 deberá ser reemplazada por otra en la que para valores pequeños de x, o sea de la población, la curva suba, mientras que para valores muy grandes de x la curva disminuya. Esta gráfica se deberá ver como se muestra en la figura 18. Para que la curva disminuya, necesariamente tendrá un máximo; es decir, la curva deberá tener la forma de una campana invertida. El lector se dará cuenta de que esta curva ya no es una línea recta. Por tanto, a esta situación se le llama no lineal.

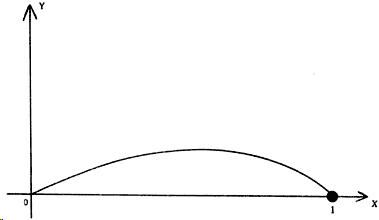
Figura 2. Modificación del modelo de la figura 1 para tomar en cuenta el hecho de que llega un momento en que la población no puede crecer indefinidamente.

y = población del año del año próximo; x = población del año del año presente. Esta expresión implica que, dado el valor de la población en el presente año (valor representado por x), se obtendrá el valor y de la población del año siguiente. Por conveniencia se han tomado x y y como la fracción entre los valores cero y uno, por tanto 0 ≤ q ≤ y. El valor cero representa la extinción de la población y el valor uno el máximo valor posible de la población.

Lo que nos está diciendo la ecuación (6) es que si se da x, para obtener el valor de y las operaciones que hay que hacer son:

Si ahora se usa como valor inicial de la población el valor que acabamos de encontrar, o sea 0.525, siguiendo el procedimiento se obtiene que la población al tercer año será 0.6234. Siguiendo esta iteración se encuentran sucesivamente los siguientes valores de la población en años sucesivos (se deja al lector verificar que estos valores efectivamente se obtienen):

Estos resultados nos indican que a partir de cierto momento la población llega a un valor que ya no cambia con el tiempo. En nuestro caso, la población llega al valor 0.6000. En el caso que acabamos de tratar, se empezó con la población inicial de x = 0.7 y se terminó con la de 0.6000. Si en lugar de haber empezado con 0.7 se hubiera empezado con el valor inicial de x = 0.25 (para el mismo valor de q de 2.5), siguiendo el mismo procedimiento iterativo se obtendrían los siguientes valores:

¡Se llega al mismo valor final de 0.6000! O sea, si se empieza con otra condición inicial se llega al mismo valor final. Así se comience con el valor que sea, para este caso de q = 2.5, siempre se llegará al mismo valor final de 0.6. Este resultado nos indica varias cosas acerca de la ecuación (6). En primer lugar, la población no crece indefinidamente por más iteraciones que se hagan. En segundo lugar, después de algunos años se alcanza un valor que NO depende de cuál haya sido el valor de la población inicial. Es decir, el valor 0.6 no depende de la condición inicial. Se logra así una población estacionaria: la misma año con año.

Si se vuelve a repetir este procedimiento pero para otro valor de q en la ecuación (6) se obtendrá otro valor final. Por ejemplo, si se usa para q el valor de 2.7, el valor final que se obtiene es 0.6296. Nótese que: para q 2.5 se obtiene como valor final 0.6. para q2.7 se obtiene como valor final 0.6296. A medida que q aumenta de valor, el valor final también aumenta su valor.

Vayamos ahora al otro extremo, el de un valor de q pequeño, por ejemplo 0.4. Si se empieza con una población de 0.3, entonces los valores de la población que se van obteniendo son los siguientes:

El valor final al que se llega es cero. ¡La población se extingue! De hecho, para los valores de q menores o iguales que 1, la población se extingue con el tiempo, sin importar cuál sea su valor inicial. Ahora nos vamos al extremo de valores grandes de q. Por ejemplo, usemos para q el valor de 3.3 y el inicial de la población de 0.6. Así se van obteniendo los siguientes valores:

Ahora no se obtiene un solo valor final que se vaya repitiendo año con año, sino que se va pasando del valor 0.8236 al de 0.4794 sucesivamente. Es decir, ahora la población en un año tendrá el valor de 0.4794 y al año siguiente el de 0.8236; el año siguiente se repetirá el valor de 0.4794 y luego, nuevamente el de 0.8236, y así sucesivamente. Esto significa que ahora se tienen dos valores finales posibles y que el valor de 0.4794 se alcanza no cada año sino cada dos años. Lo mismo ocurre con el otro valor de 0.8236. Es decir, el ciclo ahora dobló su valor de un año a dos; es decir, aparece ahora una periodicidad de 2 años. Nótese que los valores 0.8236 y 0.4794 no dependen del valor inicial que se escogió. Si en lugar de 0.6 se hubiera tomado otro valor, llegaríamos a los mismos valores finales (0.8236 y 0.4794); esto siempre y cuando se mantenga el mismo valor de q o sea, 3.3. Se dice que estamos en condiciones de periodo dos.

Para el valor de q = 3.5, con la condición inicial de 0.6, se obtienen, después de varias iteraciones, no dos valores finales sino cuatro, que son 0.3028, 0.8260, 0.5001 y 0.8750. Estos cuatro valores se van repitiendo, en el orden dado. Ahora esto corresponde al período 4. Si se sigue aumentando el valor de q, se obtienen ocho valores finales. Para q =3.55 por ejemplo, éstos son:

Para q =3.651, ahora los valores finales serán 16, que ya no escribiremos. Al seguir aumentando q se obtienen, sucesivamente, 32, 64, 128,… valores finales. Si ahora se escoge para q el valor de 3.6, resulta que por más iteraciones que se hagan no se llega a un valor final, en el sentido de que este valor (o valores) se repita como en los casos mencionados arriba. Ahora se encuentra una sucesión de números que no se repiten y que tienen toda la apariencia de una sucesión escogida al azar. Si se cambia la condición inicial, pero se mantiene el valor de q 3.6, se obtiene otra sucesión con números distintos de los anteriores y que tampoco adquiere valores finales que se repiten constantemente.

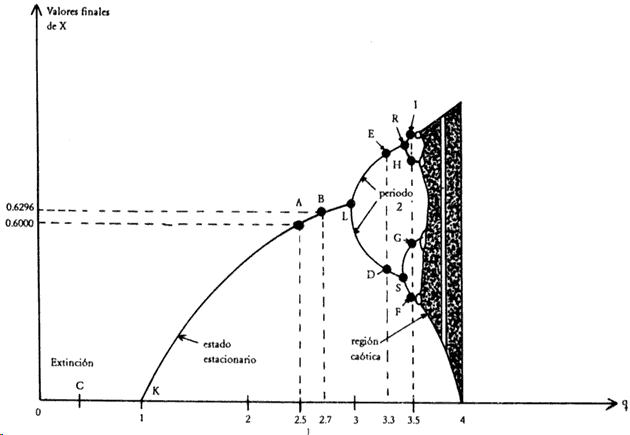
Figura 3. Gráfica de los valores finales que se obtienen con referencia a la población como función del parámetro q y que muestra dos tipos de regímenes: el periódico (estable) y el caótico.

Estos resultados pueden observarse haciendo la siguiente gráfica (figura 3). En el eje horizontal mediremos los valores de q; en el eje vertical se medirá(n) el(los) valor(es) final(es) que se obtenga(n) para el correspondiente valor de q. Así:

• para q = 3.3, cuyos valores finales = 0.8236 y 0.4794 le corresponden los puntos D y E;

• para q = 3.5, cuyos valores finales no los escribiremos, le corresponden los puntos F, G, H, I, etcétera.

Los valores de q para los cuales no se obtienen valores finales, se marcarán en la gráfica con una línea completa, ya que todos los valores son posibles. De la gráfica se puede observar lo siguiente, a medida que va aumentando el valor de q: Para q menor o igual que 1, los valores son nulos; hay extinción de la población. Para q entre 1 y 3 , solamente hay un solo valor final, el del estado estacionario, que va aumentando a medida que q aumenta. En este intervalo la gráfica es la línea curva KL.

Al seguir aumentando q, en L empieza a aparecer una bifurcación que da dos valores finales. Así q entre 3 y 3.45 tiene dos valores finales; estamos en la región del periodo 2. La gráfica en este intervalo consiste en dos líneas curvas, la LR y la LS. Si q sigue aumentando, para el valor de 3.45 (aproximadamente) aparecen otras dos bifurcaciones y ahora se tendrán cuatro valores finales. De hecho entre 3.45 y 3.54 estaremos en la región del periodo 4 y la gráfica muestra cuatro líneas curvas, que ya no nombraremos.

Al seguir aumentando q, aparecen nuevas bifurcaciones y nuevas líneas curvas hasta que, finalmente, cuando q adquiere el valor de 3.5699 ya no hay valores finales fijos y se tiene una región con manchas que se llama caótica. En esta región y adquiere cualquier valor. Como se puede apreciar en la figura, dentro de la región caótica aparecen regiones que sí tienen valores fijos. Éstas son las regiones blancas de la figura. En efecto, para q alrededor del valor 3.84 aparece una región con valores finales bien determinados. Ahora se obtienen tres valores: 0.1494, 0.4879 y 0.9594. Al seguir aumentando q hay una bifurcación y por ejemplo, para q 3.846, ahora hay seis valores finales. Al seguir aumentando q siguen las bifurcaciones, hasta que se llega a una nueva región caótica. Podemos entonces afirmar que al ir aumentando q, se pasa por los siguientes regímenes: extinción → un solo valor final → periódicos con periodicidades de 2, 4, 8, 16,… → caótico → periódicos con periodicidades de 3, 6,…→caótico, …

Estos resultados se obtuvieron con el estudio de la función dada por la ecuación (6). Sin embargo, hay muchas otras funciones, distintas de ésta, pero cuyas gráficas tienen la misma forma cualitativa mostrada en la figura 3. Resulta que para todas estas funciones distintas el comportamiento de los valores finales es el mismo que expliqué antes. Este comportamiento es característico de las funciones no lineales.

Regresemos al caos de la población de insectos. Vimos que si el valor del parámetro q de la ecuación (6) es suficientemente pequeño, entonces, sea cual sea el valor inicial de la población, es decir, el valor inicial de x, después de cierto número de iteraciones se llega a un valor final que ya no cambia al seguir iterando. Recordando que cada iteración nos da el valor de la población un año después, concluimos que si q es suficientemente pequeño, después de cierto tiempo se llega a una población final que ya no varía al transcurrir el tiempo.

Si q aumenta, ocurre que después de ciertas iteraciones la cantidad x adquiere dos valores. En una iteración adquiere el primero, y en la siguiente, el segundo, y estos dos valores se van alternando. Esto significa que después de cierto tiempo, en un año la población tiene un valor y al siguiente el segundo valor. En el tercero la población vuelve a tener el primer valor, en el cuarto el segundo valor, y así sucesivamente. Por lo tanto, el primer valor final lo adquiere la población cada dos años; lo mismo ocurre con el segundo valor, la población lo va adquiriendo cada dos años. Éste era el régimen que se llama de periodicidad dos.

Al seguir aumentando el valor de q se llega a un régimen final en el que hay cuatro posibles valores finales de la población, que se van alternando. Por tanto, cada uno de estos valores se va adquiriendo cada cuatro años. Estamos en el caso de la periodicidad cuatro. Podemos así continuar, hasta que se llegue al régimen caótico, en que cada año la población va adquiriendo cierto valor que ya no se repite. Ahora bien, lo anterior significa que, antes de entrar en el régimen caótico, el periodo va aumentando de 1 a 2 años, a 4 años, a 8 años, etc., a medida que el valor de q va aumentando. Llega cierto momento en que ya no se puede hablar de periodo, se ha entrado en el régimen caótico.

Otra forma de presentar estos resultados es en términos de la frecuencia y no del periodo. Estas dos cantidades están íntimamente relacionadas. El periodo es el tiempo que tarda algún fenómeno en volverse a repetir, por ejemplo, el tiempo en que tarda la Tierra en dar una vuelta alrededor de su eje es el periodo de su rotación. Como sabemos este periodo es de 24 horas. Es claro que para poder hablar de periodo el fenómeno debe ser repetitivo, esto es, periódico. La frecuencia de un fenómeno periódico es el número de veces que se repite en un segundo, en un minuto o en otra unidad de tiempo. Si un tocadiscos da 33 vueltas por minuto, esto significa que su frecuencia es de 33 revoluciones por minuto, abreviado 33 rpm.

Un ejemplo de fenómeno repetitivo es cuando un cuerpo se mueve alrededor de un círculo. Supongamos que el cuerpo tarda 5 segundos en dar una vuelta; su periodo es de 5 segundos. Por lo tanto, en un segundo el cuerpo habrá dado (1/5) de vuelta; su frecuencia es (1/5) = 0.2. De este ejemplo vemos que si el periodo tiene cierto valor, llamémosle T, entonces su frecuencia es igual a (1/T). La frecuencia es igual al inverso del periodo. Regresando al caso de la población que estudiamos antes, llegamos a la conclusión de que al ir aumentando el valor de q el periodo aumenta a 2, luego a 4, luego a 8, y así sucesivamente, hasta llegar al régimen caótico. Expresando esto en términos de frecuencia, vemos que si para un valor de q solamente hay un periodo esto equivale a un valor de la frecuencia.

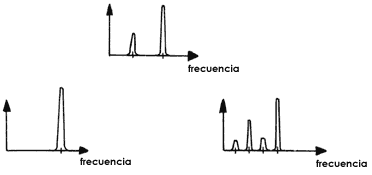
Figura 4 Gráficas que muestran las frecuencias características que gobiernan el fenómeno para valores recientes de q. A medida que q crece, aumenta el número de frecuencias.

Al aumentar el valor de q, el periodo aumenta al doble y por tanto, la frecuencia disminuye entonces a la mitad. Al seguir aumentando el valor de q, el periodo aumenta cuatro veces, por lo que la frecuencia disminuye cuatro veces. Al continuar aumentando el valor de q, el periodo aumenta ocho veces, por lo que la frecuencia disminuye ocho veces, etcétera.

En consecuencia, si para cada valor de q se hiciera una gráfica de la frecuencia que corresponde al fenómeno, se encontraría la sucesión de gráficas de la figura 4. Cada gráfica de esta sucesión corresponde a un valor de q. Vemos entonces que los picos de las gráficas, a medida que q aumenta, van apareciendo a la mitad del valor de la frecuencia anterior. Cuando se llega al régimen caótico, entonces ya no hay ningún pico, ya que no hay periodo, y por tanto, no hay ninguna frecuencia característica.

Una forma de obtener resultados experimentales, como en el caso de la turbulencia, es por medio de análisis de frecuencias del fenómeno en cuestión. Éste es el motivo por el cual introduje la explicación en términos de esta cantidad.