LA TEORIA ASOMBROSA

LA TEORIA ASOMBROSA

LA MAGICA, MISTERIOSA Y ASOMBROSA TEORIA M

En 1985 la teoría de cuerdas —ahora llamada teoría de supercuerdas— tenía cinco versiones distintas. Diferían en varios aspectos. Dos de ellas tenían cuerdas abiertas (cuerdas con dos extremos) tanto como cuerdas cerradas, y tres no lo hacían. Los nombres de la cinco no son particularmente ilustrativos, pero aquí el super se refiere al hecho de que todas estas teorías tienen gemelos fermión-bosón y eran, por consiguiente, supersimétricas. Las dos con cuerdas abiertas se llaman teorías de cuerdas tipo Ia y Ib. Las tres restantes, con sólo cuerdas cerradas, se conocen como teorías de cuerdas tipo IIa, tipo IIb, y heterótica. Las diferencias son demasiado técnicas para describir sin aburrir al lector. Pero una cosa que tienen en común es mucho más interesante que cualquiera de las diferencias: aunque algunas tienen cuerdas abiertas y otras no las tienen, las cinco versiones tienen cuerdas cerradas.

Para apreciar por qué esto es tan interesante tenemos que entender una característica muy desagradable de todas las teorías anteriores. En las teorías ordinarias —teorías tales como la electrodinámica cuántica o el modelo estándar— la gravedad es un «añadido» opcional. Se puede ignorar la gravedad o añadirla al grupo. La receta es simple: tomamos el modelo estándar y añadimos una partícula más, el gravitón. Sea el gravitón sin masa. Añadamos también algunos nuevos vértices: cualquier partícula puede emitir un gravitón. Ya está. Pero eso no funciona muy bien. Las matemáticas son intrincadas y sutiles, pero a la postre los nuevos diagramas de Feynman que incluyen gravitones dan al traste con los primeros cálculos. Todo sale infinito. No hay manera de dar sentido a la teoría.

En un aspecto creo que es bueno que el procedimiento simple fallara. No contiene ningún indicio de una explicación de las propiedades de las partículas, ninguna explicación de por qué el modelo estándar es especial y no explica nada sobre el ajuste fino de la constante cosmológica o la masa de Higgs. Francamente, si funcionase sería muy decepcionante. Pero las cinco teorías de cuerdas son muy claras en este punto: simplemente no pueden formularse sin gravedad. La gravedad no es un ingrediente arbitrario: es un producto inevitable. Para ser consistente la teoría de cuerdas debe incluir al gravitón y las fuerzas que él medía por intercambio. La razón es simple. El gravitón es una cuerda cerrada, la más ligera. Las cuerdas abiertas son opcionales, pero las cuerdas cerradas están siempre allí. Supongamos que tratamos de crear una teoría con sólo cuerdas abiertas. Si tuviéramos éxito tendríamos una teoría de cuerdas sin gravedad. Pero siempre fracasamos. Los dos extremos de una cuerda abierta siempre pueden encontrarse y unirse para formar una cuerda cerrada. Las teorías ordinarias sólo son consistentes si la gravedad queda fuera. La teoría de cuerdas sólo es consistente si incluye la gravedad. Ese hecho, más que cualquier otro, es lo que da confianza a los teóricos de cuerdas en que están en el camino correcto.

Las cuatro teorías etiquetadas tipos I y II fueron descubiertas inicialmente en los años setenta. Cada una de ellas tenía defectos fatales, no en su consistencia matemática interna sino en la comparación detallada con hechos experimentales sobre las partículas. Cada una describía un mundo posible. Sencillamente no describían nuestro mundo. Por ello se produjo una enorme excitación cuando se descubrió la quinta versión en Princeton en 1985. La teoría de cuerdas heterótica parecía ser el sueño del teórico de cuerdas. Se parecía lo suficiente al mundo real como para ser quizá la real.

Se anunció un éxito inminente. Incluso entonces había razones para recelar de las afirmaciones fuertes. Por una parte, seguía estando el problema de demasiadas dimensiones: nueve de espacio y una de tiempo. Pero los teóricos ya sabían lo que hacer con las seis dimensiones extra: «¡Compactifiquemos!», decían. Pero hay millones de elecciones posibles entre los espacios de Calabi Yau. Además, cada una de ellas da una teoría consistente. Peor aún, una vez que se escogía una variedad de Calabi-Yau había centenares de módulos (campos escalares) asociados con su forma y tamaño. También éstos tenían que ser fijados a mano. Además, todas las teorías conocidas eran supersimétricas: en cada caso las partículas se daban en pares exactamente ajustados, lo que sabemos que no encaja en nuestra realidad.

De todas formas, los teóricos de cuerdas estaban tan cegados por el mito de la unicidad que durante los años ochenta y principios de los noventa siguieron afirmando que había sólo cinco teorías de cuerdas. En su imaginación el paisaje era muy exiguo: sólo tenía cinco puntos. Por supuesto esto era absurdo, puesto que cada compactificación viene con muchos módulos que podrían variarse; pero a pesar de ello, los físicos se agarraban a la ficción de que sólo había cinco teorías para revisar. Incluso si sólo había cinco posibilidades, ¿qué principio seleccionaba, entre ellas, la que describe el mundo real? Ninguna idea afloraba. Pero en 1995 llegó un avance transcendental, no para descubrir la versión correcta que describe el mundo, sino para entender las relaciones entre las diversas versiones.

UNIVERSIDAD DE CALIFORNIA, 1965

Todos los años, a finales de primavera o comienzos del verano, los físicos teóricos de cuerdas de todo el mundo se reúnen para su congreso anual. Estadounidenses, europeos, japoneses, coreanos, indios, pakistaníes, israelíes, latinoamericanos, chinos, musulmanes, judíos, cristianos, hindúes; creyentes y ateos: todos se reunen durante una semana para oír las últimas ideas de los demás. Casi todos los cuatrocientos o quinientos participantes se conocen. Los veteranos son en general viejos amigos.Cuando se encuentran hacen lo que los físicos hacen siempre: dar y escuchar conferencias sobre los últimos temas calientes. banquete. El año 1995 fue memorable. La razón fue un suceso de importancia transcendental para las personas ahí reunidas: Ed Witten dio una conferencia en la que expuso avances espectaculares que orientaban el campo en direcciones totalmente nuevas.

Ed Witten, no sólo un gran físico-matemático sino también una figura destacada entre los matemáticos puros, venía siendo desde hacía tiempo la fuerza impulsora tras el desarrollo matemático de la teoría de cuerdas. Él es profesor (algunos dirían “el profesor”) y luz guía en el intelectualmente abarrotado Instituto para Estudios Avanzados. Más que cualquier otro, Witten ha impulsado decididamente los avances en el campo.

En 1995 se estaba haciendo evidente que el vacío descrito por la teoría de cuerdas estaba lejos de ser único. Había muchas versiones de la teoría, cada una de las cuales llevaba a leyes de la física diferentes. Esto no se veía como algo bueno, sino más bien como un inconveniente. Después de todo, diez años antes los teóricos de cuerdas de Princeton habían prometido no sólo que la teoría era casi única sino también que estaban a punto de encontrar la verdadera versión que describe a la Naturaleza. El objetivo primario de Witten había sido demostrar que todas las versiones salvo una eran matemáticamente inconsistentes. Pero en su lugar, él encontró un Paisaje, o más exactamente la porción del Paisaje a altitud cero, es decir, la parte supersimétrica del paisaje. Esto es lo que sucedió.

Imaginemos que los físicos hubieran descubierto dos teorías de electrones y fotones: la electrodinámica cuántica usual pero también una segunda teoría. En la segunda teoría, los electrones y los positrones, en lugar de moverse libremente a través del espacio tridimensional, podían moverse solamente en una dirección, digamos la dirección x. Sencillamente eran incapaces de moverse en cualquier otra dirección. Los fotones, por el contrario, se movían a la manera usual. La segunda teoría era un incordio. Hasta donde los físicos podían decir era matemáticamente tan consistente como la electrodinámica cuántica que gobernaba el mundo real de átomos y fotones, pero no tenía sitio en su visión del mundo real. ¿Cómo podía haber dos teorías, igualmente consistentes, sin ninguna forma de explicar por qué una debería ser descartada mientras que la otra describe la Naturaleza? Confiaban y rezaban para que alguien descubriera un fallo, una contradicción matemática, que eliminase la teoría indeseada y les diese razón para creer que el mundo es como es porque ningún otro mundo es posible.

Entonces, mientras intentaban demostrar que la segunda teoría era inconsistente, dieron con unos hechos interesantes. No sólo no encontraron ninguna inconsistencia sino que también empezaron a entender que las dos teorías eran parte de la misma teoría. Se dieron cuenta de que la segunda versión era meramente una versión límite de la teoría usual en una región del espacio con un campo magnético enormemente intenso: una máquina super RMI. Como le dirá cualquier físico, un campo magnético muy fuerte obligará a las partículas cargadas a moverse en una sola dirección: siguiendo las líneas de fuerza del campo magnético. Pero el movimiento de una partícula no cargada, como el fotón, no se ve afectado por el campo. En otras palabras, sólo hay una teoría, un conjunto de ecuaciones, pero dos soluciones. Aún mejor, variando el campo magnético de forma continua se interpola toda una familia de teorías entre ambos extremos. Los físicos ficticios habían descubierto un paisaje continuo y se disponían a explorarlo. Por supuesto, aún no tenían ninguna idea de qué mecanismo podría escoger entre el continuo de soluciones, por qué el mundo de la realidad no tiene ningún campo magnético de fondo. Esperaban explicarlo más tarde.

Ésta es exactamente la situación en que dejó Witten después de su charla de 1995 en Los Ángeles. Él había descubierto que las cinco versiones de la teoría de cuerdas eran en realidad soluciones de una única teoría: no muchas teorías, sino muchas soluciones. De hecho, todas pertenecían a una familia que incluye un miembro más, una teoría que Witten llamó teoría M. Además, cada una de las seis teorías corresponde a un valor extremo de los moduli: algún lejano rincón límite del paisaje. Como en el ejemplo del campo magnético, los módulos pueden variarse de forma continua de modo que una teoría se transforme en las otras. «Una teoría, muchas soluciones»: ése se convirtió en el eslogan guía. Las líneas de fuerza pueden verse fácilmente colocando un imán bajo una hoja de papel y esparciendo limaduras de hierro sobre la hoja. Las limaduras se alinean a lo largo de las líneas de campo y forman filamentos.

Hay muchas conjeturas sobre lo que representa la M. He aquí algunas de las posibilidades: madre, milagro, membrana, magia, misterio y maestra. Más adelante se añadió matriz. Nadie parece saber con certeza lo que Witten tenía en mente cuando acuñó el término teoría M. A diferencia de las cinco teorías previamente conocidas, la nueva pariente no es una teoría con nueve dimensiones de espacio y una de tiempo. En su lugar es una teoría con diez dimensiones de espacio y una de tiempo. Y lo que es incluso más alarmante, la teoría M no es una teoría de cuerdas: los objetos básicos de la teoría M son membranas, hojas de energía bidimensionales que se parecen a hojas elásticas en lugar de bandas elásticas unidimensionales.

La buena noticia era que la teoría M parecía ofrecer un marco unificador en el que aparecen las diversas teorías de cuerdas cuando una o más de las diez dimensiones de espacio se enrollan por compactificación. Éste fue un avance real que mantenía la promesa de una base unificadora para la teoría de cuerdas. Pero también había un lado negativo. No se sabía casi nada de la mezcla de la relatividad general oncedimensional con la mecánica cuántica. Las matemáticas de las membranas son terriblemente complicadas, mucho más que las de las cuerdas. La teoría M era tan oscura y misteriosa como cualquier teoría cuántica de la gravedad que hubiera existido antes de que la teoría de cuerdas hiciera su aparición. Parecía como si se hubiera dado un paso adelante y dos pasos atrás.

Eso no duró mucho tiempo. En la siguiente reunión de cuerdas, en el verano de 1996, cuatro físicos informaron que habían descubierto el secreto de la teoría M. Habían encontrado los objetos subyacentes en la teoría, y las ecuaciones que los gobernaban eran increíblemente simples. Tom Banks, Willy Fischler, Steve Shenker y Leonard Susskind descubrieron que las entidades fundamentales de la teoría M no eran membranas sino objetos más simples, «partones» básicos de un nuevo tipo. Similares en algunos aspectos a los viejos partones de Feynman, estos nuevos constituyentes tenían una sorprendente capacidad para ensamblarse y formar todo tipo de objetos. El propio gravitón, en un tiempo considerado la partícula más fundamental, era un compuesto de muchos partones. Ensamblaron los mismos partones en una pauta diferente y emergían membranas. En otra pauta formaban un agujero negro. Las ecuaciones detalladas de la teoría eran mucho más sencillas que las ecuaciones de la teoría de cuerdas, incluso más sencillas que las ecuaciones de la relatividad general.

La nueva teoría se llama teoría matriz o a veces teoría M(atriz) para resaltar su conexión con la teoría M. Witten no fue el primero en especular sobre una conexión entre una teoría oncedimensional y la teoría de cuerdas. Durante años varios físicos habían tratado de llamar la atención hacia una teoría oncedimensional con membranas. Mike Duff en Texas A&M (ahora en el Imperial College de Londres) había tenido muchas de las ideas años antes, pero los teóricos de cuerdas no las creían. Las membranas eran demasiado complicadas, y las matemáticas demasiado mal entendidas, para que la idea seminal de Duff fuera tomada en serio. Pero tratándose de Witten, los teóricos de cuerdas se adhirieron a la teoría M y nunca la dejaron.

¿Qué hay en la teoría M que captó de esa forma la imaginación de los físicos teóricos? No es una teoría de cuerdas. Ningún filamento de energía unidimensional habita este mundo de once dimensiones espacio-temporales. De modo que ¿por qué, de repente, los teóricos de cuerdas se interesaron en hojas de energía bidimensionales, membranas, como son llamadas? Las respuestas a estos enigmas residen en los sutiles misterios de la compactificación.

Imaginemos un cilindro infinito. Empezando con una hoja de papel infinito, recortamos primero una franja infinita de algunos centímetros de anchura. Pensemos en los dos bordes como si fueran el techo y suelo de una habitación bidimensional. La habitación es extraordinariamente grande. Se prolonga indefinidamente en la dirección x, pero en la dirección y está acotada por encima y por debajo por el techo y el suelo. En el paso siguiente el techo se une con el suelo para hacer un cilindro.

Imaginemos ahora una partícula que se mueve por la habitación infinita. En algún momento puede llegar al techo. ¿Qué sucede a continuación? Si la franja estuviera enrollada en un cilindro no habría problema: la partícula seguiría su curso, atravesando el techo y reapareciendo en el suelo. De hecho no necesitamos realmente doblar el papel para hacer un cilindro; basta saber que cada punto en el techo está emparejado con un único punto en el suelo de modo que cuando la partícula cruza un borde salta de repente al otro. Podemos enrollar el papel o dejarlo plano: sólo necesitamos seguir la regla por la que cada punto del techo se identifica con el punto del suelo que tiene por debajo en vertical.

Ahora avancemos un poco más: nuestra habitación es ahora tridimensional como una habitación real, excepto que es infinita, esta vez en la dirección x y en la dirección z. Pero la dirección y, la dirección vertical, está acotada por encima y por debajo por el techo y el suelo. Como antes, cuando una partícula atraviesa el techo reaparece al instante en el punto correspondiente del suelo. El espacio tridimensional se ha compactificado a dos dimensiones. Si la altura de la habitación —en otras palabras, la distancia alrededor de la dirección y— se contrajera a un tamaño microscópico, el espacio sería prácticamente bidimensional.

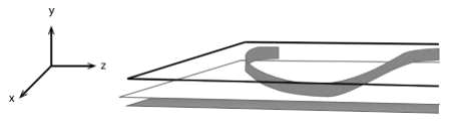
Como he dicho, la teoría M no tiene cuerdas sino sólo membranas. Así que ¿cuál es su relación con la teoría de cuerdas? Imaginemos una cinta, cuya anchura es exactamente la altura de la habitación, con su anchura extendida del suelo al techo. La longitud de la cinta recorre la habitación siguiendo una curva inscrita en el suelo. La única regla es que el borde superior de la cinta debe estar exactamente sobre el borde inferior. De hecho, la cinta no tiene más bordes que los que tenía el cilindro de papel. Pero es más fácil visualizar una larga cinta serpenteando a lo largo de la habitación infinita con sus bordes siguiendo el techo y el suelo.

Ahora usted debe tener una buena idea de cómo la cinta, en sí misma una membrana bidimensional, imita a una cuerda unidimensional. Si la dirección compacta fuera tan pequeña que no pudiera verse sin un microscopio, la cinta sería una cuerda para cualquier fin práctico. Si la cinta se cerrara sobre sí misma sería indistinguible de una cuerda cerrada: una cuerda tipo IIa, para ser precisos. Ésta es la conexión entre la teoría M y la teoría de cuerdas. Las cuerdas son en realidad cintas muy estrechas o membranas que se parecen cada vez más a cuerdas finas a medida que se contrae la distancia en la dirección y. Eso no es tan difícil.

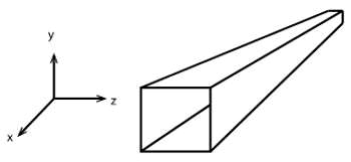
Pero las cosas pueden ser más extrañas. Demos ahora otro paso y compactifiquemos dos dimensiones: llamémoslas z e y. Para visualizar esto, imaginemos la habitación infinita reemplazada por un corredor infinito. Tenemos paredes a la izquierda y derecha, y un techo y un suelo por encima y por debajo. Pero si miramos a lo largo del corredor podemos ver indefinidamente en una u otra dirección. Una vez más, si un objeto llega al techo reaparece en el suelo. Pero ¿qué pasa si se aproxima a una de las paredes que acotan la dirección z? Usted ya sabe probablemente la respuesta: aparece en la pared opuesta, directamente enfrente del lugar donde tocó a la primera pared.

Exactamente el mismo truco puede hacerse en el espacio diez-dimensional de la teoría M, sólo que esta vez, el «corredor» se extiende indefinidamente en ocho de las diez direcciones espaciales. Como se podría esperar, cuando la altura y la anchura del corredor se hacen muy pequeñas el observador a gran escala piensa que está viviendo en un mundo de ocho dimensiones (más una de tiempo).

Ahora viene una consecuencia chocante y extraña de la teoría de cuerdas. Si la anchura y la altura del corredor se hacen más pequeñas que un cierto tamaño, una nueva dimensión sale de ninguna parte. Esta nueva dirección del espacio no es ninguna de las direcciones con las que empezamos. Sabemos de ella sólo a través de las matemáticas indirectas de la teoría de cuerdas. Cuanto más pequeñas hacemos las direcciones compactas originales, más grande se hace la dirección compacta recién creada. Finalmente, cuando el corredor se contrae hasta altura y anchura nulas, la nueva dirección se hace infinitamente grande. Sorprendentemente, al contraer dos de las dimensiones espaciales encontramos nueve, y no ocho, grandes direcciones restantes. Este hecho peculiar —que, «diez menos dos igual a nueve»— es una de las más extrañas consecuencias de la teoría de cuerdas. La geometría del espacio no es siempre la que Euclides o incluso Einstein pensaban. Evidentemente a las distancias más pequeñas el espacio es diferente de cualquier cosa que los físicos o los matemáticos imaginaron en sus peores sueños.

Quizá ahora esté usted ligeramente confundido sobre la diferencia exacta entre la teoría de cuerdas y la teoría M. Los teóricos de cuerdas también están confundidos sobre la terminología. Por ejemplo, ¿es la teoría once-dimensional, que contiene membranas pero no cuerdas, parte de la teoría de cuerdas? ¿Sigue siendo teoría M la versión compactificada de la teoría M cuando se transforma en teoría de cuerdas? Me temo que el campo ha sido bastante impreciso sobre estas cuestiones. Mi propia terminología consiste en llamar teoría de cuerdas a todo lo que salió de la teoría de cuerdas original. Eso incluye a todo lo que ahora se llama teoría M. Yo utilizo el término teoría M cuando quiero resaltar las características oncedimensionales de la teoría.

D-BRANAS

La teoría M tenía un serio problema: necesitaba nuevos objetos, objetos que la teoría de cuerdas no había predicho con anterioridad. La teoría tendría que hacer algo parecido a esto: cada una de las teorías de cuerdas debe contener objetos previamente insospechados ocultos profundamente en sus matemáticas. Las cuerdas fundamentales de una versión no eran los mismos objetos que las cuerdas fundamentales en otra versión. Pero cuando los módulos variaban —cuando uno se movía a lo largo del paisaje— los nuevos objetos de la versión A se metamorfoseaban en los viejos objetos de la versión B. Un ejemplo es cómo las membranas de la teoría M se metamorfosean en las cuerdas de la teoría tipo IIa. Las ideas de Witten eran atractivas —incluso convincentes— pero la naturaleza de los nuevos objetos y su lugar matemático en la teoría eran un completo misterio.

Mejor dicho, lo eran hasta que Joe Polchinski descubrió sus branas. Incluso antes de que Witten introdujera su teoría M, Polchinski había estado experimentando con una idea nueva en teoría de cuerdas. Un poco como juego matemático, él postuló que podría haber lugares en el espacio donde podrían terminar las cuerdas. Imaginemos a un niño que mantiene el extremo de una comba y la agita para hacer ondas. Las ondas viajan hasta el extremo lejano de la comba, pero lo que sucede a continuación depende de si el extremo lejano esta libre para moverse o está anclado a algo. Antes de Polchinski, las cuerdas abiertas siempre tenían extremos libres —la opción blanda— pero la nueva idea de Joe era que podía haber anclas en el espacio que impedían moverse a los extremos de la cuerda. El ancla podía ser un punto simple en el espacio: sería más o menos como una mano que impide férreamente el movimiento del extremo.

Pero hay otras posibilidades. Supongamos que el final de la cuerda estuviera atado a un anillo que puede deslizar arriba y abajo por un eje. El extremo estaría parcialmente fijo pero parcialmente libre para moverse. Aunque atado al eje, el extremo estaría libre para deslizar a lo largo de una línea: el propio eje. Lo que pueden hacer las combas unidas a ejes, lo pueden hacer las cuerdas, o así razonó Polchinski. ¿Por qué no tener líneas especiales en el espacio a las que podrían estar atados los extremos de las cuerdas? Como en el caso de la comba y el eje, el extremo de la cuerda estaría libre para deslizar a lo largo de la línea. La línea podría incluso estar curvada. Pero puntos y líneas no agotan las posibilidades. El extremo de la cuerda podría estar unido a una superficie, una especie de membrana. Libre para deslizar en cualquier dirección a lo largo de la superficie, el extremo de la cuerda no podría escapar de la membrana.

Estos puntos, líneas y superficies donde podrían terminar las cuerdas necesitaban un nombre. Joe las llamó Dirichlet-branas o simplemente D-branas. Peter Dirichlet fue un matemático alemán del siglo XIX que no tuvo nada que ver con la teoría de cuerdas. Pero ciento cincuenta años antes había estudiado las matemáticas de las ondas y cómo se reflejaban en objetos fijos. Con todo derecho los nuevos objetos deberían llamarse Polchinski-branas, pero el término P-branas ya era usado por los teóricos de cuerdas para otro tipo de objeto.

Solo poco después de la conferencia de Witten de 1995 las D-branas irrumpieron en la conciencia de los físicos teóricos. ¿Cuál es la relación con la conferencia de Witten? Unos meses después, en noviembre, Joe Polchinski escribió un artículo que ha tenido tremendas repercusiones en todas las áreas de la física teórica. Los nuevos objetos que necesitaba Witten eran exactamente las D-branas de Joe Polchinski. Armados con las D-branas, los físicos podían ahora completar el proyecto de Witten de reemplazar varias teorías aparentemente diferentes por una única teoría con muchas soluciones.

BRANAS DE CUALQUIER DIMENSION

¿Qué hay de especial en las cuerdas? ¿Qué hay en los filamentos unidimensionales de energía para que los teóricos estén tan seguros de que son los bloques constituyentes de toda la materia? Cuanto más sabemos de la teoría, más seguros vamos estando que no hay nada muy especial en ellas. La mágica, misteriosa y asombrosa teoría M es oncedimensional. Esa teoría no tiene cuerdas en absoluto. Tiene membranas y gravitones, pero no cuerdas. Como vimos, las cuerdas aparecen sólo cuando compactifícamos la teoría M, e incluso entonces las cuerdas son tan sólo límites de membranas tipo cinta que sólo se hacen verdaderamente parecidas a cuerdas cuando la dimensión compacta se contrae hasta un tamaño prácticamente nulo. En otras palabras, la teoría de cuerdas es una teoría de cuerdas únicamente en ciertas regiones límite del paisaje.

En un mundo con tres dimensiones espaciales hay tres tipos de objetos que los teóricos de cuerdas llaman branas. El más simple es una partícula puntual. Puesto que un punto no tiene extensión en ninguna dimensión, es habitual considerar el punto como un espacio cerodimensional. La vida en un punto sería muy aburrida: no hay direcciones que explorar. Los teóricos de cuerdas llaman a las partículas puntuales 0-branas, donde el 0 representa la dimensionalidad de la partícula. En el lenguaje de la teoría de cuerdas, una 0-brana, en la que las cuerdas pueden terminar, se denomina una D0-brana.

Después de las 0-branas vienen las 1-branas o cuerdas. Una cuerda tiene extensión en solo una dirección. Vivir en una cuerda sigue siendo muy limitado, pero al menos uno tendría una dimensión en la que moverse. Hay dos tipos de 1-branas en teoría de cuerdas: las cuerdas originales y las D1-cuerdas (los objetos unidimensionales en donde pueden terminar las cuerdas ordinarias). Finalmente hay 2-branas, o membranas, hojas de materia flexibles.

La vida es infinitamente más variada en una 2-brana, pero aún no tan interesante como en el espacio tridimensional. De hecho, podíamos llamar a nuestro mundo tridimensional una 3-brana pero, a diferencia de las 0, 1 y 2-branas, no podemos mover la 3-brana en el espacio. Es espacio. Pero supongamos que viviéramos en un mundo con cuatro dimensiones espaciales. La dirección extra del espacio daría a una 3-brana libertad para moverse. En un mundo con cuatro dimensiones, es posible tener 0, 1, 2 y 3-branas.

¿Qué pasa en el mundo 9+1 dimensional de la teoría de cuerdas? Es posible que las branas pudieran existir en todo el recorrido desde las 0-branas a las 8-branas. Esto no significa en sí mismo que una teoría dada tenga realmente tales objetos; eso depende de los constituyentes básicos de la materia y de cómo pueden ensamblarse. Pero sí significa que hay dimensiones suficientes para contener tales branas. Las diez direcciones espaciales de la teoría M son suficientes para contener un tipo más de brana: la 9-brana.

El hecho de que diez tipos diferentes de branas pueden encajar en las diez dimensiones del espacio no significa que la teoría M tenga realmente a todas ellas como objetos posibles. De hecho, la teoría M no lo hace. Es una teoría de gravitones, membranas y 5-branas. No existen otras branas. Explicar por qué nos llevaría muy lejos en las matemáticas abstractas de la relatividad general supersimétrica, pero no necesitamos llegar a ello: basta con saber que la supergravedad oncedimensional (es decir, 10+1 dimensional) es una teoría de membranas y 5-branas que interaccionan gravitatoriamente lanzando gravitones de un lado a otro.

Cada una de las teorías de cuerdas decadimensionales tiene una variedad de D-branas. Una versión —la teoría de cuerdas Tipo IIa—tiene membranas de dimensión par: D0, D2, D4, D6 y D8. La teoría tipo IIb tiene branas de dimensión impar: D1, D3, D5, D7 y D9. Igual que se podría atar más de una comba al mismo eje, cualquier número de cuerdas puede terminar en una D-brana. De hecho, una única cuerda puede tener sus dos extremos atados a la misma D-brana de la misma forma que los dos extremos de una comba podrían estar atados al mismo eje. Estos segmentos de cuerda estarían libres para moverse a lo largo de la brana, pero no podrían abandonarla. Son criaturas confinadas a vivir su vida en la D-brana.

Lo que hace tan interesantes a estos pequeños segmentos de cuerda es que se comportan igual que partículas elementales. Tomemos, por ejemplo, D3-branas. Las cuerdas cortas, con ambos extremos atados a la brana, son libres de moverse a lo largo del volumen tridimensional de la D3-brana. Pueden juntarse, unirse para formar un único segmento, vibrar y desconectarse. Se mueven e interaccionan igual que las partículas para cuya explicación fue ideada originalmente la teoría de cuerdas. Pero ahora viven en una brana.

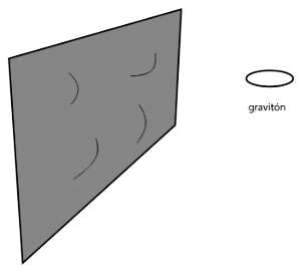
La D-brana es un modelo de un mundo con partículas elementales que se comportan de forma muy parecida a las partículas elementales reales. La única cosa que falta en la D-brana es la gravedad. Ello se debe a que el gravitón es una cuerda cerrada, una cuerda sin extremos. Una cuerda sin extremos no estaría pegada a la brana. ¿Podría el mundo real de electrones, fotones y todas las demás partículas elementales (con la excepción del gravitón) —así como átomos, moléculas, personas, estrellas y galaxias— tener lugar en una brana? Para la mayoría de los teóricos que trabajan en estos problemas, esto parece la posibilidad más probable.

BRANAS Y COMPACTIFICACION

Con branas pueden hacerse todo tipo de cosas. Tomemos una D2-brana —una membrana— y curvémosla para formar una 2-esfera.Habremos hecho un globo. El problema es que la tensión de la membrana hace que desaparezca rápidamente, como un globo pinchado. Podríamos dar a la D2-brana la forma de un toro, pero también éste colapsaría. Pero imaginemos ahora una brana que se extiende de un extremo a otro del universo. El ejemplo más simple de visualizar es una D1-brana infinita extendida a través de todo el universo como un cable infinito. Una D-brana infinita no tiene manera de contraerse y desaparecer. Podemos imaginar que dos gigantes cósmicos mantienen fijos sus extremos, pero puesto que la D-brana es infinita, los gigantes están infinitamente alejados.

No hay por qué detenerse en D1-branas: una hoja infinita extendida a través del universo también es estable. Esta vez necesitaríamos muchos gigantes para mantener fijos los bordes pero, de nuevo, estarían infinitamente alejados. La membrana infinita sería un mundo con partículas elementales que podría parecerse a una versión «planilandesa» de nuestro propio universo. Quizá usted piense que las criaturas de la membrana no tendrían ninguna forma de saber que existen más dimensiones, pero eso no es completamente cierto. Las dimensiones serían delatadas por las propiedades de la fuerza gravitatoria. Recordemos que la gravedad es debida a gravitones que saltan entre los objetos. Pero los gravitones son cuerdas cerradas sin extremos. No tienen ninguna razón para adherirse a la brana. En su lugar, viajan libremente por todo el espacio. Pueden seguir siendo intercambiados entre objetos en la brana pero solamente si viajan a través de las dimensiones extra y luego vuelven a la brana. La gravedad sería como un «mensaje» de ciencia-ficción que dice a las criaturas planilandesas que hay más dimensiones y que ellas están prisioneras en una superficie bidimensional.

Las dimensiones «inobservadas» de la gravedad serían de hecho fáciles de detectar. Cuando los objetos colisionan, pueden radiar gravitones, igual que los electrones radian fotones cuando colisionan. Pero normalmente los gravitones radiados escaparán al espacio y nunca volverán a la brana. De este modo se perdería la energía de la brana. Las criaturas planilandesas descubrirían que la energía no se convierte en calor, energía potencial o energía química; simplemente desaparece.

Imaginemos ahora que el espacio tiene más dimensiones que las tres usuales. D3-branas infinitas podrían extenderse a través del espacio de la misma manera, y en una 3-brana podrían existir todas las cosas habituales de nuestro mundo, excepto que la gravedad sería errónea. La ley de la fuerza gravitatoria reflejaría el hecho de que el gravitón se mueve a través de más dimensiones. La gravedad estaría «diluida» por dispersarse en las dimensiones extra. El resultado sería calamitoso. La gravedad sería mucho más débil, y galaxias, estrellas y planetas estarían pobremente unidos. De hecho, la gravedad sería demasiado débil para mantenernos en la Tierra incluso si la Tierra se mantuviera unida de algún modo.

Tomemos las dimensiones extra —las que nosotros no podemos explorar pero sí puede hacerlo el gravitón— y enrollémoslas en un espacio compacto microscópicamente pequeño. Las tres dimensiones de la experiencia ordinaria forman una habitación infinita, pero las otras direcciones tienen paredes, techos y suelos. Los puntos en paredes opuestas o en el techo y el suelo están emparejados. Para ayudar a la visualización, volvamos al ejemplo en el que compactificábamos el espacio tridimensional enrollando una dirección. Empezando con una habitación infinita, cada punto del techo se identificaba con el punto del suelo que tiene directamente debajo. Pero ahora el suelo tiene una alfombra que se extiende hasta el infinito en infinitas direcciones. La alfombra es una D-brana. Imaginemos que la alfombra-brana se mueve lentamente en la dirección vertical. Se eleva lentamente desde el suelo como una alfombra mágica en las Las mil y una noches. Sigue levitando y ascendiendo hasta que toca el techo. Y abracadabra. La alfombra reaparece instantáneamente en el suelo.

El gravitón sigue sin estar unido a la alfombra-brana, pero ahora no puede ir muy lejos. Hay muy poco espacio para moverse en la dimensión extra. Y si la dimensión extra es microscópicamente pequeña, entonces es difícil decir si el gravitón está fuera de la brana. Resultado: la gravedad es casi exactamente la que sería si, como todo lo demás, el gravitón se moviera en la brana. Y, por supuesto, no hay nada nuevo si reemplazamos la membrana por una D3-brana en un espacio de dimensión más alta. Una D3-brana en el espacio nonodimensional de la teoría de cuerdas sería muy similar a nuestro mundo si las dimensiones extra estuvieran apretadamente enrolladas.

La mayoría de los teóricos de cuerdas piensan que realmente vivimos en un mundo-brana que flota en un espacio con seis dimensiones extra. Y quizá hay otras branas flotando cerca, separadas microscópicamente de nosotros pero invisibles (para nosotros) porque nuestros fotones se pegan a nuestra propia brana, y los suyos se pegan a su brana. Aunque invisibles, estas otras branas no serían imposibles de detectar: la gravedad, formada por cuerdas cerradas, salvaría la separación. Pero ¿no es así precisamente la materia oscura: materia invisible cuya atracción gravitatoria es sentida por nuestras propias estrellas y galaxias?

Las D-branas de Polchinski abren todo tipo de nuevas direcciones. Desde nuestro punto de vista, un universo con muchos mundo-branas viviendo pacíficamente unos al lado de otros es tan solo una posibilidad más que puede encontrarse en el paisaje. Espacios de Calabi Yau de complejidad increíble, centenares de moduli, mundo-branas, flujos (aún por llegar): el universo está empezando a parecer un mundo que no podría gustar a muchos. Para parafrasear al famoso físico experimental I. I. Rabi, «¿Quién ha encargado todo esto?» Pero no hemos agotado ni mucho menos todos los ardides y artilugios con los que se puede elucubrar. He aquí otro: además de flotar en el espacio compacto, las branas también pueden estar enrolladas en las direcciones compactas. El ejemplo más simple es volver al cilindro infinito y enrollar una D1-brana a su alrededor.

Esto sería lo mismo que enrollar una cuerda ordinaria alrededor del cilindro, excepto que la cuerda está reemplazada por una D1-brana. Este objeto, visto a distancia, se parecería a una partícula puntual en una línea unidimensional. Por el contrario, supongamos que el espacio compacto fuera una 2-esfera ordinaria. Podríamos tratar de enrollar una cuerda o una D1-brana alrededor del ecuador de la esfera como un cinturón alrededor de la cintura de un hombre gordo. Pero el cinturón podría resbalar y soltarse del hombre gordo. Una cuerda o una D1-brana enrollada en una esfera no es estable, no se quedaría allí mucho tiempo. En palabras del físico Sidney Coleman, «No se puede poner un lazo a un balón de baloncesto».

¿Qué pasa con el toro —la superficie de una rosquilla? ¿Puede enrollarse una D1-brana en el toro de una forma estable? Sí y, además, en más de una forma. Hay dos formas de «poner un cinturón a la rosquilla». Una manera es pasar el cinturón por el agujero. Inténtelo. Tome una rosquilla o un donut y pase una cuerda a través del agujero. Enróllela y átela. La cuerda no puede escaparse. ¿Puede ver la otra manera de poner el cinturón al toro? El factor decisivo es la «topología» del toro. La topología es la disciplina matemática que distingue esferas de toros) y espacios más complicados.

Una extensión interesante del toro es una superficie con dos agujeros. Tomemos un trozo de arcilla y moldeemos una bola. La superficie es una esfera. Ahora hagamos un agujero que la atraviese de modo que se parezca a un donut: la superficie es un toro. A continuación, hagamos un segundo agujero: la superficie es una generalización doblemente agujereada de un toro. Hay más formas de enrollar una D1-brana en el toro doblemente agujereado que en el toro con un agujero. Un matemático llamaría a la esfera una superficie de género cero, al toro una superficie de género uno y, al toro de dos agujeros, una superficie de género dos. Cuanto más alto es el género, más maneras hay de enrollar branas.

Teniendo nueve dimensiones espaciales, la teoría de cuerdas tiene seis dimensiones extra a ocultar por compactificación. Los espacios hexadimensionales son enormemente más complicados que los espacios bidimensionales. No solo se pueden enrollar DI-branas sino que también hay versiones en dimensiones más altas de donuts con agujeros que le permitirán enrollar D2, D3, D4, D5 y D6-branas en cientos de maneras.

Hasta ahora hemos considerado básicamente branas de una en una. Pero podemos tener montones de ellas. Pensemos en la alfombra en una habitación infinita. ¿Por qué no tener dos alfombras, una encima de la otra? De hecho es posible apilarlas como pilas de alfombras en un bazar persa. Igual que las alfombras podrían flotar libremente por separado, una pila de D-branas puede separarse en varias branas que flotan libremente. Pero las D-branas se parecen un poco a alfombras pegajosas. Si usted las junta, se pegan, formando una brana compuesta. Puede colocar varias alfombras apiladas a diferentes alturas en la habitación. Tiene nueva flexibilidad para hacer mundos con todo tipo de propiedades.

De hecho, con cinco alfombras, pegadas en un pila de dos y otra de tres, puede hacer un mundo con leyes de la física que tienen muchas similitudes con el modelo estándar. Las localizaciones de las branas en el espacio compacto son nuevas variables que añadir a los módulos cuando se cuentan las posibilidades para crear un universo. Vistas a distancia, cuando las direcciones compactas son microscópicas —demasiado pequeñas para ver—, las posiciones de la brana parecen ser simples campos escalares adicionales que definen el paisaje.