
MULTIVERSO NIVEL 4

¿Por qué estas ecuaciones y no otras?
El viejo sueño de la Física es unificar todas las leyes físicas en una «teoría del todo». El empleo de sus ecuaciones matemáticas permite responder a las complejas preguntas que quitan el sueño a los físicos de hoy, como el funcionamiento de la gravitación cuántica y la resolución del problema de la medida. John Wheeler se hizo una pregunta que aún no se ha respondido: ¿Por qué esas ecuaciones en particular y no otras? Existe una hipótesis, la hipótesis del Universo matemático (HUM), según la cual nuestra realidad física exterior es una estructura matemática, y esto agudiza el interrogante de Wheeler. Los matemáticos han descubierto gran cantidad de estructuras matemáticas. La figura 1 ilustra algunas de las más simples en forma de cajas. Ninguna de las que aparecen en la figura concuerda con nuestra realidad física, por mucho que algunas de ellas alcancen a describir determinados aspectos limitados de este mundo.
En 1916, la caja etiquetada como «RELATIVIDAD GENERAL» se consideró una buena candidata para lograr una concordancia perfecta, porque no solo contenía espacio y tiempo, sino también varias clases de materia; sin embargo, el descubrimiento de la mecánica cuántica no tardó en evidenciar que nuestra realidad física porta aspectos inexistentes en esa estructura matemática particular. Por suerte, ahora podemos ampliar la figura añadiéndole esta estructura, sabiendo que esta caja nueva en la figura es la caja, la que se corresponde con nuestra realidad física.
FIGURA 1
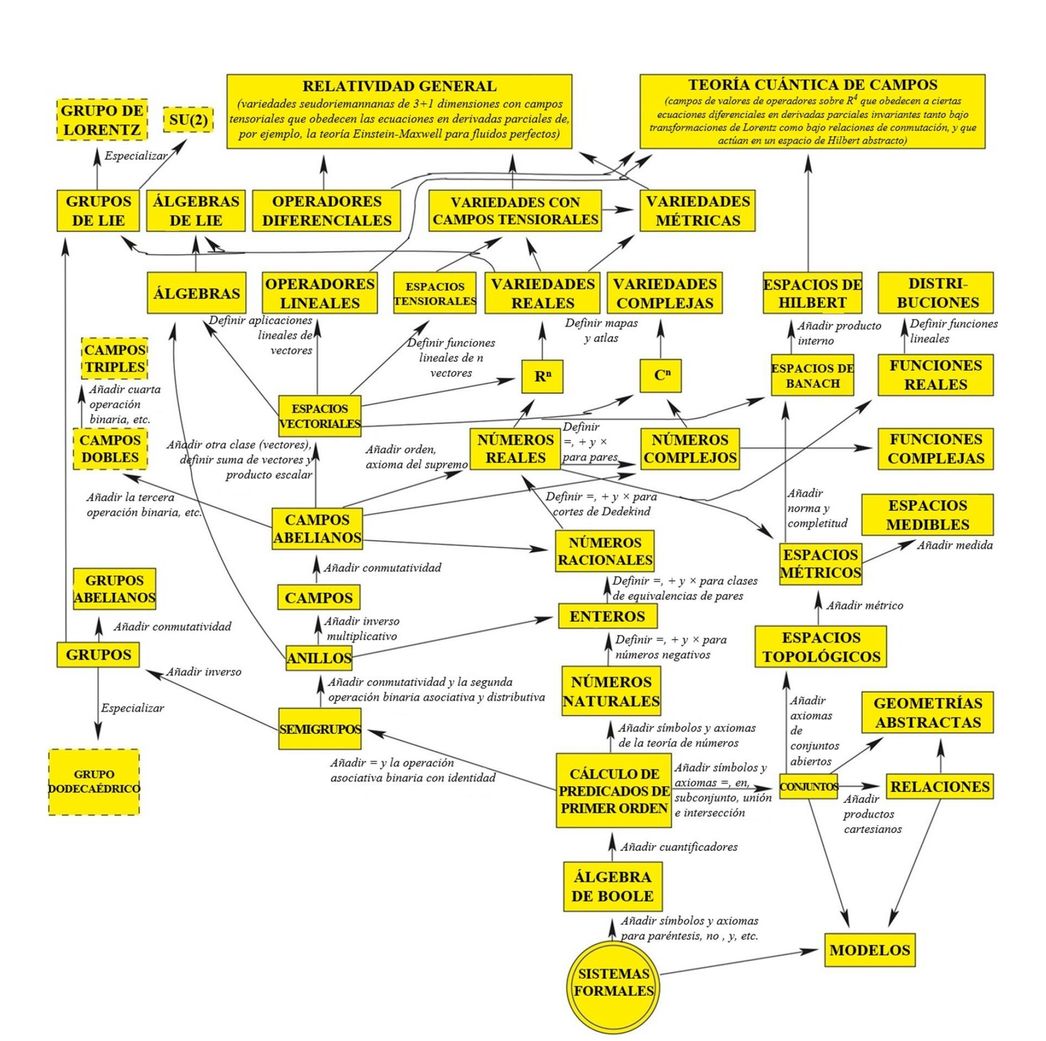
Relaciones entre varias estructuras matemáticas básicas. Las flechas indican en general la adición de nuevos símbolos y/o axiomas. La unión de dos flechas indica la combinación de estructuras; por ejemplo, "u" álgebra es un espacio vectorial que también es un anillo, y un grupo de Lie es un grupo que también es una variedad. Lo más probable es que el conjunto íntegro del árbol genealógico tenga una extensión infinita; la figura solo ilustra una pequeña muestra cercana a la base
¿Y qué hay del resto de cajas? Si la nueva caja se corresponde con una realidad física existente, ¿por qué las demás no? Todas las cajas se sitúan en un nivel matemático equitativo, el correspondiente a distintas estructuras matemáticas, de modo que ¿por qué razón unas tendrían que ser más iguales que otras cuando se trata de la existencia física? ¿De verdad podría haber una asimetría fundamental, existencial, inexplicada, inherente a la mismísima esencia de la realidad que divida las estructuras matemáticas en dos clases, las que tienen existencia física y las que no?
Democracia matemática
Hay una vía para salir de este rompecabezas filosófico, y es suponer que hay una democracia matemática absoluta: que la existencia matemática y la existencia física son equivalentes, de modo que todas las estructuras que existen en el ámbito matemático también existen en el ámbito físico. Así que el resto de cajas de la figura 1 también describe un Universo físico real, solo que uno distinto del que casualmente habitamos nosotros. Esto se puede interpretar como una forma de platonismo radical, pues afirma que todas las estructuras matemáticas del «mundo de las ideas» de Platón existen «ahí fuera» en un sentido físico.
En otras palabras, la idea es que existe un cuarto nivel de Universos paralelos que es mucho más extenso que los tres que hemos visto hasta ahora y que se corresponde con las distintas estructuras matemáticas. Los tres primeros niveles se corresponden con Universos paralelos incomunicados dentro de la misma estructura matemática: el nivel I se refiere sencillamente a regiones distantes desde las que la luz aún no ha tenido tiempo de alcanzarnos; el nivel II cubre regiones eternamente inalcanzables debido a la inflación cosmológica del espacio intermedio, y el nivel III, la «pluralidad de mundos» de Everett, guarda relación con partes incomunicadas del espacio de Hilbert de la mecánica cuántica. Mientras que todos los Universos paralelos de los niveles I, II y III se rigen por las mismas ecuaciones matemáticas fundamentales (que describen la mecánica cuántica, la inflación, etc.), los Universos paralelos del nivel IV bailan al son de ecuaciones diferentes, correspondientes a estructuras matemáticas distintas.
La figura 2 ilustra esta jerarquía de cuatro niveles de Multiverso. La hipótesis del Universo matemático implica el especulativo Multiverso del nivel IV. Si la teoría de que existe el Multiverso del nivel IV es correcta, entonces, como no tiene ni un solo parámetro libre, un matemático infinitamente inteligente podría, en principio, deducir todas las propiedades de todos los Universos paralelos (incluidas las percepciones subjetivas de las subestructuras autoconscientes que albergan). Pero ¿es correcta esta teoría?
FIGURA 2
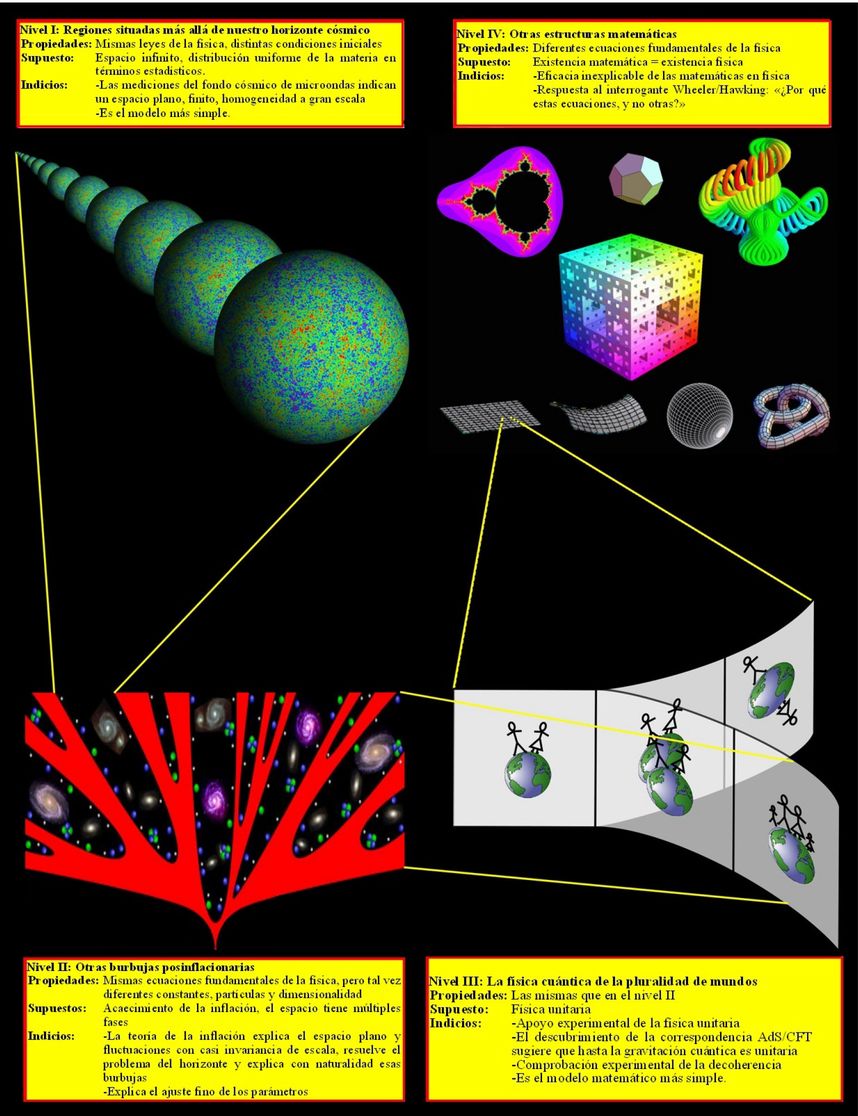
¿De verdad existe el Multiverso del nivel IV?
Curiosamente, en el contexto de la hipótesis del Universo matemático (HUM), la existencia del Multiverso del nivel IV no es opcional. La HUM dice que una estructura matemática es nuestra realidad física exterior, y no una mera descripción de la misma. Esta equivalencia entre la existencia física y la matemática significa que si una estructura matemática contiene una subestructura autoconsciente, esta se percibirá existiendo dentro de un Universo físico real, aunque en general se tratará de un Universo con unas propiedades diferentes a las del nuestro. A la pregunta que planteó Stephen Hawking: «¿Qué es lo que insufla fuego a las ecuaciones y crea un Universo para que ellas lo describan?», se puede objetar lo siguiente: la HUM no requiere insuflar ningún fuego, porque la clave no estriba en que una estructura matemática describe un Universo, sino en que es un Universo.
Es más, tampoco es necesario crear nada. No se puede crear una estructura matemática, sino que existe sin más. No existe en el espacio ni en el tiempo, el espacio y el tiempo pueden existir en ella. En otras palabras, todas las estructuras que existen en términos matemáticos tienen el mismo estatus ontológico, y la cuestión más interesante no es cuáles existen físicamente (todas ellas lo hacen), sino cuáles albergan vida, y tal vez a nosotros. Muchas estructuras matemáticas carecen de complejidad suficiente para mantener alguna clase de subestructura autoconsciente, así que es muy probable que el Multiverso del nivel IV se parezca a un vasto y casi inhabitable desierto donde la vida está confinada a raros oasis, estructuras matemáticas aptas para la vida como la que habitamos nosotros. Encontramos signos de que el Multiverso del nivel II es en su mayoría un páramo estéril donde la autoconsciencia está confinada a la diminuta fracción del espacio donde el valor de la densidad de la energía oscura y otros parámetros físicos son justo los adecuados para la vida. En el Multiverso del nivel I, la historia parece repetirse porque la vida prospera sobre todo en la reducida fracción de espacio cercana a superficies planetarias. Por tanto, ¡los humanos nos encontramos realmente en un lugar muy privilegiado!
Exploración del Multiverso del nivel IV: ¿qué hay ahí fuera?
Nuestro vecindario más inmediato
Aunque aún no sabemos en qué estructura matemática exacta residimos, no es difícil imaginar numerosas modificaciones menores que darían lugar a otras estructuras matemáticas válidas. Por ejemplo, el modelo estándar de la Física de partículas implica ciertas simetrías que los matemáticos denominan SU(3) × SU(2) × U(1), y si las sustituimos por simetrías distintas, obtendremos una estructura matemática con diferentes tipos de partículas y fuerzas, donde quarks, electrones y fotones sean reemplazados por otras entidades con otras propiedades. En algunas estructuras matemáticas no hay luz. En otras, no hay gravitación. En la descripción matemática de Einstein del espaciotiempo, los números 1 y 3, que especifican respectivamente la cantidad de dimensiones temporales y espaciales, se pueden sustituir por distintos valores a nuestro antojo.
La inflación de una sola estructura matemática, con su conjunto particular de leyes fundamentales de la Física, puede dar lugar a diferentes leyes efectivas de la Física en distintas partes del espacio, y formar así un Multiverso del nivel II. Ahora hablamos de algo más radical, donde cambian incluso las leyes fundamentales, donde, por ejemplo, no hay mecánica cuántica. Si la teoría de cuerdas se puede definir con rigor a través de las matemáticas, entonces existe una estructura matemática donde la teoría de cuerdas es la «teoría del todo correcta», pero no lo es en ningún otro lugar del Multiverso del nivel IV.
Para contemplar el extraño Multiverso del nivel IV hay que dejar volar la imaginación, libre de cualquier idea preconcebida sobre cómo se supone que son las leyes de la Física. Consideremos el espacio y el tiempo: en lugar de ser continuos, tal como sugiere nuestro mundo, pueden ser discretos. Se ha especulado mucho con la idea de que incluso nuestro propio Universo tal vez exhiba alguna suerte de discretización espaciotemporal oculta a escalas tan pequeñas que aún no la hemosdetectado. Siendo más radicales todavía, hay muchas estructuras matemáticas que prescinden por completo del espacio y el tiempo, así que en ellas no sucede nada significativo.
Una estructura matemática no es más que un conjunto de elementos abstractos que mantienen relaciones entre sí. Para efectuar un análisis sistemático del Multiverso del nivel IV, se puede escribir un programa de ordenador que genere de manera automática una lista con las estructuras matemáticas que existen, empezando por las más simples y siguiendo de forma progresiva hasta las más complejas. Todas y cada una de esas estructuras matemáticas se pueden identificar mediante un número unívoco: su número de línea dentro de una lista maestra. En el caso de las estructuras matemáticas finitas, todas las relaciones se pueden describir mediante tablas finitas de números, lo que generaliza la idea de la tabla de multiplicar a otros tipos de relaciones. Con estructuras formadas por gran cantidad de elementos, estas tablas se vuelven grandes y abultadas, lo que genera cifrados enormes que acaban en puestos muy avanzados de la lista. En cambio, una pequeña fracción de estas estructuras tan largas contiene una simplicidad elegante que facilita mucho su descripción.
Consideremos, por ejemplo, la estructura matemática cuyos elementos sean los números 0, 1, 2, 3… y donde las relaciones sean la suma y la multiplicación. Sería un despilfarro especificar cómo funciona la multiplicación escribiendo una inmensa tabla de multiplicar para todos los pares de números: aunque nos limitáramos al primer millón de números, necesitaríamos una tabla con un millón de filas y un millón de columnas, la cual contendría un billón de entradas. En lugar de hacer eso, enseñamos a los niños en edad escolar una tabla de multiplicar para los 10 primeros números y un sencillo algoritmo para que sepan usarla para multiplicar números mayores con más de un dígito. A los ordenadores les describimos la multiplicación de un modo mucho más eficiente que a los niños: representando los números en sistema binario, lo que tan solo nos obliga a especificar una tabla de multiplicar de 2 × 2 para ceros y unos, y un escueto programa de ordenador que especifica cómo usarla para multiplicar números de cualquier tamaño.
En resumen, el Multiverso del nivel IV se puede cartografiar de manera sistemática mediante la enumeración de estructuras matemáticas con un ordenador y el estudio de sus propiedades. Si algún día logramos identificar en qué estructura matemática residimos, entonces podremos referirnos a ella por su número dentro de la lista general, y especificar por primera vez nuestra dirección dentro del conjunto completo de la realidad física.
La estructura del Multiverso del nivel IV

Dentro de su carácter especulativo, resulta interesante estudiar el Multiverso del nivel IV. Si aceptamos la definición formalista más extendida de las matemáticas como «el estudio de estructuras matemáticas», entonces lo que hacen los matemáticos a diario para ganarse la vida es estudiar el Multiverso del nivel IV. Para un físico que cree en la hipótesis del Universo matemático, su estudio equivale asimismo a explicar la realidad física última y buscar qué lugar ocupamos dentro de ella. Y, tal como corresponde, es más fácil explorar el Multiverso del nivel IV que cualquier otro Multiverso inferior o incluso nuestro propio Universo, porque para ello no se necesitan cohetes ni telescopios, basta con ordenadores e ideas (más o menos descabelladas). Al llevar esto a la práctica nos encontramos ante una cantidad enorme de redundancias. Existen muchas maneras de escribir un programa informático para que ejecute un cálculo determinado, y hay una cantidad igual de grande de maneras equivalentes de describir estructuras matemáticas finitas mediante tablas de números, que se corresponden, por ejemplo, con distintas maneras de ordenar/etiquetar los elementos.
Una estructura matemática es una clase de equivalencia entre descripciones, de modo que la lista maestra debería contener cada estructura matemática tan solo una vez, especificada únicamente por aquella de sus numerosas descripciones equivalentes que fuera más breve. A partir de dos estructuras matemáticas cualesquiera, se puede definir una nueva mediante la combinación de sus elementos y relaciones. Muchas de las estructuras que figuran en la lista maestra son de esta clase compuesta, y para estudiar el Multiverso del nivel IV tiene sentido ignorarlas. Esto es así porque no hay relaciones que conecten ambas partes, lo que significa que un observador autoconsciente en una de esas partes no será jamás consciente de la existencia de la otra parte, ni se verá afectado por ella, de modo que también podrá actuar como si la otra parte no existiera (o no formara parte de su estructura matemática). El único motivo por el que podrían importar las estructuras compuestas sería si intervinieran en la resolución del problema de la medida, lo que alteraría la probabilidad que le asignaríamos de residir en estructuras matemáticas distintas. Como una estructura compuesta es más complicada de describir, lo normal es que aparezca en un puesto mucho más avanzado dentro de la lista maestra que sus partes, lo que daría una «medida» más baja.
De hecho, para cualquier cantidad finita de estructuras en el Multiverso del nivel IV, también hay una estructura compuesta única situada muchísimo más abajo dentro de la lista maestra que las contiene todas. Aunque las distintas estructuras matemáticas del Multiverso del nivel IV no mantienen ninguna conexión física, hay muchas relaciones interesantes entre ellas en el metanivel. Por ejemplo, acabamos de ver que algunas consisten en la combinación de otras. Otro ejemplo es que una estructura puede describir otra en un sentido determinado: los elementos de la primera estructura pueden corresponderse con las relaciones que se dan en la segunda, y las relaciones en la primera pueden describir lo que ocurre cuando se combinan relaciones en la segunda.
Los límites del Multiverso del nivel IV: indecidible, incomputable e indefinido
¿Qué dimensiones tiene el Multiverso del nivel IV? Para empezar, hay una cantidad infinita de estructuras matemáticas finitas. Una cantidad igual de infinita que los números 1, 2, 3…, para ser más precisos, ya que acabamos de ver que se pueden relacionar en una sola lista numerada. Pero ¿cuántas estructuras matemáticas infinitas formadas por una cantidad infinita de elementos contiene el Multiverso del nivel IV? Hemos visto que algunas estructuras infinitas también se pueden definir e incluir en la lista maestra junto con las estructuras finitas, mediante el empleo de programas informáticos que definan sus relaciones. Sin embargo, la inclusión del infinito abre una caja de Pandora repleta de problemas ontológicos. Para verlo, consideremos una estructura matemática cuyos elementos sean los números 1, 2, 3… que incluya las tres relaciones (funciones) de la siguiente lista, reglas que toman los números como entrada y calculan un nuevo número siguiendo las definiciones relacionadas en la lista:
1. P(n): Dado un número n, P(n) denota el número primo más bajo que es mayor que n.
2. G(n): Dado un número n, G(n) denota el primo gemelo más bajo que es mayor que n (un primo gemelo es un número primo separado de otro número primo por un número intermedio; 11 y 13 son un ejemplo de par de primos gemelos).
3. H(m,n): Dados dos números m y n, H(m,n) vale 0 si el programa informático que ocupa el puesto m en la lista maestra de todos los programas informáticos seguirá ejecutándose eternamente al proporcionarle los bits de n como entrada, y H(m,n) vale 1 si, por el contrario, el programa se detiene tras una cantidad finita de pasos.
¿Es apta esta estructura para formar parte del Multiverso del nivel IV, o no está lo bastante bien definida? La primera función, P(n), es fácil: es sencillo escribir un programa que empiece comprobando si los números que siguen a n son primos, y que se detenga en cuanto encuentre uno que lo sea. Y es indudable que tal programa se detendrá después de una cantidad finita de pasos, porque sabemos que existe una infinidad de números primos (un hecho demostrado por Euclides más de dos mil años atrás). Así que P(n) es un ejemplo de lo que se denomina una función computable.
La segunda función, G(n), es más delicada: nuevamente resulta sencillo escribir un programa que analice todos los números que siguen a n para comprobar si alguno de ellos forma parte de un par de primos gemelos, pero si introducimos en el programa un número n mayor que 37 568 016 956 852 666 669 −1 , no habrá ninguna garantía de que el programa llegue a detenerse en algún momento y dé un resultado porque, a pesar de los enormes esfuerzos de los matemáticos más perspicaces, seguimos sin saber si existe una cantidad infinita de números primos gemelos. Así que por ahora desconocemos si G(n) es una función computable y, por tanto, si está definida con rigor, y es discutible si una estructura matemática que contenga una relación con una especificación tan laxa se puede considerar bien definida.
La tercera función, H(m,n), resulta aún más nefasta: los iniciadores de las ciencias de la computación Alonzo Church y Alan Turing determinaron que no existe ningún programa capaz de computar H(m,n) con la introducción arbitraria de números m y n en una cantidad finita de pasos, de modo que H(m,n) es un ejemplo de lo que se denomina una función no computable. En otras palabras, no hay ningún programa capaz de concretar qué otros programas acabarán deteniéndose. Desde luego, cualquier programa dado acabará deteniéndose o no, pero la clave está en que, al igual que con los primos gemelos, habría que esperar eternamente para saberlo.
El descubrimiento Church-Turing de las funciones no computables está muy relacionado con el hallazgo por parte del gran Kurt Gödel de que algunos teoremas aritméticos son indecidibles, lo que significa que ni pueden demostrarse ni pueden refutarse en una cantidad finita de pasos. ¿Cabría considerar una estructura matemática como bien definida aun cuando contenga una relación como H que ni siquiera se puede valorar con un ordenador de una capacidad ilimitada? En tal caso, la estructura solo sería cognoscible para una entidad a modo de oráculo que de algún modo dispusiera de poderes infinitos y fuera capaz de efectuar una cantidad realmente infinita de pasos computacionales para llegar a una respuesta.
Tales estructuras jamás aparecen en la lista maestra de la que hablamos antes, la cual abarca tan solo estructuras definibles mediante programas informáticos convencionales, y no las que precisan los poderes infinitos propios de un oráculo.
Por último, consideremos una de las estructuras matemáticas más populares de nuestro tiempo: la de los llamados números reales, como 3,141592…, cuyos decimales no se acaban nunca. Forman un continuo, y para especificar incluso un único elemento hay que relacionar una cantidad infinita de decimales, es decir, una cantidad infinita de información. Esto significa que los programas informáticos convencionales son absolutamente incapaces de procesarlos: el problema no estriba tan solo en ejecutar una cantidad infinita de pasos computacionales sobre una entrada finita, como en el ejemplo de H, sino en introducir y extraer una cantidad infinita de información.
Por otro lado, el trabajo de Kurt Gödel debería hacernos temer que la HUM carezca de sentido con estructuras matemáticas infinitas porque, en cierto modo, nuestro Universo sería incoherente o indefinido. Si aceptamos el aforismo del matemático David Hilbert de que «la existencia matemática consiste tan solo en estar libre de contradicciones», entonces una estructura incoherente no existiría en el mundo matemático, y no digamos ya en el mundo físico de la HUM. El modelo físico estándar actual incluye a diario estructuras matemáticas tales como los números enteros y los números reales. Pero el trabajo de Gödel deja abierta la posibilidad de que las matemáticas cotidianas sean incoherentes, y de que exista dentro de la propia teoría de números una demostración con una longitud finita que concluya que 0 = 1. Echando mano de este impactante resultado, cualquier otro enunciado sintácticamente correcto sobre los números enteros se podría demostrar cierto a su vez, y las matemáticas se derrumbarían como un castillo de naipes.
Entonces ¿queda descartada la hipótesis del Universo matemático por el teorema de incompletitud de Gödel? No, al menos no hasta donde sabemos. Gödel evidenció que, dado cualquier sistema formal lo bastante potente, no podemos usarlo para demostrar su propia coherencia, pero eso no significa que sea incoherente en realidad, o que tengamos un problema. De hecho, nuestro cosmos no muestra ningún signo de ser incoherente o de estar mal definido, a pesar de revelar indicios de que es una estructura matemática. Es más: ¿qué esperábamos? Aunque un sistema formal pudiera emplearse para demostrar su propia coherencia, seguiríamos sin convencernos de su verdadera coherencia, puesto que un sistema incoherente puede demostrar cualquier cosa, incluso su coherencia. Podríamos convencernos si un sistema más simple cuya coherencia nos infundiera mayor confianza pudiera demostrar la coherencia de un sistema más poderoso pero, como era de esperar, eso es imposible, tal como también demostró Gödel. Todas estas incertidumbres sobre la indecidibilidad e incoherencia se aplican tan solo a estructuras matemáticas con una cantidad infinita de elementos.
El problema de la medida que invade la cosmología moderna también se aplica tan solo a estructuras matemáticas con una cantidad infinita de elementos, lo que plantea un interrogante sugestivo: ¿son las infinidades, la indecidibilidad, la incoherencia potencial y el problema de la medida verdaderamente inherentes a la realidad física última, o son meros espejismos, productos de nuestros juegos con fuego y del empleo de herramientas matemáticas potentes que resultan más adecuadas para trabajar con ellas que para describir realmente nuestro Universo? Más en concreto ¿hasta qué punto deben estar bien definidas las estructuras matemáticas para ser reales, es decir, para ser miembros del Multiverso del nivel IV? Existe una gradación de opciones interesantes para determinar la aptitud de las estructuras:
Ninguna estructura (es decir, la hipótesis del Universo matemático es falsa).
Estructuras finitas. Son trivialmente computables, puesto que todas sus relaciones se pueden definir mediante tablas de búsqueda finitas.
Estructuras computables (cuyas relaciones se definen mediante cómputos que se detienen).
Estructuras con relaciones definidas mediante cómputos sin la seguridad de que se detengan (pueden requerir una cantidad infinita de pasos), como el ejemplo H.
Estructuras aún más generales, como las que implican un continuo y cuyos elementos habituales precisan una cantidad infinita de información para describirlos.
La hipótesis del Universo computable
Una posibilidad interesante la constituye la hipótesis del Universo computable (en adelante HUC), que tiene su límite en la opción 3 y que no deja lugar para estructuras más generales: hipótesis del Universo computable (HUC), la estructura matemática que se corresponde con nuestra realidad física exterior se define mediante funciones computables. Con esto nos referimos a que todas las relaciones (funciones) que definen la estructura matemática se pueden implementar como cómputos que se detienen con toda seguridad tras una cantidad finita de pasos. Si la HUC es falsa, entonces una hipótesis aún más conservadora la representa la hipótesis del Universo finito (HUF); la opción 2 es su límite: nuestra realidad exterior es una estructura matemática finita.
Los matemáticos han mantenido intensos debates sobre cuestiones relacionadas con todo esto sin hacer ninguna referencia a la Física. Según la escuela finitista de matemáticas, a la que pertenecieron Leopold Kronecker, Hermann Weyl y Reuben Goodstein, un objeto matemático no existe a menos que se pueda construir a partir de números enteros en una cantidad finita de pasos. Esto nos lleva directamente a la opción 3. De acuerdo con la HUC, la estructura matemática que constituye nuestra realidad física tiene la atractiva propiedad de ser computable y, por tanto, de estar bien definida en el sólido sentido de que todas sus relaciones se pueden computar. De ahí se deduce que ningún aspecto físico de nuestro Universo sería incomputable/indecidible, lo que eliminaría el problema de que el trabajo de Church, Turing y Gödel de alguna manera volviera nuestro mundo incompleto o incoherente. No conocemos con exactitud las propiedades de nuestra realidad física, pero esas propiedades existen en el sentido de que están bien definidas.
Muchos autores se han preguntado por qué nuestras leyes físicas parecen bastante simples. Por ejemplo, por qué el modelo estándar de la Física de partículas tiene simetrías tan simples como las que llamamos SU(3) × SU(2) × U(1), las cuales precisan tan solo 32 parámetros, cuando la mayoría de las alternativas son mucho más complicadas. Resulta tentador especular con que la HUC contribuye a esta naturaleza. Mediante la eliminación de todo el continuo, tal vez la HUC ayude también a reducir el paisaje inflacionario y a resolver el problema cosmológico de la medida que está vinculado en gran parte a la capacidad de un verdadero continuo para experimentar un estiramiento exponencial eterno, y producir una cantidad infinita de observadores.
Aunque la HUC posea rasgos atractivos, como garantizar que este Universo está definido con rigor y tal vez mitigar el problema cosmológico de la medida limitando lo que existe, también plantea grandes desafíos que deben resolverse.
Un primer problema relacionado con la HUC es que podría sonar a una renuncia al fundamento filosófico, porque en realidad reconoce que, aunque «ahí fuera» existan todas las estructuras matemáticas posibles, algunas tienen un estatus privilegiado. En cambio, si la HUC resultara ser correcta, sería más bien porque el resto del panorama matemático fuera una mera ilusión, esencialmente indefinido y sencillamente inexistente en cualquier sentido significativo.
Un desafío más inmediato es que el modelo estándar actual (y prácticamente todas las teorías fructíferas a lo largo de la historia) infringe la HUC, y no es nada obvio si existe una alternativa computable viable. El principal quebrantamiento de la HUC proviene de la incorporación del continuo, por lo común en forma de números reales o complejos, lo que ni siquiera permite efectuar la entrada de datos en un proceso de cálculo finito, porque en general se requiere especificar una cantidad infinita de bits. Incluso los planteamientos que intentan desterrar el clásico continuo del espaciotiempo volviéndolo discreto o cuántico, tienden a conservar variables continuas en otros aspectos de la teoría, como la intensidad del campo magnético o la amplitud de la función de onda cuántica.
Un tratamiento interesante de este desafío del continuo implica la sustitución de los números reales por una estructura matemática que emule el continuo pero permanezca computable como, por ejemplo, eso que en matemáticas recibe el nombre de números algebraicos. Otro enfoque que vale la pena explorar consiste en descartar el continuo como algo fundamental y probar a recuperarlo como aproximación. Nunca hemos medido nada en Física con más de 16 dígitos significativos, y tampoco se ha efectuado ningún experimento cuyo resultado dependa de la hipótesis de que exista un verdadero continuo, o que dependa de que la naturaleza compute algo incomputable. Es sorprendente que muchos de los modelos de continuo de la Física matemática clásica (por ejemplo, las ecuaciones que describen ondas, difusión o flujo líquido) se reconozcan explícitamente como meras aproximaciones a una situación real que consiste en un conjunto discreto de átomos subyacente. La investigación en gravitación cuántica sugiere que hasta el espaciotiempo clásico se descompone a escalas muy pequeñas. Por tanto, no podemos estar seguros de que cantidades que seguimos tratando como continuas (como el espaciotiempo, las intensidades de campo y las amplitudes de la función de onda cuántica) no sean meras aproximaciones de algo discreto.
De hecho, determinadas estructuras computables discretas (en realidad, las finitas satisfacen la HUF) se aproximan tan bien a los modelos físicos del continuo, que los físicos las usan para computar cosas en la práctica, lo que deja abierta la cuestión de si la estructura matemática de nuestro Universo se parece más a las anteriores o a estas últimas. Algunos autores han llegado incluso a proponer que las leyes de la naturaleza son computables y finitas, como un autómata celular o una simulación por ordenador. Para rizar más el rizo, la Física también ha brindado ejemplos de continuos (como los campos cuánticos) que producen una solución discreta (como una red cristalina), que a su vez se comporta como un medio continuo a gran escala, que a su vez tiene vibraciones que se comportan como partículas discretas llamadas fonones.
La estructura trascendente del nivel IV
Acabamos de ver la estrecha relación que mantienen las estructuras matemáticas con los cómputos, en tanto que las primeras se definen mediante las segundas. Por otra parte, los cómputos son meros casos especiales de estructuras matemáticas. Por ejemplo, el contenido de información (estado de memoria) de un ordenador consiste en una cadena de bits, como por ejemplo «1001011100111001…», de una extensión inmensa pero finita, equivalente a algún número entero n enorme pero finito escrito en lenguaje binario. El procesamiento de información de un ordenador es una regla determinista para transformar cada estado de memoria en otro (que se aplica una y otra vez), de modo que desde un punto de vista matemático, no es más que una función f que aplica los números enteros consigo mismos: n → f(n) → f(f(n))… En otras palabras, hasta la simulación por ordenador más sofisticada no es más que un caso especial de estructura matemática, y, por tanto, está incluida en el Multiverso del nivel IV.
FIGURA 2
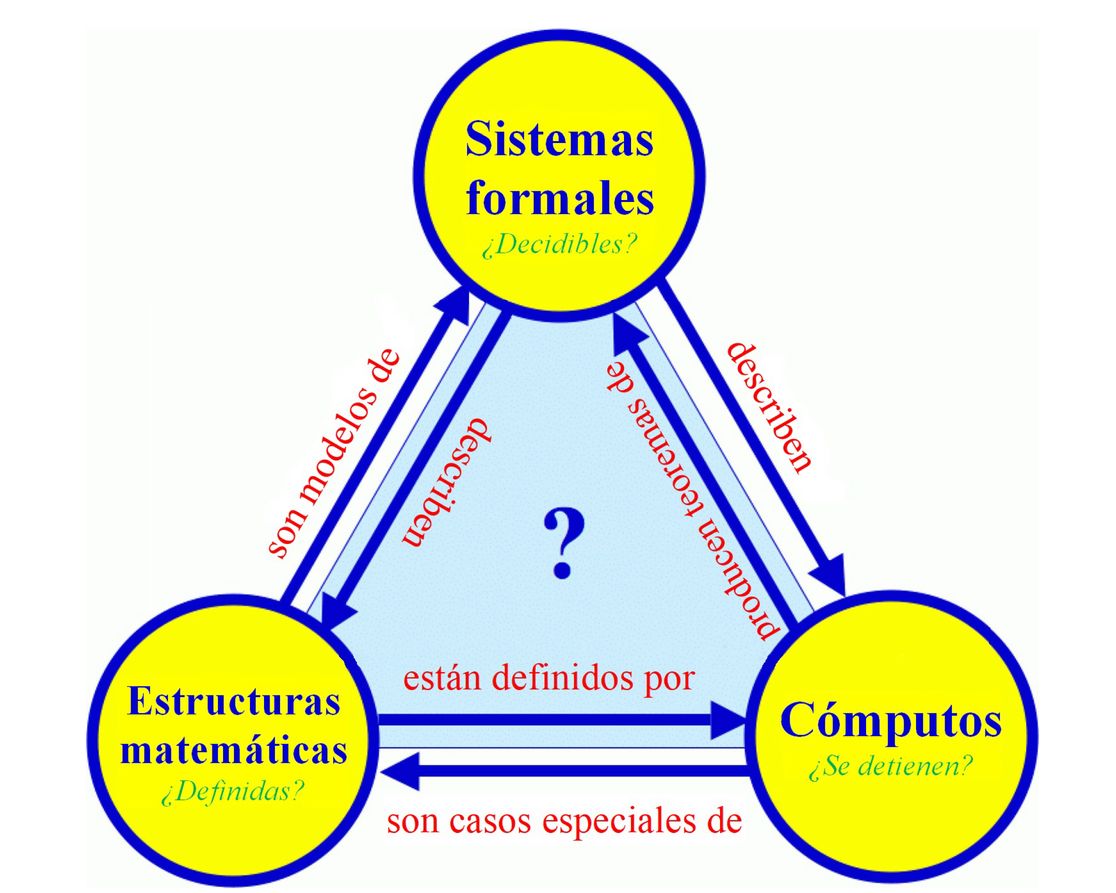
Las flechas indican las estrechas relaciones que se dan entre estructuras matemáticas, sistemas formales y cómputos. El signo de interrogación plantea si todos ellos serán aspectos de la misma estructura trascendente cuya naturaleza aún no hemos desentrañado en su totalidad
La figura 2 ilustra que los cómputos y las estructuras matemáticas no solo están relacionados entre sí, sino también con los sistemas formales, los abstractos sistemas simbólicos de axiomas y reglas de deducción que se usan en matemáticas para demostrar teoremas sobre estructuras matemáticas. Las cajas de la figura 1 se corresponden con esos sistemas formales. Si un sistema formal describe una estructura matemática, en términos matemáticos se dice que la última es un modelo del primero. Es más, los cómputos pueden generar teoremas en sistemas formales (de hecho, para ciertas clases de sistemas formales, existen algoritmos capaces de computar todos los teoremas).
La figura 2 ilustra asimismo que caben problemas potenciales en los tres vértices del triángulo: las estructuras matemáticas pueden tener relaciones indefinidas; los sistemas formales pueden contener enunciados indecidibles; y los cómputos pueden no acabar deteniéndose tras una cantidad finita de pasos. Las relaciones entre los tres vértices con sus complicaciones correspondientes se representan mediante seis flechas. Como cada flecha la estudian distintos especialistas de una variedad de disciplinas que van desde la lógica matemática hasta las ciencias de la computación, el estudio del triángulo como un todo resulta un tanto interdisciplinario y merece más atención.
El signo de interrogación en el centro del triángulo sirve para plantear que los tres vértices (estructuras matemáticas, sistemas formales y cómputos) tal vez no sean más que aspectos diferentes de una estructura trascendente subyacente cuya naturaleza aún no conocemos por completo. Esta estructura (quizá limitada a la parte definida/decidible/ con detención de acuerdo con la HUC) existe «ahí fuera» de un modo libre de todo bagaje, y es tanto la totalidad de lo que tiene existencia matemática como la totalidad de lo que tiene existencia física.
Implicaciones del Multiverso del nivel IV
Simetrías y más allá
Si centráramos la atención en alguna estructura matemática particular de la lista maestra que nos sirve como atlas del Multiverso del nivel IV ¿cómo deduciríamos qué propiedades físicas percibiría en él un observador con consciencia de sí mismo? En otras palabras, ¿cómo haría un matemático infinitamente inteligente para inferir, a partir de su definición matemática, la descripción Física que llamamos «realidad consensuada» Ya dijimos que el primer paso consistiría en calcular las simetrías de la estructura matemática. Las propiedades de simetría se cuentan entre las pocas clases de propiedades comunes a todas las estructuras matemáticas, y pueden manifestarse en forma de simetrías físicas ante los moradores de la estructura.
La cuestión de qué sería lo siguiente que habría que calcular a la hora de estudiar una estructura cualquiera es muy incierta, pero es sorprendente que un estudio más profundo de las simetrías en la estructura matemática particular que habitamos nos haya conducido a nuevos discernimientos. La matemática alemana Emmy Noether demostró en 1915 que cada simetría continua de nuestra estructura matemática conduce a una de las llamadas leyes de conservación de la Física, las cuales garantizan que una cantidad se mantendrá constante, y por tanto tiene la permanencia necesaria para que observadores autoconscientes reparen en ella y le asignen un nombre: «bagaje». Todas las cantidades conservadas se corresponden con esas simetrías: por ejemplo, la energía se corresponde con la simetría de traslación temporal (que las leyes de la Física permanecen iguales en todo momento), la cantidad de movimiento se corresponde con la simetría de traslación espacial (que las leyes se mantienen iguales en todo lugar), el momento angular se corresponde con la simetría rotacional (que el espacio vacío notiene una dirección «arriba» especial) y la carga eléctrica se corresponde con una cierta simetría de mecánica cuántica.
El físico húngaro Eugene Wigner fue más allá para desvelar que estas simetrías también dictan todas las propiedades cuánticas que pueden tener las partículas, incluidas la masa y el espín. En otras palabras, entre ambos, Noether y Wigner evidenciaron que, al menos en nuestra estructura matemática, el estudio de las simetrías revela el «tipo» de materia que puede albergar. A algunos físicos aficionados a la jerga matemática les gusta afirmar que una partícula no es más que «un elemento con una representación irreducible del grupo de simetría». Está claro que prácticamente todas las leyes de la Física tienen su origen en simetrías, y el premio Nobel de Física Philip Warren Anderson ha ido incluso más allá al declarar que «no exagero demasiado si digo que la Física es el estudio de la simetría».
¿Por qué tienen tanta relevancia las simetrías en Física? La HUM da como respuesta que nuestra realidad física tiene propiedades de simetría porque es una estructura matemática, y las estructuras matemáticas tienen propiedades de simetría. La cuestión más profunda de por qué la estructura particular que habitamos tiene tanta simetría se torna equivalente a plantearse por qué nos encontramos en esta estructura particular, y no en otra con menos simetría. Parte de la respuesta quizá radique en que las simetrías parecen ser más la regla que la excepción en las estructuras matemáticas, sobre todo en las grandes que no ocupan puestos demasiado bajos dentro de la lista maestra, donde algoritmos simples definen relaciones para un número enorme de elementos precisamente porque todos ellos tienen propiedades en común. También podría deberse a un efecto de selección antrópica, tal como señaló el propio Wigner, porque es muy probable que la existencia de observadores capaces de detectar regularidades en el mundo que los rodea requiera simetrías, de modo que, dado que somos observadores, sería de esperar que nos halláramos en una estructura matemática altamente simétrica.
Imaginemos que intentáramos encontrarle el sentido a un mundo donde los experimentos nunca fueran repetibles, porque el resultado dependiera del lugar y el instante exactos en el que se realizaran. Si las piedras lanzadas al aire se precipitaran a veces hacia abajo, otras hacia arriba y otras hacia los lados, y el resto de cosas que nos rodean parecieran comportarse también de un modo aleatorio sin ningún patrón o regularidad apreciables, entonces tal vez no habría habido ninguna razón para desarrollar un cerebro. La forma en que suele exponerse la Física moderna trata las simetrías como una entrada y no como una salida. Por ejemplo, Einstein basó la relatividad especial en lo que se denomina simetría de Lorentz (el postulado de que no podemos saber si permanecemos quietos, porque todas las leyes de la Física, incluidas las que rigen la velocidad de la luz, son las mismas para todos los observadores en movimiento uniforme). De manera semejante, una simetría llamada SU(3) × SU(2) × U(1) se considera a menudo como un supuesto de partida para el modelo estándar de la Física de partículas.
Con la hipótesis del Universo matemático se invierte la lógica: las simetrías no son un supuesto, sino tan solo propiedades de la estructura matemática que se pueden calcular a partir de su definición en la lista maestra. Especulativo, pero muy interesante.
El espejismo de las condiciones iniciales
Si se compara con la manera habitual en que se enseña Física, el Multiverso del nivel IV brinda un punto de partida muy diferente para abordar esta disciplina, y eso obliga a reinterpretar la mayoría de los conceptos físicos tradicionales. Como acabamos de ver, algunos conceptos, como las simetrías, conservan su valor crucial. En cambio, otros conceptos, como las condiciones iniciales, la complejidad y la aleatoriedad, se reinterpretan como meras ilusiones existentes tan solo en la mente del observador y no en la realidad física exterior.
Examinemos en primer lugar las condiciones iniciales. Nadie capta la idea tradicional de las condiciones iniciales mejor que Eugene Wigner: «Nuestro conocimiento del mundo físico ha quedado dividido en dos categorías: las condiciones iniciales y las leyes de la naturaleza. El estado del mundo se describe mediante las condiciones iniciales. Estas son complejas y en ellas no se ha descubierto ninguna regularidad exacta. En cierto sentido, a los físicos no les interesan las condiciones iniciales, sino que dejan su estudio a los astrónomos, geólogos, geógrafos, etc.». En otras palabras, lo tradicional en Física ha sido denominar «leyes» a las regularidades conocidas, e ignorar gran parte de lo que no entendemos como «condiciones iniciales». Las leyes permiten predecir cómo cambiarán con el tiempo esas condiciones, pero no aportan ninguna información sobre por qué empezaron del modo en que lo hicieron.
A diferencia de lo anterior, la hipótesis del Universo matemático no deja ningún espacio a semejantes condiciones iniciales arbitrarias, y las elimina por completo como concepto fundamental. Esto se debe a que nuestra realidad física es una estructura matemática completamente especificada en todos los aspectos por su definición matemática dentro de la lista maestra. Cualquier supuesta teoría del todo que afirmara que todo «surgió» o se «creó» sin más en algún estado no especificado en su totalidad, constituiría una descripción incompleta y, por tanto, infringiría la HUM. Una estructura matemática no puede estar indefinida en parte. De modo que la Física tradicional acepta las condiciones iniciales, mientras que la HUM las rechaza.
El espejismo de la aleatoriedad
Esta exigencia de que todo esté definido obliga a la HUM a desterrar otro concepto que ha desempeñado un papel esencial dentro de la Física: la aleatoriedad. Con independencia de que todo pueda parecerle aleatorio a un observador, en última instancia tiene que tratarse de una ilusión, algo que no exista a un nivel fundamental, porque no hay nada aleatorio en una estructura matemática. Sin embargo, los manuales de Física que se guardan en las estanterías de las bibliotecas están llenos de esa palabra: se dice que las medidas cuánticas producen resultados aleatorios, y que el calor de una taza de café se debe al movimiento aleatorio de las moléculas que lo conforman. Una vez más, la Física tradicional acepta algo que la HUM rechaza.
Los rompecabezas de las condiciones iniciales y de la aleatoriedad están relacionados y plantean una cuestión apremiante. De acuerdo con una estimación aproximada, se necesita casi un gúgol (10100) de bits de información para especificar el estado real de cualquier partícula de nuestro Universo en este instante preciso. ¿De dónde sale esa información? La respuesta tradicional implica una combinación de condiciones iniciales y aleatoriedad: se necesitan muchos bits para describir cómo empezó nuestro Universo, puesto que las leyes tradicionales de la Física no lo especifican, y después se precisan bits adicionales para describir el resultado de varios procesos aleatorios ocurridos desde entonces hasta ahora. Pero como la HUM exige que todo esté especificado, y descarta tanto las condiciones iniciales como la aleatoriedad, ¿cómo se justifica toda esta información? Si la estructura matemática es lo bastante simple como para describirla con unas cuantas ecuaciones, a primera vista parece absolutamente imposible. Pero abordemos ahora estas cuestiones.
El espejismo de la complejidad
¿Cuánta información contiene en realidad nuestro Universo? Como hemos comentado, el contenido de información (la complejidad algorítmica) de algo se corresponde con la cantidad de bits de su descripción autocontenida más breve. Para apreciar la sutileza de esto, veamos en primer lugar cuánta información contiene cada uno de los seis patrones que aparecen en la figura 3:
FIGURA 3
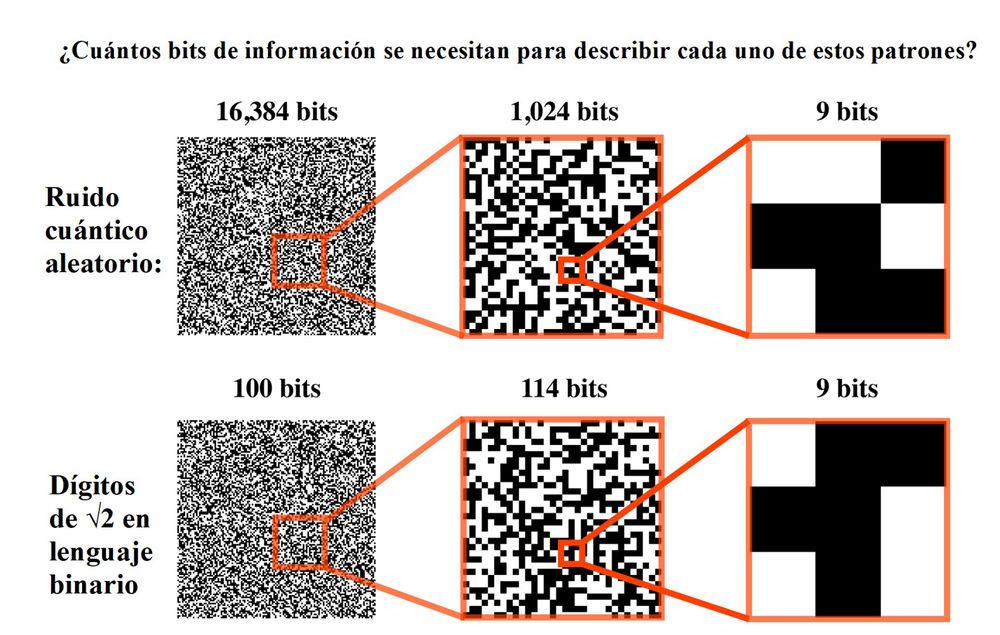
La complejidad de un patrón (cuántos bits de información se necesitan para describirlo) no siempre resulta evidente. El panel de la izquierda superior muestra 128 × 128 = 16 384 cuadrados pintados al azar de blanco y negro, por lo que normalmente no se pueden describir usando menos de 16 384 bits. Los fragmentos más pequeños de este patrón (centro y derecha superiores) consisten en menos cuadros al azar y, por tanto, precisan menos bits para describirlos. El patrón de la izquierda inferior, en cambio, se puede generar mediante un programa muy corto (de 100 bits, por ejemplo), porque no es más que los dígitos de √ (raíz de) 2 en lenguaje binario (0 = cuadro negro, 1 = cuadro blanco). Para describir el patrón del centro inferior se necesitan 14 bits más, para especificar en qué dígito de √ 2 empieza. Por último, el patrón de la derecha inferior requiere 9 bits, igual que el que hay encima de él; el patrón es tan corto que no sirve para nada especificar que forma parte de √ 2.
A primera vista, los dos de la izquierda parecen muy semejantes, como patrones aleatorios de 128 × 128 = 16 384 píxeles minúsculos en blanco y negro. Esto induce a pensar que necesitamos unos16 384 bits para describir cada uno de ellos, un bit para especificar el color de cada píxel. Pero, si bien lo más probable es que ese sea el caso del patrón de la izquierda superior, el patrón que hay debajo de este oculta una simplicidad subyacente: no es más que los dígitos binarios de la raíz cuadrada de dos. Esta sencilla descripción basta para calcular todo el patrón: √ 2 = ≈ 1,414213562…, que en lenguaje binario se escribe como 1,0100001010006110… Digamos, por ejemplo, que este patrón de ceros y unos se puede generar mediante un programa informático de 100 bits de tamaño. Entonces la aparente complejidad del patrón de la izquierda inferior es ilusoria: no tenemos ahí 16 384 bits de información, sino tan solo 100.
Las cosas se vuelven más fascinantes cuando indagamos en la cantidad de información que hay en partes pequeñas de esos patrones. En la fila superior de la figura 3, las cosas son como cabría esperar: patrones más pequeños se tornan más simples y requieren menos información para describirlos: solo se necesita un bit para describir cada pequeño píxel blanco o negro. Pero en la fila inferior, nos encontramos ante un ejemplo justo opuesto. En este caso, menos equivale a más, en el sentido de que el patrón del centro es más complejo que el de la izquierda y precisa más bits para describirlo. Esto se debe a que ya no basta con decir únicamente que se corresponde con los dígitos binarios de √ 2: también hay que especificar en cuál de esos dígitos comienza el patrón, lo que en este caso precisa otros 14 bits de información. En resumen, vemos que el todo puede contener menos información que la suma de sus partes y a veces incluso menos que una de sus partes. Increíble...¿pero cierto?
Por último, cada uno de los dos patrones situados a la derecha en la figura 3 precisa 9 bits para describirlos. Sabemos que el patrón de la derecha inferior se oculta entre los primeros 16 384 dígitos de √ 2, pero este dato deja de ser interesante o útil para un patrón tan pequeño: solo hay 2 9 = 512 patrones posibles con una longitud de 9 bits, de modo que encontrará este patrón particular oculto en la mayoría de las cadenas aparentemente aleatorias formadas por miles de ceros y unos.
Regresemos ahora a nuestro Universo físico y el casi gúgol de bits que parece necesario para especificarlo. Algunos científicos, como Stephen Wolfram y Jürgen Schmidhuber, se han preguntado si gran parte de esa complejidad podría ser también un mero espejismo y derivar de una regla matemática muy simple que aún esté por descubrir. Aunque es una idea elegante, es improbable que todos los números que caracterizan nuestro Universo, desde los patrones en los mapas del fondo cósmico de microondas del WMAP hasta la posición de los granos de arena en una playa, puedan quedar reducidos a casi nada mediante un sencillo algoritmo de compresión de datos. De hecho, la inflación cosmológica predice de manera explícita que las fluctuaciones primordiales cósmicas, las cuales originaron gran parte de esta información en última instancia, se distribuyen como números aleatorios para los que resulta imposible una compresión de datos tan espectacular.
Estas fluctuaciones primordiales especifican todas las maneras en que nuestro Universo primigenio difería de un plasma perfectamente uniforme y fácil de describir. ¿Por qué se muestran tan aleatorios los patrones de las fluctuaciones primordiales cósmicas? De acuerdo con el modelo cosmológico estándar, la inflación genera todos los patrones posibles en distintas partes del espacio (en diferentes Universos de todo el Multiverso del nivel I), y como nosotros nos encontramos en una región muy común de ese Multiverso, veremos un patrón aparentemente aleatorio sin ninguna regularidad oculta que nos ayude a comprimir la información. La situación se parece mucho a la de la hilera inferior de la figura 3, donde nuestro Universo (que se correspondería con el panel de la derecha) equivale tan solo a una pequeña parte de apariencia aleatoria del Multiverso del nivel I (que se correspondería con el panel de la izquierda) y su descripción simple.
La mayoría de los matemáticos cree (aunque aún no se ha demostrado) que los dígitos de √ 2 se comportan como números aleatorios, de modo que en cualquier lugar aparece cualquier patrón posible, igual que los Universos del Multiverso del nivel 1 pueden tener unas condiciones iniciales cualesquiera. Esto significa que una secuencia de un gúgol de dígitos extraída de los dígitos de √ 2 no nos diría nada en absoluto sobre √ 2, sino tan solo acerca de la parte concreta de la secuencia de dígitos que estamos considerando. De igual manera, la observación de cualquier gúgol de bits de información aparentemente aleatorio y extraído de las fluctuaciones cósmicas primordiales generadas por la inflación solo nos revelará hacia qué lugar del vasto espacio posinflacionario estamos mirando.
La complejidad sugiere un Multiverso
Hemos hablado mucho sobre la complejidad de este Universo, pero ¿qué hay de la complejidad de nuestra estructura matemática? La HUM no especifica si la complejidad de la estructura matemática a vista de pájaro es alta o baja, de modo que consideremos ambas posibilidades. Si fuera extremadamente alta, entonces está claro que nuestro empeño por especificarla está condenado al fracaso. En concreto, si para describir la estructura se precisan más bits que para describir el Universo observable, ni siquiera podemos guardar la información referente a la estructura en nuestro Universo; no cabría.
Un ejemplo de teoría con una complejidad así de elevada lo representaría el modelo estándar con sus 32 parámetros especificados explícitamente como números reales, como 1 / α = 1 / 137,035999…, con una cantidad infinita de decimales carentes de patrón simplificador. Con que uno solo de esos parámetros exigiera el almacenamiento de una cantidad infinita de información, la estructura matemática ya tendría una complejidad infinita y sería imposible de especificar en la práctica.
La mayoría de los físicos abriga la esperanza de encontrar una teoría del todo mucho más simple que se pueda especificar mediante una cantidad de bits lo bastante reducida como para caber, si no en una hoja, al menos en un libro, inmensamente inferior al casi un gúgol de bits necesarios para describir nuestro Universo. Esa teoría simple tendrá que predecir un Multiverso, con independencia de si la HUM es cierta o no. ¿Por qué? Pues porque esa teoría será, por definición, una descripción completa de la realidad: si no tiene suficientes bits para especificar por completo este Universo, en lugar de eso tendrá que describir todas las combinaciones posibles de estrellas, granos de arena, etc., de modo que los bits adicionales que describen nuestro Universo sencillamente codifiquen en qué Universo estamos, tal como haría un código postal multiversal.
¿Vivimos dentro de una simulación?
Acabamos de ver que la hipótesis del Universo matemático induce un cambio de perspectiva en muchas cuestiones fundamentales. Centrémonos ahora en otra de ellas: la de las realidades simuladas. Aunque hace tiempo que abunda en la ciencia ficción, la idea de que nuestra realidad exterior es alguna suerte de simulación por ordenador ha cobrado relevancia con películas muy taquilleras, como Matrix. Científicos como Eric Drexler, Ray Kurzweil y Hans Moravec han asegurado que las mentes simuladas son tan posibles como inminentes, y algunos (por ejemplo, Frank Tipler, Nick Bostrom y Jürgen Schmidhuber) han llegado incluso a valorar la probabilidad de que ya haya ocurrido y de que seamos una simulación.
¿Por qué razón pensar que es una simulación? Muchos libros de ciencia ficción han explorado escenarios donde la colonización futura del espacio transforme gran parte de la materia de nuestro Universo en computadoras ultra avanzadas para simular cantidades ingentes de momentos del observador subjetivamente indistinguibles de los nuestros. Nick Bostrom y otros han afirmado que, en ese caso, lo más probable es que su momento actual del observador sea en realidad uno de los simulados, puesto que estos últimos abundan más. Sin embargo, este argumento se autodestruye desde un punto de vista lógico: si el argumento fuera válido, las simulaciones que fueran copias indistinguibles de alguien también podrían construir simulaciones, y eso implicaría que habría muchas más copias que son dobles simulaciones, y que lo más probable sería que ese alguien fuera una simulación dentro de una simulación. Al repetir este argumento, se llega a la conclusión de que lo más probable es que sea una simulación dentro de una simulación dentro de una simulación, y así sucesivamente, hasta alcanzar una cantidad arbitraria de subniveles: "reductio ad absurdum". El error lógico aparece en el primer paso: si se asume que es una simulación, entonces los recursos computacionales de su propio Universo (simulado) son irrelevantes: lo que importa son los recursos computacionales del Universo en el que está ocurriendo la simulación, sobre el cual no se sabe prácticamente nada.
Otros han defendido que a un nivel esencial es imposible que nuestra realidad sea una simulación. Seth Lloyd ha propuesto la posibilidad intermedia de que vivamos en una simulación analógica ejecutada por un ordenador cuántico, aunque no sería diseñado por nadie, porque la estructura de la teoría cuántica de campos es matemáticamente equivalente a la de un ordenador cuántico distribuida por el espacio. En una línea parecida, Konrad Zuse, John Barrow, Jürgen Schmidhuber, Stephen Wolfram y otros han explorado la idea de que las leyes de la Física se correspondan con un cómputo clásico. Analizaremos estas ideas dentro del contexto de la hipótesis del Universo matemático en el siguiente artículo.
CONTINUARÁ..
© 2022 Javier De Lucas