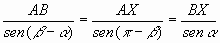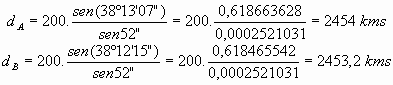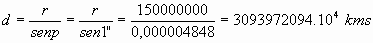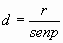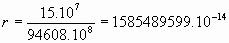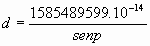La medición de distancias es uno de los problemas arduos de la Astronomía. Si conocemos la magnitud absoluta M, y la magnitud aparente, m, es muy sencillo determinar la distancia en parsecs al astro mediante la conocida relación

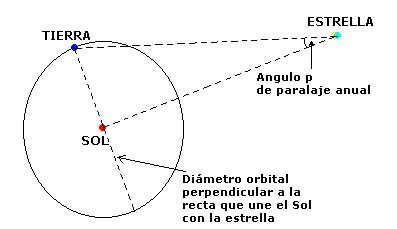
M=m+5-5.log(d)

(se puede despejar log(d), logaritmo decimal de la distancia en parsecs al astro) Cuando a principios del siglo XX se empezó a relacionar la magnitud absoluta estelar con parámetros observables (recordemos el caso de las Cefeidas, de Enrietta Leavitt) se empezaron a medir distancias enormes. Hoy día existen ya sofisticados métodos de medición de distancias en el espacio intergaláctico. Sin embargo, y hasta los comienzos del siglo XX, solo el recurso de la trigonometría permitió medir distancias, nunca de más de 60 o 70 parsecs, por las dificultades que entrañaban la medición de pequeñísimos ángulos (de menos de un segundo de arco). El método del paralaje anual puede ser, en definitiva, efectivo para distancias de unos pocos parsecs.

MEDICIÓN DE DISTANCIAS A OBJETOS INACCESIBLES

La trigonometría elemental nos ofrece procedimientos para calcular la distancia desde un punto dado hasta un objeto al cual no podemos acceder físicamente. Para ello basta efectuar una triangulación, es decir, tomar la referencia de dos puntos hasta los cuales sí podemos acceder y medir los ángulos de visualización del objeto desde ambos puntos a fin de resolver el triángulo correspondiente.

El procedimiento básico consiste en establecer el segmento que definen los dos puntos de observación del objeto, que llamaremos segmento base, y calcular los otros dos lados que representan la distancia desde los puntos extremos del segmento al objeto inaccesible.

Así, si pretendemos calcular la distancia desde el punto A hasta el objeto X, nos movemos a lo largo de una recta arbitraria hasta otro punto B, definiendo el segmento base AB, con lo cual podremos medir el ángulo a que con dicha recta forma una visual al objeto desde A y el ángulo ß que forma con AB otra visual al objeto desde el otro extremo B.

Se tiene entonces que el triángulo ABX puede resolverse elementalmente por conocerse del mismo un lado (distancia AB) y los tres ángulos (a, b, Ya-b).

Y del teorema de los senos, se tiene:

Y puesto que conocemos la longitud AB del segmento base, ya que es accesible para nosotros, tenemos:

Distancia desde A: 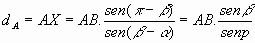Distancia desde B: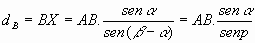

[1]

Donde hemos llamado a-b = p , ángulo que se conoce como la paralaje del objeto X.

Es inmediato que cuanto mayor sea la lejanía del objeto X, más pequeña es la paralaje p =a-b , por lo que, cuando el objeto X, cuya distancia se pretende medir, está demasiado lejano, es conveniente aumentar la longitud del segmento base, a fin de que la medida del ángulo p pueda tener significado.

Ejemplo: Calculemos la distancia a la que se encuentra un objeto sabiendo que hemos medido la distancia rectilínea entre dos puntos A y B, resultando AB=200 kms, y los ángulos del mismo lado que forma la dirección del objeto con el segmento base son 38º12’15” desde A, y 38º13’07” desde el punto B

Usamos las expresiones [1]:

Cuando se toma como segmento base el radio medio de nuestro planeta, la Tierra, se pueden medir distancias de varias unidades astronómicas, dentro de los confines del sistema solar. El ángulo del objeto es la paralaje diurna.

Cuando se trata de medir distancias del orden de años luz es necesario ampliar la longitud del segmento base hasta el radio medio de la órbita de nuestro planeta alrededor del Sol, es decir, de unos 150 millones de kilómetros. Esta es la paralaje anual, que puede resultar útil para medir distancias de hasta unos 250 años luz.

PARALAJE ANUAL. EL PARSEC

- Paralaje anual:

Para hallar las distancias estelares mediante el ángulo de paralaje, hemos de elegir un segmento de base lo suficientemente grande como para medir significativamente dicho ángulo. El mayor segmento que podemos recorrer es el comprendido entre dos posiciones en los extremos de un diámetro de la órbita de nuestro planeta.

Así, cuando utilizamos como segmento base el radio medio de la órbita terrestre alrededor del Sol se dice que estamos calculando las distancias mediante paralaje anual. Para ello, hemos de determinar el diámetro orbital que es perpendicular a la línea que va desde el sol a la estrella:

Figura 1

- El parsec:

Las unidades de medición pueden ser años luz (distancia recorrida por la luz en un año), o bien otra unidad más amplia que se denomina Pársec (conjunción de las palabras paralaje y segundo, ya que se define como la distancia a la cual se encontraría un objeto estelar que tuviera un paralaje anual de un segundo de arco.

- Equivalencia del parsec con el año luz:

Es fácil probar que un parsec corresponde, muy aproximadamente a 3,269 años luz, cálculo que podemos realizar de varias maneras:

a) Si consideramos en la siguiente figura el triángulo rectángulo STE, se tiene que para un radio medio de r=150000000 kms y paralaje p=1”:

Figura 2

La longitud en kilómetros de un pársec podemos determinarla en años luz dividiendo por 300000x60x60x24x365 = 946080000.10⁴, con lo cual:

b) Si consideramos una circunferencia con centro en el objeto estelar que se encuentra a un pársec y determinamos su radio en kilómetros podemos hallar también, muy rápidamente, la equivalencia antedicha de 3,26 años luz:

Figura 3

Esta es la regla de tres:

Si a 1” le corresponden 150000000 kms, entonces a 360º=360x60x60=1296000” le corresponderá la longitud de la circunferencia completa:

Longitud circunferencia = 1,944x10¹⁴ kms, que pasados a años luz dividiendo por el producto 300x60x60x24x365=946080000.10⁴ , nos da: 20,54794521 años luz. Para calcular el radio de esa circunferencia dividiremos por 2p:

DISTANCIAS A LAS ESTRELLAS PROXIMAS MEDIANTE EL MÉTODO DE LA PARALAJE ANUAL

Cuando el objeto cuya distancia se pretende medir está muy lejano el ángulo de paralaje se hace tan pequeño que resulta muy difícil medirlo con alguna precisión.

El método del ángulo de paralaje anual puede resultar útil para las ya mencionadas distancias de no más de 60 o 70 parsecs. Para distancias mayores no es fiable por la dificultad para medir ángulos tan pequeños.

La distancia viene dada por la expresión ya utilizada antes

 

Si r, el radio medio de la orbita de la Tierra alrededor del Sol, viene expresado en años luz, entonces, directamente, la distancia estelar se obtiene en años luz tambien.

Para pasar el radio medio orbital de 15x107 kms a años luz, hemos de dividir por el número 300x60x60x24x365=94608x10⁸, obteniéndose:

 

por tanto, si es p la paralaje anual de la estrella, su distancia en años luz viene dada por la expresión

 

Ejemplos de determinación de algunas distancias estelares

Estrella	Paralaje anual en segundos de arco	Distancia en años luz
Próxima Centauri	0,763	004,29
Sirio	0,374	008,80
61 cyg	0,296	011,00
Procyon	0,291	011,30
Vega	0,130	025,30
Arcturo	0,091	035,93
Capella	0,080	042,20
Aldebarán	0,053	065,00
Dubbe	0,020	138,00
Betelgeuse	0,017	192,00

Conocida la distancia en años luz y la magnitud visual (se determina fotométricamente), la magnitud absoluta de estas estrellas puede establecerse mediante la conocida relación

M = m+5-5.log(p)

(p es la distancia en parsecs y log decimal)

Así, por ejemplo, en los casos de Vega, Capella y Dubbe, de magnitudes visuales

Vega: M =0,03+5-5.log(25,3/3,26)=0,58
Capella: M=0,08+5-5.log(42,2/3,26)=-0,48
Dubbe: M=1,82+5-5.log(138/3,26)=-1,31