UNIVERSO Y PUENTES EPR

La geometría de Schwarzschild constituyó la primera solución exacta a las ecuaciones de Einstein de la Relatividad General. Como es sabido, esta solución representa un agujero negro esférico y estático. Sin embargo, si realizamos un cambio de coordenadas adecuado y utilizamos la métrica Euclidea de esta geometría nos encontramos todo un mundo nuevo y fascinante, un mundo que representa un sistema de dos espacio-tiempos entrelazados. En este artículo nos adentraremos en los secretos más profundos de esta fascinante geometría.

Agujeros negros eternos y puentes de Einstein-Rosen

Las ecuaciones de la relatividad general poseen una simetría denominada "invarianza ante difeomorfismos". Esto básicamente significa que las soluciones a las ecuaciones no cambian si realizamos cualquier cambio de coordenadas. Las repercusiones derivadas de esta simetría son enormes: cualquier sistema de coordenadas y por tanto cualquier sistema de medición de distancias que usemos es equivalente a cualquier otro. Lo único que tenemos que hacer para pasar de un sistema de referencia a otro es adecuar la métrica al nuevo sistema de coordenadas.

La primera solución exacta a las ecuaciones de la relatividad general fue encontrada por el físico Karl Schwarzschild. Esta solución representa un agujero negro esférico y estático (eterno) con la siguiente métrica:

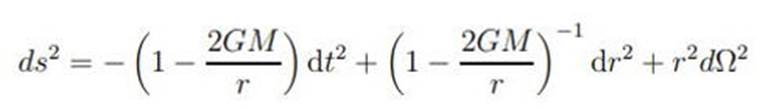
Esta métrica presenta una singularidad en el horizonte para r=2GM. Como las soluciones no cambian al cambiar el sistema de referencia podemos usar cualquier otro sistema de coordenadas. A continuación usaremos el siguiente sistema de coordenadas:

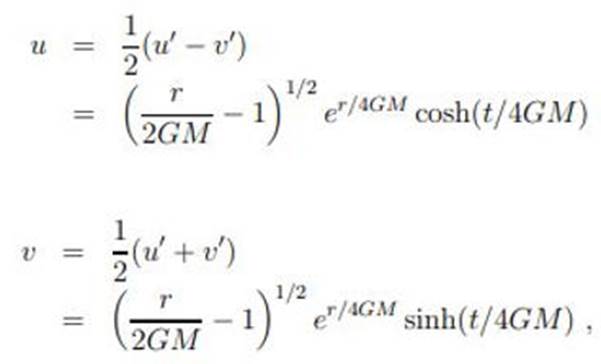
En este nuevo sistema de coordenadas nuestra métrica anterior pasa a ser:

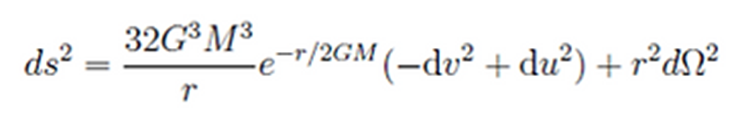
Si calculamos ahora la métrica en el horizonte, en r=2GM encontramos que ¡La singularidad ha desaparecido! Esto nos indica que esta singularidad no es real sino un artificio derivado de la elección de una métrica concreta. Estas nuevas coordenadas se denominan coordenadas de Kruskal y si dibujamos la gráfica dando valores a u y v obtenemos 4 zonas desconectadas separadas por un horizonte de sucesos:

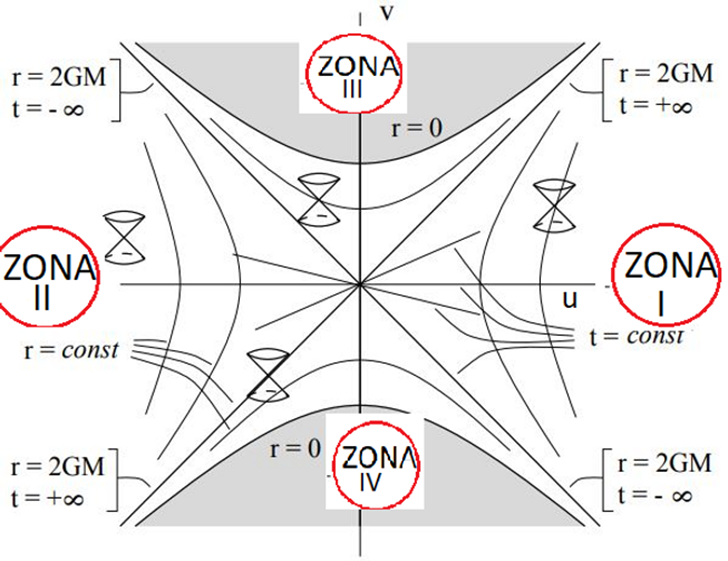
Las zonas I y II representan el exterior del agujero negro mientras que las zonas III y IV representan el interior del agujero negro y poseen una geometría asintóticamente AdS (esto es básicamente la forma de un hiperboloide).

Puesto que estas zonas están desconectadas causalmente, las cuatro zonas pueden interpretarse como un sistema de dos agujeros negros (cada uno con su interior y su exterior) con geometría AdS que no interaccionan entre sí. La zona central del diagrama es una zona común a los dos sistemas de agujeros negros y se denomina "puente de Einstein-Rosen". Este "puente" es la zona de unión de las gargantas de las dos geometrías AdS:

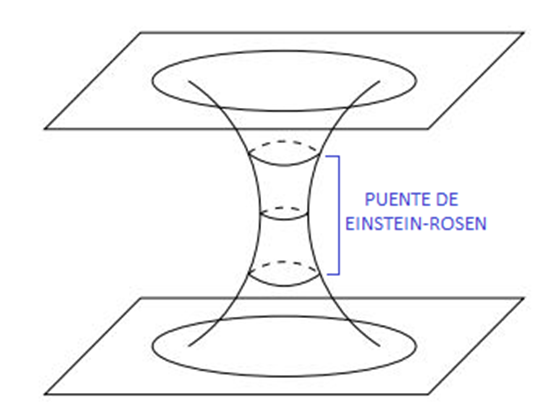
Este "puente" también se denomina "agujero de gusano" y no es transitable ya que se cierra antes de que cualquier señal pueda atravesarlo. Por esto decimos que ambos agujeros negros están causalmente desconectados.

La dirección temporal en la geometría de Kruskal

A continuación analizaremos la coordenada temporal de este agujero negro eterno.

La métrica Euclidea de una métrica Lorentziana como la de Schwarzschild se obtiene permitiendo que la coordenada temporal tome valores complejos. Aunque esto pueda parecer extraño es una técnica bastante extendida denominada "rotación de Wick" y está matemáticamente permitida bajo ciertas condiciones especiales como la que nos ocupa. La métrica Euclidea de un agujero negro en 3D puede escribirse, de forma equivalente, de las siguientes formas:

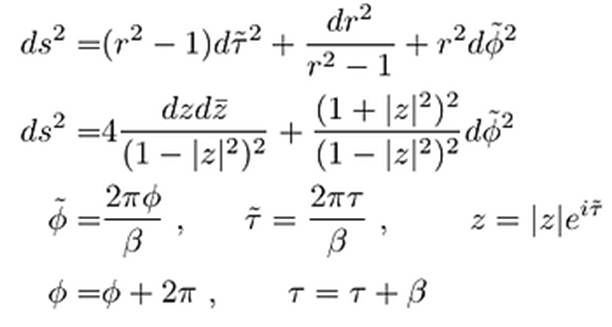
Donde tau y alpha son las coordenadas del borde del espacio AdS y B es la temperatura. Realizando una continuación analítica para z distinto de 0 y haciendo:

z=-v y z=u

obtenemos la métrica de Kruskal en coordenadas Euclideas:

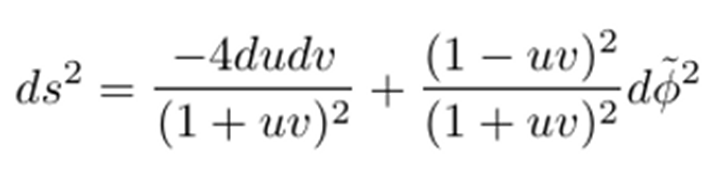
Donde u=t+x y v=t-x. Es ahora cuando llegamos al punto clave: esta métrica no es estática sino que depende del tiempo. La coordenada temporal no varía si realizamos el siguiente cambio:

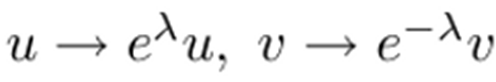
Analizando las trayectorias temporales de esta simetría obtenemos que en la Zona I el tiempo fluye "hacia adelante" (signo positivo), en la II fluye "hacia atrás" (signo negativo) y en las zonas III y IV el tiempo fluye hacia la singularidad. Por tanto, la coordenada temporal tiene una simetría especular respecto al eje t=0 . La siguiente pregunta sería: ¿Qué sucede en el punto t=0? ¿Podemos calcular la métrica en este punto? La respuesta es que sí: si tomamos la métrica Euclidea equivalente a la métrica de Kruskal y analizamos la geometría justo en z=0 obtenemos la siguiente sección:

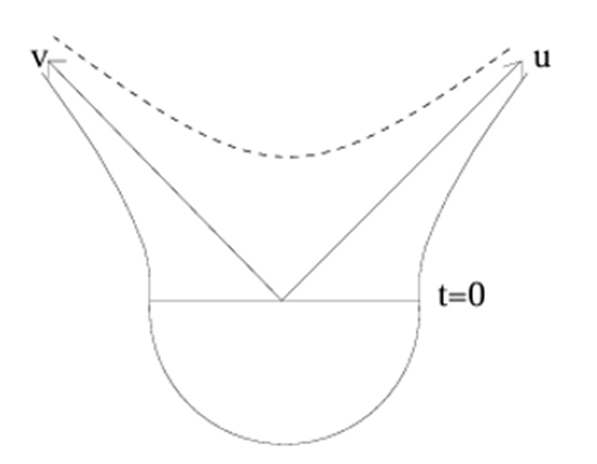
Esta geometría tiene un aspecto bastante familiar: ¡Es la construcción de la función de onda de Hartle-Hawking! En el instante t=0 existe una geometría Euclidea correspondiente al estado de no contorno de Hartle-Hawking. Esta geometría inicial da lugar al Universo Lorentziano usual correspondiente a una mitad del agujero eterno de Kruskal. Si realizamos la misma construcción en la otra mitad y pegamos ambos Universos, en el instante t=0 podemos considerar el punto z=0 como el instante de la creación de dos Universos entrelazados. De esta forma este agujero negro eterno puede interpretarse como un espacio-tiempo con dos Universos entrelazados conectados por un agujero de gusano no transitable producido en el instante de su creación.

La función original de no contorno de Hartle-Hawking implica la creación de un solo Universo donde la energía de la materia es exactamente igual pero de signo opuesto a la energía de la gravedad. Por tanto, la energía total del Universo es cero. Sin embargo, estudios posteriores indican que estas dos energías podrían no cancelarse exactamente. En este caso, la cancelación de la energía total se produciría mediante la creación de dos Universos entrelazados cuya energía total combinada se cancela. El tiempo en ambos Universos fluye en sentido contrario pero un observador en cualquiera de los dos Universos mediría que ambos Universos están o bien expandiéndose o bien contrayéndose.

Radiación de Hawking y la conjetura ER=EPR

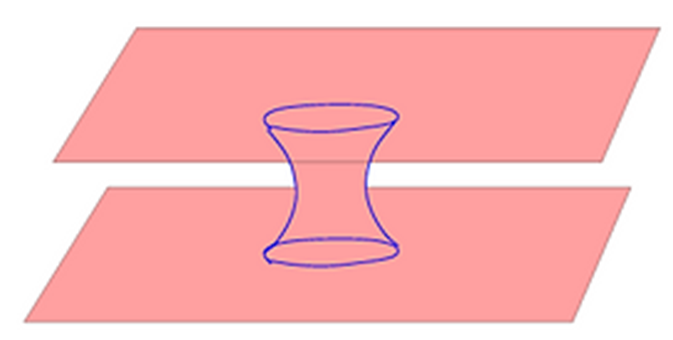
Existen dos posibles interpretaciones del puente de Einstein-Rosen (ER) del agujero negro eterno de Schwarzschild. En la primera interpretación, el puente "conecta" dos geometrías asintóticamente AdS de dos espacio-tiempos diferentes:

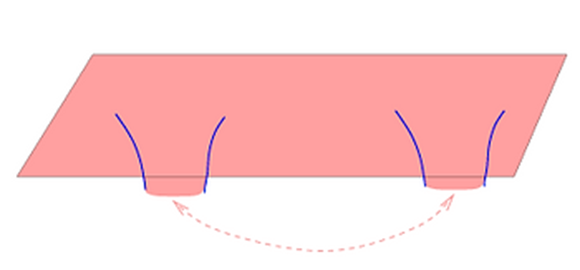
La segunda interpretación implica una "conexión" entre dos geometrías asintóticamente AdS del mismo espacio-tiempo:

Como he recalcado, esta conexión no implica violaciones de la causalidad porque no es posible transmitir información a través del puente. El famoso experimento de Bell implica que si creamos dos partículas entrelazadas y medimos el spin de una de ellas automáticamente sabemos que el spin de la otra partícula deber tener el valor opuesto. Esto se cumple ¡aunque las partículas estén separadas años luz de distancia! Este experimento fue propuesto en primera instancia por los físicos Einstein, Podolsky y Rosen; en honor a ellos este fenómeno se denomina experimento EPR. Si analizamos las propiedades que hemos visto del puente de Einstein-Rosen (ER) y las propiedades del experimento de Einstein-Podolsen-Rosen (EPR) con partículas entrelazadas observamos similitudes asombrosas. Estas similitudes junto con otros indicios teóricos llevaron a Juan Maldacena y Leonard Susskind (dos de los físicos teóricos más importantes de la actualidad) a proponer la conocida conjetura ER=EPR: toda partícula entrelazada está conectada con su compañera a través de un (micro)puente de Einstein-Rosen. Aunque esta conjetura parezca demasiado exótica y especulativa hay indicios teóricos bastante sólidos que parecen respaldarla.

Si esta conjetura es cierta, las partículas de la radiación de Hawking estarían "unidas" con sus partículas compañeras del interior del agujero negro mediante un agujero de gusano:

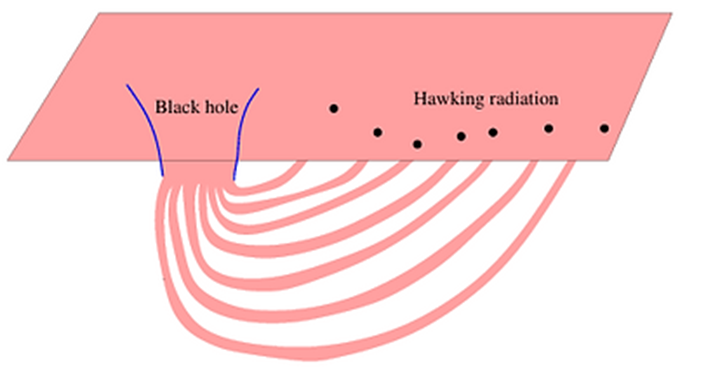
Esto tendría importantes consecuencias en la famosa paradoja de la información de los agujeros negros y apoyaría los recientes descubrimientos que indican que los agujeros de gusano son los responsables de que la información escape del agujero negro.

Para finalizar, en el siguiente apartado descubriremos un fenómeno increíble: aunque no es posible enviar señales a través del puente de ER sí podemos conectar el interior de ambos agujeros negros. En realidad sería posible establecer una comunicación, pero esta información no puede ser vista por el resto del Universo: la información estará oculta para siempre dentro del agujero negro.

Conectando el interior de dos agujeros negros eternos

Supongamos que creamos un conjunto de N partículas entrelazadas, las separamos varios años luz de distancia y las colapsamos para formar dos miniagujeros negros. Siguiendo los principios de la mecánica cuántica y de la relatividad general estos dos agujeros negros estarán entrelazados.

Imaginemos que en algún lugar de nuestro inmenso Universo una civilización muy avanzada consigue alcanzar la tecnología necesaria para comprimir la materia hasta alcanzar el radio de Schwarzschild, siendo así capaces de fabricar agujeros negros macroscópicos. Supongamos que esta civilización fabrica un par de agujeros negros idénticos en el interior de un campo magnético muy intenso. Estudios teóricos precisos de este fenómeno indican estos dos agujeros negros estarán entrelazados.

A continuación un astronauta llamado Bob transporta, en un cohete ultra-rápido, uno de los agujeros negros hasta una región situada a 50 años luz de distancia. Cuando llega a su destino, Bob quiere comunicarse con Alice, que se ha quedado en la Tierra, pero cada mensaje enviado desde su posición tardará 50 años en llegar hasta la Tierra lo que supone una espera inasumible. Entonces a Bob se le ocurre algo sorprendente: si ambos saltan dentro del agujero negro podrán encontrarse dentro y comunicarse. Esto es debido a que el interior de ambos agujeros negros entrelazados es común a ambas regiones exteriores y es accesible causalmente desde el exterior como puede verse en el diagrama conforme de Penrose:

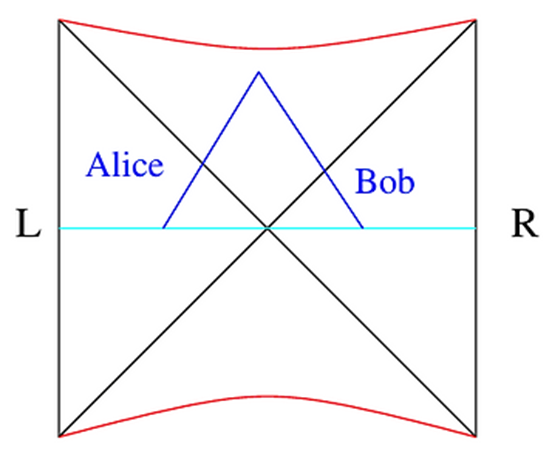
Si Alice y Bob saltan a la vez una vez formado el agujero negro, ambos podrán encontrarse en el interior

Sin embargo, ambos deben saltar dentro de sus respectivos agujeros negros poco después de formarse el mismo; si esperan demasiado ambos llegarán a la singularidad antes de encontrarse:

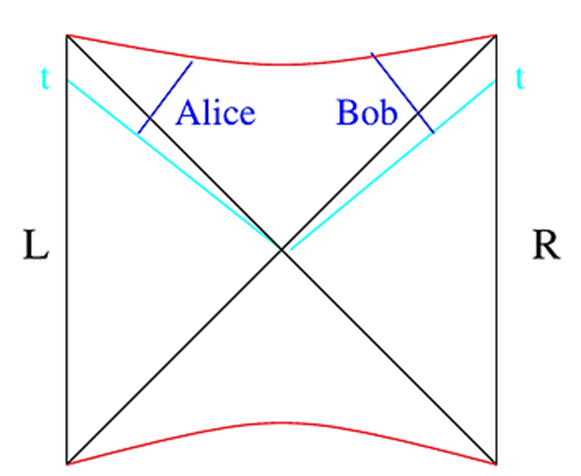
Si ambos esperan demasiado, una vez iniciado el tiempo de formación del agujero ya no será posible el encuentro, ya que antes chocarán contra la singularidad

Este increíble fenómeno parece apoyar el famoso trabajo del físico Raamsdonk en el que se describe cómo el entrelazamiento conecta el propio espacio-tiempo: si aumentamos el entrelazamiento entre dos regiones, el espacio-tiempo entre ellas se acerca, si lo disminuimos, el espacio-tiempo se separa hasta llegar a quedar completamente desconectado.

Por supuesto, no es muy recomendable realizar este experimento, ya que nadie podrá saber jamás de que han hablado ambos astronautas dentro del agujero negro y al final la singularidad marcará el trágico destino de todo aquel que se interne en el agujero.