QUIMICA DEL CAOS

QUIMICA DEL CAOS

La reacción de Bray

EN 1921, W. C. Bray, investigador de la Universidad de California, realizaba un estudio sobre la transformación del agua oxigenada catalizada por diversas sustancias. En particular, el trabajo consistía en evaluar la eficiencia del yodo para promover la mencionada reacción. Recordemos que un catalizador es una sustancia que acelera la velocidad de una transformación química, y que permanece inalterado al final de la misma. Además de ser eficiente para convertir el mayor número de moléculas-reactivo por unidad de tiempo, un catalizador debe poseer otra propiedad muy preciada: la de ser selectivo, es decir, que ante la posibilidad de llevar a cabo la conversión por diferentes rutas, escoge preferentemente una de ellas, lo que orienta la reacción hacia determinado tipo de productos. En presencia de yodo como catalizador, el agua oxigenada se descompone en productos de acuerdo con la siguiente reacción global:

10 H2O2 =10 H2O + 5 O2

Es decir, por cada diez moléculas del reactivo se generan otras tantas de agua y adicionalmente cinco de oxígeno. Mediante un dispositivo experimental sencillo, Bray siguió el curso de la reacción en función del tiempo, midiendo la cantidad de yodo que se desprendía de su sistema.

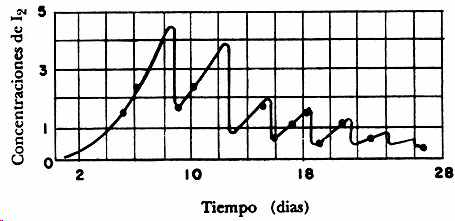
La figura nos muestra los resultados de tal ejercicio; el eje vertical representa la concentración de yodo y el horizontal el tiempo, expresado en días. Para asombro de Bray, el proceso seguía un modelo oscilatorio en el cual el yodo aumentaba y disminuía durante la transformación, algo poco usual para una reacción química en aquella época, cuando se esperaría que el trazo que une los diferentes puntos fuese una línea continua. Bray no se amilanó ante las posibles críticas y publicó sus resultados ese mismo año en una prestigiada revista científica, sin que nadie se interesara en ellos. Un par de años después aparecieron dos o tres artículos que daban una explicación «científica» de los hechos: lo que provocaba esas artificiosas oscilaciones seguramente se debía a la falta de precaución de Bray en emplear un reactivo «obviamente» contaminado, o bien, según otros, ¡había partículas de polvo en el medio de reacción!

Más de cincuenta años durmió el sueño de los justos la famosa reacción de Bray. Cuando se repitieron los experimentos, que obviamente reprodujeron el modelo oscilatorio, se consideraron como bichos raros dignos de ejecutarse en las prácticas de química en las universidades, para diversión de los estudiantes. ¿Por qué la apatía de los químicos ante los resultados de Bray? En otras áreas de la ciencia, como el caso de la biología, la astronomía o la física, por nombrar algunas, los científicos están acostumbrados a las oscilaciones; pero en la química, quien se atrevía a mencionar las oscilaciones recibía categórica respuesta: «Si eso fuese cierto se estaría violando el segundo principio de la termodinámica, más aún, mi querido colega, eso es el equivalente a diseñar una máquina de movimiento perpetuo.». Antes de opinar sobre la cordura de nuestro científico, veamos primero qué nos dicen los mencionados principios termodinámicos.

La termodinámica

La primera ley de la termodinámica afirma la conservación de la energía para todos los sistemas. El incremento de energía en el seno de un sistema es igual a la cantidad de energía que ha recibido. Un sistema macroscópico puede estar constituido por gran número de componentes y separado del mundo exterior por una superficie geométrica ficticia, de manera que el número total de componentes por volumen es constante. Así, por ejemplo, una célula puede considerarse como un sistema que está compuesto por unas diez mil moléculas. En un sistema aislado no hay intercambio de materia o energía con el mundo exterior. Un sistema cerrado únicamente intercambia energía con el medio externo. Por último, un sistema abierto es aquél que intercambia energía y materia con el mundo exterior. La Tierra, en su conjunto, es un sistema cerrado que recibe energía de los rayos solares (despreciando los intercambios másicos que provienen de la caída de meteoritos, por ejemplo). Por el contrario, una célula de una bacteria es un sistema abierto.

Cuando dos objetos están en contacto y a la misma temperatura, nunca sucederá que uno de ellos se caliente mientras el otro se enfría. Entonces, si bien la energía no se produce ni se destruye, parece fluir únicamente en una dirección. El segundo principio introduce una nueva función de un sistema, la entropía, que está relacionada con los intercambios de calor con el mundo exterior. Contrariamente a lo que sucede con la energía, la entropía no se conserva. Siempre que algún proceso natural genera energía, parte de ella no se convierte en formas utilizables. Está ahí, pero no puede ser empleada, es inalcanzable. La cantidad de energía no utilizable es equivalente al aumento de entropía, que es función creciente de la temperatura. Por ejemplo, considérese que a baja temperatura el estado sólido está constituido por un sistema que tiene una estructura ordenada, mientras que si la temperatura es lo suficientemente elevada se presenta el estado gaseoso, de entropía mayor y estructura desordenada. Para un sistema cerrado homogéneo que se encuentra a temperatura y presión constantes, un cambio químico espontáneo debe, sin duda, estar acompañado de una disminución en la energía disponible o, si se quiere ver de otra manera, por un aumento en la entropía. Por lo tanto, el conjunto tiende hacia un estado permanente e inequívoco, que es el equilibrio termodinámico. Por el contrario, cuando el sistema es abierto puede tender hacia un régimen constante, que no es el del equilibrio, llamado estado estacionario. El escepticismo de los químicos de la época ante los resultados de Bray se debía en parte a que pensaban que si la energía libre del sistema disminuía en forma continua, esto debía reflejarse en un aumento o disminución correspondientes de las concentraciones de las especies químicas presentes durante la transformación, es decir, la conversión de A en B debería ser continua, sin que en un momento B regresara para formar A nuevamente.

A partir de los años cincuenta se realizó una revisión de los conceptos termodinámicos y entre el grupo de científicos que trabajaron en ello destaca la labor de Ilya Prigogine, químico ruso emigrado a Bélgica. Prigogine aportó las bases teóricas para describir el comportamiento de los sistemas físicos que se encuentran alejados del equilibrio termodinámico, trabajo que le valió ser galardonado con el premio Nobel de Química en 1967. Lo que podemos resumir de estos estudios es que en un sistema bajo esas condiciones se pierde la homogeneidad espacial y temporal que prevalece cerca del equilibrio. Ante esas circunstancias es posible que se presenten oscilaciones en una reacción química, aunque los productos al inicio y al final no estén sujetos a ellas. Un sistema alejado del equilibrio tiene, como veremos, un comportamiento impredecible, caótico para ser claros, pero en esas condiciones el desorden máximo deja de ser la regla y nada prohíbe también la emergencia de un orden temporal o espacial.

Las células de Bénard son un ejemplo del orden espacial en el cual el sistema, de estar en el equilibrio, debería presentar una temperatura uniforme en el recipiente, pero sucede que cuando la diferencia de temperatura alcanza cierto valor, aparecen continuamente pequeñas corrientes de convección, como pulsos que regresan a su estado inicial, y a partir de un punto crítico ciertas pulsaciones se amplifican y dan lugar al movimiento macroscópico que origina la estructura ordenada en forma de células hexagonales.

El movimiento de las reacciones

¿Cómo se representa la evolución temporal de una reacción química? En un principio, la química estudió las propiedades de las sustancias, luego las de su composición, pasó después a las leyes que determinan las propiedades y estructuras, hasta finalmente llegar al estudio de las leyes de la transformación química. Podemos decir, en términos generales, que primero existió la química descriptiva, luego la estructural seguida de la termodinámica, para llegar por último a la química cinética, es decir, el estudio de las velocidades de reacción. La química descriptiva y la estructural se especializan en el estado de la materia, la «fotografían»; mientras la termodinámica considera los cambios de la materia, estado a estado, o sea, «compara las fotografías», la cinética estudia el paso de un estado al otro, «filma» el evento. La cinética toma en consideración el camino que sigue la transformación, y la velocidad de una reacción depende obviamente del camino que sigue.

La interpretación cuantitativa de los resultados de una reacción química se basa en la construcción y análisis subsecuente de un modelo por el cual los reactivos llegan a los productos finales, y especifica, si es posible, todas las especies intermediarias que intervienen. Así, por ejemplo, en el caso de la reacción de Bray la velocidad de la desaparición del agua oxigenada se puede definir como:

v = k (A)

en donde v representa la velocidad de desaparición del reactivo, expresada por ejemplo en número de gramos por unidad de tiempo, k es una constante que depende de la temperatura y (A) representa la concentración del reactivo en un tiempo dado. Suele suceder que el mecanismo o modelo por el cual la reacción pasa del reactivo inicial a los productos sea más complejo que como lo describimos con anterioridad. Por lo común, la molécula de agua oxigenada no genera directamente en un solo paso los productos de reacción, sino que en el curso de la transformación aparecen y desaparecen especies intermedias de vida muy corta que pueden ser detectadas con los dispositivos de medición que utilicemos.

La ecuación anterior sólo nos describe la velocidad de transformación global que se deriva de combinar todas las reacciones intermedias que son teóricamente posibles. Si analizamos un poco más a fondo la reacción de Bray, encontraremos que suceden unas transformaciones intermedias que sumadas equivalen a:

10 H2O2 + I2 + 2 HIO3 → 5O2 + 2 HIO3 + I2 + 10 H2O

Al hacer la resta entre los componentes comunes a ambos lados de la ecuación, llegamos a la ecuación original que habíamos descrito anteriormente. En nuestro conocido diagrama de fases podemos describir la dinámica de un sistema mediante un esquema, el que se representa en la figura para una reacción teórica en la que un compuesto A reacciona con otro B para dar un producto final.

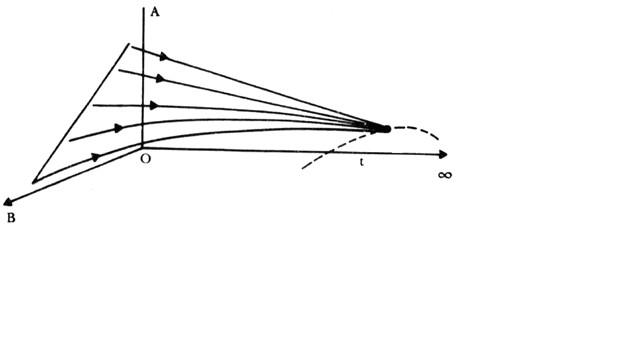
En el diagrama se muestra cada una de las masas de los dos reactivos y el tercer eje representa el tiempo. Los reactivos parten de cierta concentración inicial y evolucionan hasta alcanzar un equilibrio en el cual su concentración ya no cambia en el tiempo. Como podemos observar, en este esquema sencillo existe un atractor de punto fijo.

Lotka y las oscilaciones

¿Cómo explicar desde el punto de vista cinético una reacción oscilatoria? Existía un modelo teórico que daba cuenta de este tipo de comportamiento y había sido descrito por Alfred Lotka en 1920 para explicar las oscilaciones que suceden en problemas de tipo ecológico. El mecanismo propuesto consiste en tres «reacciones», de las cuales dos de ellas son autocatalíticas:

(P)+ C = 2C

C + L = 2L

L =

Aquí (P) representa el pasto del cual se alimentan los conejos, es decir, C. Dado que el pasto está en una concentración muy elevada podemos tomarlo como un valor constante que no interviene en el mecanismo. Al alimentarse de pasto los conejos se reproducen, lo cual representa la primera reacción autocatalítica dado que los conejos aceleran su propia creación. La segunda reacción autocatalítica la representan los lobos, L, que crecen y se reproducen a expensas de los conejos, con lo cual la población de conejos disminuye. Eventualmente los lobos mueren, y los conejos vuelven a elevar su población.

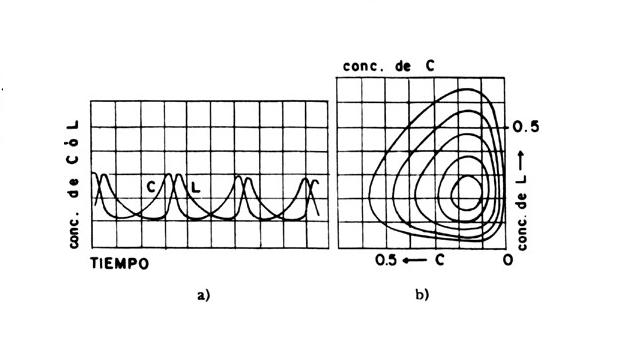
En la figura se presenta una solución a este ciclo, utilizando un conjunto de tres ecuaciones diferenciales que se realizaron en ordenadora. En la figura (a) se muestra la concentración de C o de L en función del tiempo y en la figura (b), la concentración de uno en función del otro. En este último caso lo que se obtiene es una curva cerrada, casi una elipse; por tanto, conforme el sistema sigue la curva, las concentraciones de C o L varían de una manera periódica.

Hasta principios de los años sesenta los químicos no conocían un sistema real que se comportara de acuerdo con el esquema de Lotka; obviamente la reacción de Bray había sido olvidada pero los estudios de Prigogine demostraban que dicho tipo de oscilaciones eran posibles. La evidencia experimental que faltaba la había realizado B. P. Belousov en 1958, un químico ruso.

La extraña reacción que descubrió Belousov

En 1959 B. P. Belousov; biofísico que trabajaba en el Ministerio de Salud de su país, en un congreso de medicina informó de un dato peculiar que había observado en el curso de una reacción química que estaba estudiando. Como en el caso de la reacción de Bray, este dato fue olvidado durante algún tiempo hasta que los trabajos de Prigogine se dieron a conocer.

La historia es sencilla: el científico estudiaba en su laboratorio una reacción de oxidación de un compuesto orgánico, el ácido cítrico, el cual se trata con una sal de bromo y la conversión se cataliza por acción de una sal de cerio que sirve para aumentar la velocidad de la transformación. El cerio en solución acuosa inicialmente tiñe el líquido de color amarillo y una vez que cataliza la reacción se vuelve incoloro. Como es de esperarse en una reacción clásica, una vez que se lleva a cabo la transformación, la solución originalmente amarilla debía quedar incolora. Para asombro de Belousov, la solución perdía la coloración amarilla, mas para recobrarla al poco rato, y dichas oscilaciones se observaban por mucho tiempo; o sea que el cerio que se había transformado volvía al punto de partida.

Años más tarde, otro biofísico ruso, A. M. Shabotinsky se interesó en esta curiosa reacción y la estudió más sistemáticamente, realizando varias modificaciones al sistema: cambió el ácido cítrico por el ácido malónico y añadió un compuesto de hierro que permitía observar en forma más clara las etapas de oxidación y reducción que se llevaban a cabo.

La reeacción B-Z

Resumamos los ingredientes de la reacción, ahora conocida como reacción de Belousov-Shabotinsky:

ácido malónico,

ácido inorgánico, que puede ser el sulfúrico,

una sal que aporte iones bromato (BrO3–),

una sal que aporte iones bromuro (Br–),

una sal de hierro (Fe ++),

una solución acuosa.

Precisemos que un ion es un átomo o grupo de átomos cargados eléctricamente y que sus cargas son el resultado de la ganancia o pérdida de uno o más electrones. Cuando un ion se oxida pierde electrones y cuando se reduce los gana. Así, los iones de hierro en el estado reducido (Fe ++) dan una coloración roja, y al oxidarse se convierten en Fe +++, de coloración azul. Obviamente, una sustancia que se reduce trae aparejado el hecho de que otra se oxide. Las modificaciones que hizo Shabotinsky en la reacción permitieron observar que además de las oscilaciones temporales se presentaban estructuras espaciales en el seno de la reacción inicialmente homogénea, las cuales se prolongaban durante mucho tiempo.

Si se espera el tiempo suficiente para que se alcance el equilibrio dictado por las leyes de la termodinámica, lo que se encontrará en el recipiente es bióxido de carbono, agua y el ion bromuro. Pero las curiosas oscilaciones no son el producto de la reacción global, sino de las transformaciones intermedias que ocurren. Cuando la reacción se realiza en una caja cilíndrica a temperatura ambiente, en el inicio es roja; súbitamente, parte de esta solución se vuelve azul y comienza a diseminarse por toda la caja, formando un disco. Dado que la reacción es oscilatoria, el centro del disco azul vuelve a ser rojo otra vez y éste se convierte en un anillo.

Conforme las oscilaciones continúan, el centro del anillo torna otra vez al color azul, lo cual formará otra vez un disco que se convertirá en anillo. Se tiene por lo tanto un modelo de anillos concéntricos que se propagan. Las ondas de color representan las variaciones en la concentración de especies químicas que se propagan en un sistema inicialmente homogéneo. Es decir, estamos en presencia de una inestabilidad como la de Bénard, salvo que en este caso las oscilaciones son espaciales y temporales a la vez. Algunos autores afirman que las ondas se propagan con velocidades de 6 mm/minuto y emergen a intervalos más o menos iguales de veinte lugares distintos de la caja cilíndrica que en su mayoría no son puntos, sino arcos de curvas de hasta 15 mm de largo.

¿Qué sucede en la reacción B-Z?

¿Cuál es el mecanismo que se ha propuesto para esta reacción? Armar el rompecabezas de esta reacción no ha sido tarea fácil; para ello han intervenido cientos de investigadores en el mundo, quienes aportaron datos cuantitativos sobre las diferentes etapas elementales de la misma. De este trabajo monumental hoy en día se ha establecido una secuencia ni más ni menos que de 18 reacciones elementales, en las que intervienen 21 especies químicas diferentes, las cuales se presentan en la figura.

Tratemos de dar una descripción cualitativa de este fenómeno, para esto nos apoyaremos en la siguiente figura, en la cual sólo se describe parte de las reacciones que intervienen utilizando en este caso al cerio (Ce) como catalizador en lugar del hierro.

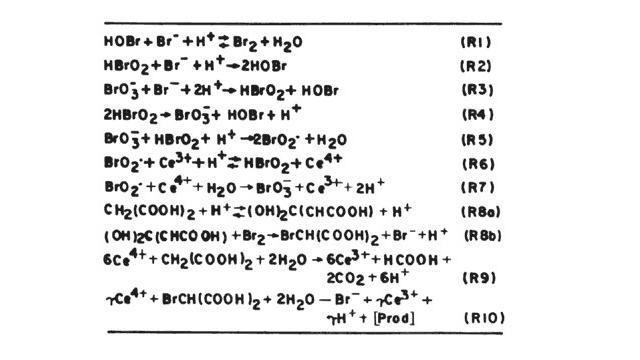
Si recordamos el diagrama de Lotka, una característica del sistema era que existía una reacción autocatalítica, es decir, que una sustancia acelera su propia creación. En la reacción de B-Z existe tal tipo de fenómeno: la especie HBrO2 se genera en R5 y aumenta su cantidad en R6. El HBrO2 se consume en la R2 y en la R5 y cuando la primera reacción domina sobre la segunda, la producción autocatalítica se apaga y las reacciones que predominan son R1, R2, R3, R8a y R8b, que consumen la especie Br– que hacía que R2 fuese predominante sobre R5. Al dejar de predominar se «enciende» el sistema R5 y el R6, que oxidan al catalizador Ce+3 a Ce+4 y se produce el cambio de coloración de la solución. Cuando las reacciones R5 y R6 están funcionando promueven las reacciones R9 y R10; esta última dará los productos finales de la reacción, pero a su vez genera nuevamente Br–, que vuelve a hacer que R2 domine a R5 y recomience el ciclo.

Es obvio que en un sistema cerrado en el cual no se alimentan reactivos la reacción tenderá a un equilibrio al irse consumiendo el ácido malónico y el ácido bromomalónico, que se convierten en bióxido de carbono. Por lo tanto, el siguiente paso era alejar la reacción del equilibrio termodinámico y estudiar en forma más cuantitativa la evolución de las especies intermedias, dejando a un lado los cambios de coloración.

De la oscilación al caos

La estrategia para alejar la reacción del equilibrio consiste en realizarla en un sistema abierto, es decir, en el que se intercambia materia y energía con el medio circundante. Para ello es necesario modificar el sistema de reacción, para lo cual se alimentará en forma independiente y controlada los reactivos, que llegan a un dispositivo en el cual se mezclan y reaccionan, mientras que paulatinamente se extraen los productos de la transformación. La alimentación continua de reactivos y la extracción simultánea de la mezcla de reacción impiden que el sistema alcance el equilibrio. Además, al alimentar los reactivos en forma independiente es posible modificar las concentraciones individuales de cada uno de los participantes y también, si se varía la velocidad de alimentación al reactor, se altera en forma controlada el tiempo en el cual los reactivos están en contacto entre sí, lo que en el argot de los químicos se suele llamar el tiempo de residencia o de contacto.

El análisis cuantitativo de lo que sucede en el reactor se lleva a cabo introduciendo diminutos electrodos sensibles a la variación de las concentraciones de las especies de cerio en sus estados oxidado y reducido, así como otros que son sensibles a la concentración del ion bromuro. Mediante esta metodología experimental, muy elaborada en su aplicación, es fácil que el lector vea que desde el punto de vista de la reacción química, es posible realizar algo equivalente a lo hecho con la ecuación logística, ya que mediante experimentos con diversas condiciones iniciales, como en el curso de reacción, se obtienen datos sobre la dinámica del sistema.

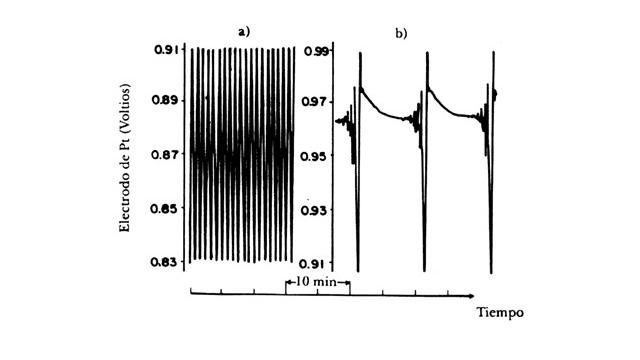
En la figura presento algunos resultados experimentales que se obtuvieron al variar el tiempo de residencia; con un electrodo de platino se midió en forma continua el cambio en el potencial de óxido-reducción de la reacción y con ello se obtuvo una estimación de la relación de iones cerio (III) / (IV). Por lo tanto, en la figura se muestra en el eje horizontal el tiempo de reacción y en el vertical el valor del potencial medido con el electrodo: en el caso de la figura a), el flujo total de reactivos es de un mililitro por minuto, en el caso b) es de 4.0. Figura 26. Oscilaciones de la reacción B-Z en función del flujo de reactivos, a) 1 ml/minuto; b) 4.0.

De los resultados experimentales es evidente que para unas condiciones se presentan oscilaciones regulares, mientras que en otras las oscilaciones son mucho más complejas. Los autores de este trabajo, K Graziani, J.Hudson y R. Schmitz de la Universidad de Illinois, EUA, no dudaron de calificarlos como estados caóticos en una publicación aparecida en 1977. Todavía en 1985 muchos científicos dudaban de los resultados experimentales que se habían acumulado en diversos laboratorios en el mundo: «el hecho de que existan sistemas experimentales que exhiban un comportamiento caótico no prueba que el caos es inherente al mecanismo de la reacción, lo más probable es que se deba a fluctuaciones estocásticas, imposibles de evitar», decían algunos, mientras que otros apuntaban que «todavía es una incógnita la demostración experimental del caos en un sistema químico homogéneo, más bien lo que ha sucedido es que los resultados son el producto de un control imperfecto de los fenómenos externos».

Para vencer el escepticismo de muchos científicos fue necesario realizar exhaustivas pruebas experimentales en las que se amplió el espectro de valores obtenidos modificando tanto los tiempos de residencia como las concentraciones iniciales de reactivos, datos que fueron alimentados a programas computacionales que utilizaban herramientas matemáticas cada vez más complejas. Al mismo tiempo aparecieron informes de otros sistemas que presentaban dinámicas oscilatorias, por lo que se llegó a un punto en que era innegable la existencia de oscilaciones en sistemas aparentemente muy sencillos. ¿El aparente caos en la reacción no sería consecuencia, por ejemplo, de la suma de periodos oscilatorios diferentes en el sistema?

La experimentación y simulación computacional demostró que el caos determinista estaba presente en la reacción de Belousov-Shabotinsky, los argumentos fueron los siguientes: se había demostrado la extrema sensibilidad del comportamiento de la reacción a las condiciones iniciales. Pequeñas modificaciones en las mismas hacían oscilar la reacción con periodos diferentes. Se demostró, por otra parte, la presencia de duplicaciones periódicas, así como de intermitencia del tipo I que, como recordamos en la ecuación logística, son rutas hacia el caos. Además, Graziani y colaboradores demostraron más adelante que bajo ciertas condiciones de reacción, las oscilaciones se ven interrumpidas abruptamente y la reacción entra en un estado no oscilatorio. Por último, una prueba adicional de la presencia del caos resultó cuando se comprobó la existencia de un atractor extraño.

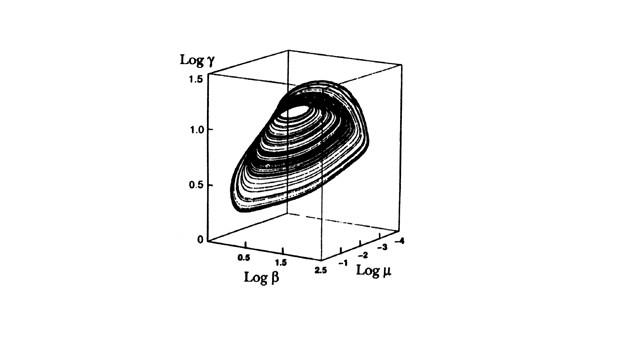
En la figura se muestra la simulación que se obtuvo por ordenador a partir de datos experimentales, empleando el esquema reaccional antes mencionado. La figura no es otra cosa que nuestro conocido diagrama de fases y en él se muestran los valores en escala logarítmica de tres de los componentes del sistema: el ácido bromomalónico (γ) el ion cerio-IV (β) y el ion bromuro (µ). Si el sistema tuviese un comportamiento periódico, sería de esperar que el atractor generado fuese de ciclo limitado, pero éste no es el caso.