RUPTURA DEL ESPACIO-TIEMPO

La teoría definitiva de gravedad cuántica cambiará para siempre nuestra concepción del espacio-tiempo y del Universo que habitamos. Uno de los conceptos clave de este cambio de paradigma podría ser que el espacio-tiempo es en realidad una superposición de geometrías. Si nos basamos en la teoría de la cuantización canónica de la gravedad podemos definir una función de onda del Universo que contiene toda la información sobre la geometría del espacio-tiempo.

En este capítulo veremos algo realmente sorprendente: si esta visión es correcta el espacio-tiempo clásico que conocemos solo está definido en ciertas regiones del superespacio (el espacio de configuraciones donde se define la función de onda del Universo), de hecho, este espacio-tiempo clásico podría romperse a escalas mucho más bajas que la escala de Planck. La "rotura" del espacio-tiempo clásico constituiría el final de la geometría tal y como la conocemos y representaría una región donde el espacio-tiempo clásico es reemplazado por fluctuaciones cuánticas y espacios de probabilidades puramente cuánticos. Esta región puede considerarse un estado más allá del espacio y el tiempo.  

La función de onda del Universo y la "ruptura" del espacio-tiempo 

La formulación canónica de gravedad cuántica está basada en la denominada ecuación de Wheeler-deWitt: 

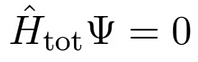
 Donde la función de onda psi es la función de onda del Universo. Una de las soluciones más conocidas a dicha ecuación la constituye la famosa función de onda de no contorno de Hartle-Hawking. En este artículo nos basaremos en esta solución. El espacio-tiempo clásico surge cuando la fase de la función de onda oscila muy rápidamente de forma que las amplitudes correspondientes al resto de geometrías se cancelan y solo se mantiene la geometría clásica. En este caso la función de onda puede ser definida aproximadamente como una suma de términos de la forma: 

 Donde la fase S debe variar mucho más rápidamente que la amplitud A, es decir: 

 En el caso de la función de onda de no contorno la función de onda es aproximada por la suma: 

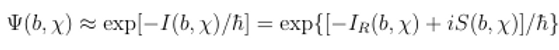
Donde b es el factor de escala del Universo y x es el campo escalar.

Si nos fijamos en la figura del famoso instantón que origina la función de onda de no contorno (ver imagen inferior) el radio de la 4 esfera Euclidea (zona morada) determina Ir mientras que el régimen Lorentziano (zona verde) determina S: 

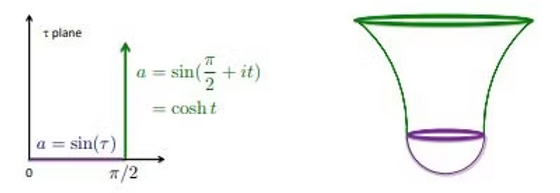
 Por tanto, la variación de la amplitud Ir respecto de la fase S viene dada por:

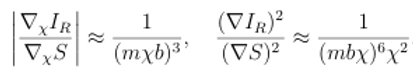
La condición para un espacio-tiempo clásico será:

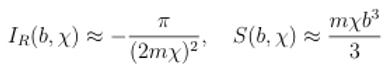
Por tanto la condición para una geometría clásica es:

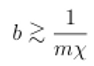
Este es el primer punto clave del artículo: es sabido que el espacio-tiempo clásico se rompe cerca de la escala de Planck, esto es, cuando la energía potencial del escalar x

alcanza la escala de Planck. Esto sucede para x=1/m, es decir cuando V=1 (en unidades de Planck). Sin embargo, la expresión anterior nos dice que la geometría clásica se rompe cuando b=1/mx esto es, mucho antes de la escala de Planck.  

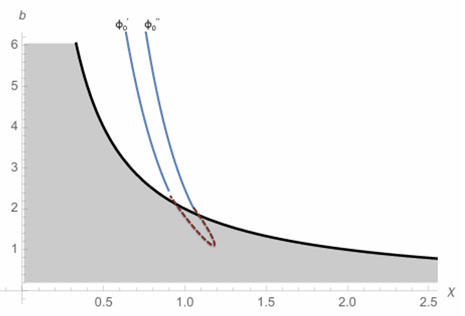
 La gráfica nos muestra que para los valores de b y x en el intervalo punteado las trayectorias psi_o´ y psi_o´´dejan de ser clásicas y el espacio-tiempo se comporta de forma puramente cuántica. La zona sombreada es una región donde el espacio-tiempo clásico que conocemos no existe. Esta zona puede considerarse una región más allá del espacio-tiempo clásico y podría poseer propiedades similares a la región Euclídea del instantón asociado a la función de onda de no contorno donde se producen "saltos" cuánticos por efecto túnel entre trayectorias clásicas. De esta forma, en la zona sombreada podría producirse un "salto" entre las trayectorias psi_o´ y psi_o´´.

La pregunta clave que nos hacemos ahora es: ¿En que circunstancias puede producirse esta "rotura" del espacio-tiempo en Universos clásicos como el nuestro? La respuesta es: cuando el Universo es muy pequeño, cuando los campos dominantes son muy ligeros mx<<mplanck, dentro de los agujeros negros y en Universos en expansión donde la constante cosmológica es muy grande. Existe otro caso especial que puede suceder en el horizonte o en el interior de los agujeros negros: el caso donde el valor de la función de onda del Universo se anula por completo.  

El final del espacio-tiempo en un agujero negro  

A continuación vamos a cuantizar un agujero negro de Schwarzschild siguiendo la formulación de la cuantización canónica para obtener la ecuación de Wheeler-DeWitt. La acción de Einstein-Hilbert es:

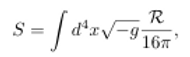
La métrica más genérica para un agujero negro de Schwarzschild puede escribirse:  

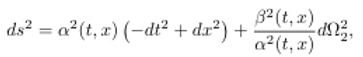
Donde alpha y beta son funciones de t y x. Esto produce la siguiente acción (separando los valores de t y de x):  

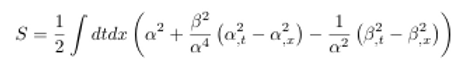
Entonces el Lagrangiano será:

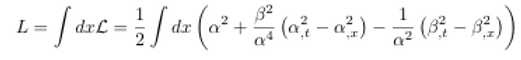
Donde el momento conjugado es:

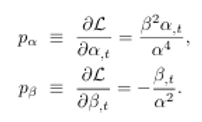
Por tanto los valores de alpha y beta son:

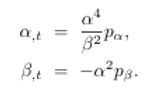
Entonces el Hamiltoniano es:

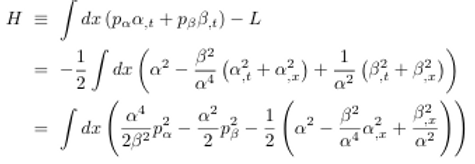
Los conmutadores se definen como:

Donde:

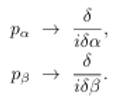
Finalmente obtenemos la buscada ecuación de Wheeler-DeWitt:  

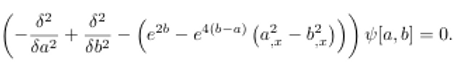
Donde a y b se definen como:

Es ahora cuando llegamos al segundo punto clave: los primeros dos términos de la ecuación de WdW representan la contribución asociada al propio espacio-tiempo mientas que el resto representa una barrera de potencial asociada al campo escalar (materia). Si existiese una región en el Universo en la que ambos términos fuesen iguales la función de onda del Universo sería cero en esa región. Como ya habrán podido adivinar esa región existe y es precisamente una región muy próxima al horizonte de sucesos de un agujero negro.

Esto puede comprobarse fácilmente de la siguiente forma: La función de onda asociada al movimiento del espacio-tiempo es:  

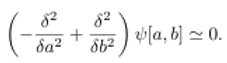
 La solución a esta ecuación son superposiciones de ondas que cumplen:

y

 Ahora analizaremos la función de onda del potencial. Tomaremos el caso del potencial de campana: 

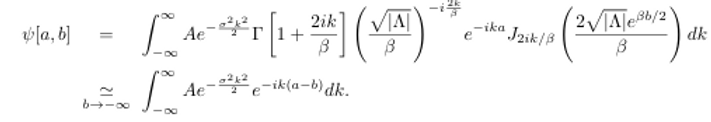
 Esta función es igual a la función de onda asociada al movimiento del espacio-tiempo, por tanto cuando esta onda alcanza la barrera de potencial es absorbida completamente y por tanto la función de onda del Universo en esa zona es cero.  

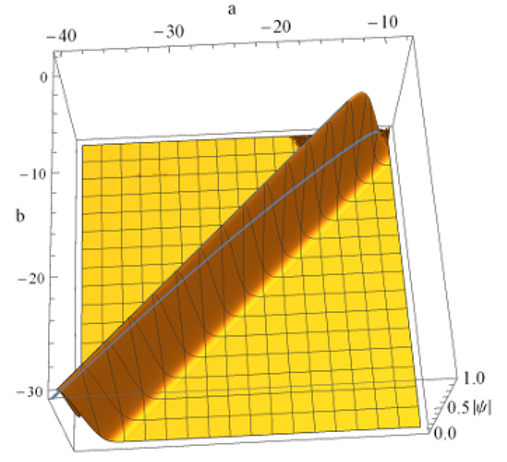
Durante su trayecto hacia el horizonte de sucesos el valor dominante de la función de onda del Universo es el valor clásico (linea de color claro), pero justo cuando alcanza la barrera de potencial en el punto (0,0) la función es completamente absorbida y su valor es cero.

 Pero, entonces ¿significa esto que el espacio-tiempo clásico deja de existir en el horizonte de sucesos? ¿Podemos afirmar que no existe el interior del agujero negro? La interpretación física de la anulación de la función de onda del Universo aún no está clara. Una de las interpretaciones más probables es que esta región representa realmente una superposición de geometrías clásicas.

Una forma de tratar de entender que sucede en esta región es aplicar el llamado principio de incertidumbre generalizado. En varias formulaciones de gravedad cuántica el principio de incertidumbre de Heisenberg es modificado teniendo en cuenta la escala de energía implicada, esta generalización se expresa de la forma:

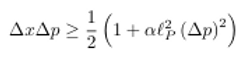
Entonces tenemos que si incrementamos la energía alpha_lp hasta una escala del orden de la energía del agujero negro M tenemos que:

Esto es, la incertidumbre es ¡del orden del diámetro del agujero negro! Esto quiere decir que toda la región del interior del agujero negro entra dentro de la zona puramente cuántica e indeterminada del principio de incertidumbre. ¡El interior del agujero negro no es clásico es una región puramente cuántica y probabilística!  

Las implicaciones para la paradoja de la información en agujeros negros  

Por último veremos como esta nueva visión del Universo como superposición de geometrías puede resolver fácilmente el famoso problema de la información de los agujeros negros. En el proceso colapso de la estrella + formación del agujero negro + evaporación agujero negro hay que considerar todos los trayectos (geometrías) posibles no solamente las trayectorias clásicas. Además de las geometrías que producen un horizonte de eventos existen otras que evitan el horizonte mediante un "salto cuántico" (efecto túnel) comunicando así dos trayectorias clásicas externas al agujero negro. Para estas trayectorias no hay agujero negro y el espacio-tiempo es prácticamente plano. El punto clave es el siguiente: en las primeras etapas del agujero negro las geometrías con horizonte son dominantes pero en las últimas etapas las geometrías sin horizonte son las dominantes. De esta forma la información escapa del agujero negro a partir del tiempo de Page.

Esto puede verse más claramente en la siguiente figura:  

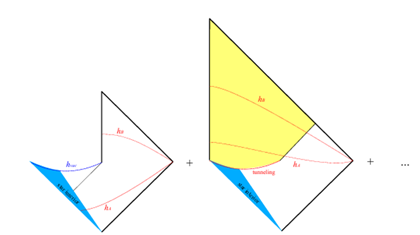
 La línea vertical representa el tiempo, el arco punteado es la singularidad y la línea de 45º delimita el horizonte del agujero negro. Como hemos explicado es necesario sumar sobre todas las geometrías posibles. En la figura izquierda se muestra que la trayectoria dominante al principio hA contiene al agujero negro y por tanto dominan las geometrías con horizonte, sin embargo, según el tiempo avanza la trayectoria dominante hb ya no contiene el horizonte. En la figura de la derecha se muestra que en las últimas etapas del agujero negro ambas trayectorias hA y hB están libres de horizonte y por tanto la información del interior puede escapar libremente.  

Más allá del espacio y el tiempo  

Pero entonces, ¿Cuál es el significado físico de esta región no clásica? ¿Qué sucede realmente dentro de esta región? ¿Puede haber observadores en ella? Dentro de esta región no existe el espacio ni el tiempo por lo que no puede existir ningún tipo de observador. En esta zona la fase de la función de onda del Universo no oscila violentamente lo que produce que no existan las cancelaciones que dan lugar al espacio-tiempo clásico. Esto quiere decir que todas las geometrías permitidas son igual de probables y no se selecciona ninguna trayectoria posible, es decir, esta región es una superposición de posibles trayectos. Esta visión concuerda bien con la región Euclídea (zona con tiempo imaginario) asociada al famoso instantón que origina nuestro Universo clásico en la función de onda de no contorno.

Como si fuéramos exploradores del Universo con poderes "sobrenaturales" la Física fundamental y las Matemáticas nos han permitido viajar hasta una de las regiones más ocultas y fascinantes del Universo: una zona con la capacidad para originar "Universos clásicos" (ramas diferentes de la función de onda) una región más allá del espacio y el tiempo. ¿Alguien podría siquiera imaginar un viaje más increíble?

                                                                                                               

                                                                                                                                 © 2026 JAVIER DE LUCAS