UNA COSA ABSOLUTA

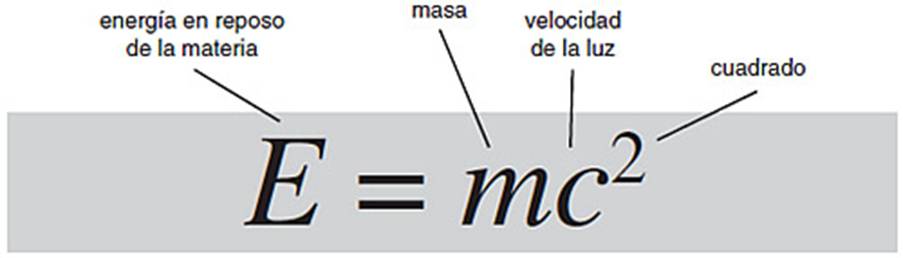
La Relatividad: La materia contiene energía igual a su masa multiplicada por el cuadrado de la velocidad de la luz. La velocidad de la luz es enorme y su cuadrado es absolutamente monumental. Un kilogramo de materia liberaría alrededor del 40 % de la energía en el arma nuclear más grande que jamás ha explotado. Es parte de un paquete de ecuaciones que cambiaron nuestra visión del espacio, tiempo, materia y gravedad. Provocó, indudablemente, física radicalmente nueva. Armas nucleares...solo quizá, aunque no tan directamente o de manera concluyente como los mitos urbanos reclaman. Agujeros negros, el Big Bang, GPS, navegación vía satélite...

Al igual que Albert Einstein, con su mata de pelo alborotada, es el científico arquetípico en la cultura popular, su ecuación E = mc² es la ecuación arquetípica. Es una creencia generalizada que la ecuación llevó a la invención de las armas nucleares, que viene de la teoría de la relatividad de Einstein y que esa teoría (obviamente) tiene algo que ver con varias cosas que son relativas. De hecho, muchos relativistas sociales felizmente corean «todo es relativo», y piensan que tiene algo que ver con Einstein.

No tiene nada que ver. Einstein hizo su teoría «de la relatividad» porque era una modificación de las reglas para el movimiento relativo que se habían usado tradicionalmente en la mecánica newtoniana, donde el movimiento es relativo, dependiendo de un modo simple e intuitivo del sistema de referencia en el que se observa. Einstein tuvo que retocar ligeramente la relatividad newtoniana para que tuviese sentido un descubrimiento experimental desconcertante: que un fenómeno físico particular no es relativo para nada, sino absoluto. A partir de aquí obtuvo un nuevo tipo de física en la cual los objetos se encogen cuando se mueven muy rápido, el tiempo avanza a paso de tortuga y la masa aumenta sin límite. Una extensión que incorpora la gravedad nos ha dado una comprensión mejor de la que ya teníamos de los orígenes del universo y la estructura del cosmos. Está basada en la idea de que el espacio y el tiempo pueden curvarse.

La relatividad es real. El Sistema de Posicionamiento Global (GPS, usado entre otras cosas para la navegación vía satélite de los coches) funciona porque se hicieron las correcciones para los resultados relativistas. Lo mismo es aplicable a los aceleradores de partículas como el Gran Colisionador de Hadrones, que ha anunciado el descubrimiento del bosón de Higgs en 2012, que se cree que es el origen de la masa. Las comunicaciones modernas se han hecho tan rápidas que los mercados están empezando a correr contra una limitación relativista: la velocidad de la luz. Esto es lo más rápido que cualquier mensaje, como por ejemplo una orden en Internet de comprar o vender acciones, puede viajar. Algunos ven esto como una oportunidad de cerrar un trato nanosegundos antes que la competencia, pero, hasta cierto punto, los resultados relativistas no han tenido un efecto serio en las finanzas internacionales. Sin embargo, la gente ya ha calculado las mejores localizaciones para mercados de valores o franquicias. Es solo una cuestión de tiempo.

De cualquier forma, no solo la relatividad no es relativa, incluso la icónica ecuación no es lo que parece. Al principio, cuando Einstein obtuvo la idea física que representa, no la escribió en el modo habitual. No es una consecuencia matemática de la relatividad, aunque se convierte en una si se aceptan varias suposiciones y definiciones físicas. Es quizá típico de la cultura humana que nuestra ecuación más icónica no es, y no fue, lo que parece ser, y tampoco lo es la teoría que la vio nacer. Incluso la conexión con armamento nuclear no es clara, y su influencia histórica en la primera bomba atómica fue pequeña comparada con el peso político de Einstein como el científico icónico.

La «relatividad» cubre dos teorías distintas pero relacionadas: relatividad especial y relatividad general. Usaré la famosa ecuación de Einstein como una excusa para hablar de ambas. La relatividad especial es sobre el espacio, el tiempo y la materia en ausencia de gravedad; la relatividad general también tiene la gravedad en cuenta. Las dos teorías son parte de una gran imagen, pero Einstein tardó diez años de esfuerzo intenso en descubrir cómo modificar la relatividad especial para incorporar la gravedad. Ambas teorías estaban inspiradas por las dificultades en reconciliar la física newtoniana con las observaciones, pero la fórmula icónica surgió en la relatividad especial.

La física parecía bastante sencilla e intuitiva en la época de Newton. El espacio era espacio, el tiempo era tiempo y los dos nunca se deberían encontrar. La geometría del espacio era la de Euclides. El tiempo era independiente del espacio, el mismo para todos los que observaban, siempre que tuviesen sus relojes sincronizados. La masa y el tamaño de un cuerpo no cambiaban cuando se movían y el tiempo siempre pasaba al mismo ritmo por todas partes. Pero cuando Einstein había acabado de reformular la física, todas estas afirmaciones, tan intuitivas que es muy difícil imaginar cómo cualquiera de ellas podría fracasar representando la realidad, resultaron ser erróneas.

No eran totalmente erróneas, por supuesto. Si no hubiesen tenido sentido, entonces el trabajo de Newton nunca habría despegado. La imagen newtoniana del universo físico es una aproximación, no una descripción exacta. La aproximación es extremamente precisa siempre que todo lo involucrado se esté moviendo lo suficientemente lento, y en la mayoría de las circunstancias del día a día ese es el caso. Incluso un avión caza, viajando al doble de la velocidad del sonido, se está moviendo lentamente para este fin. Pero una de las cosas que sí juega un papel en la vida diaria se mueve realmente muy rápido, y establece el criterio para todas las otras velocidades: la luz. Newton y sus sucesores habían demostrado que la luz era una onda y las ecuaciones de Maxwell lo confirmaron. Pero la naturaleza de onda de la luz destapó un nuevo tema. Las olas del mar son ondas en el agua, las ondas del sonido son ondas en el aire, los terremotos son ondas en la Tierra. Así que las ondas de luz eran ondas en... ¿qué?

Matemáticamente, son ondas en el campo electromagnético, que se asume llena todo el espacio. Cuando el campo electromagnético está excitado, persuadido para sustentar electricidad y magnetismo, observamos una onda. Pero ¿qué sucede cuando no está excitado? Sin ondas, un océano, todavía sería un océano, el aire todavía sería aire y la Tierra todavía sería la Tierra. Análogamente, el campo electromagnético todavía sería... el campo electromagnético. Pero no se puede observar el campo electromagnético si no hay electricidad o magnetismo ocurriendo. Si no puedes observarlo, ¿qué es? ¿Existe en realidad? Todas las ondas conocidas en física, excepto las del campo electromagnético, son ondas sobre algo tangible. Los tres tipos de onda —las olas, las del aire y los terremotos— son ondas de movimiento. El medio se mueve de arriba abajo o de un lado a otro, pero normalmente no se desplaza con la onda. (Ata una cuerda larga a una pared y agita un extremo, una onda se desplaza por la cuerda, pero la cuerda no se desplaza por la cuerda.) Hay excepciones: cuando el aire viaja conjuntamente con la onda, lo llamamos «viento», y las olas del mar mueven el agua en la playa cuando se topan con una. Pero incluso aunque describamos un tsunami como una pared de agua en movimiento, no rueda por encima del océano como un balón rueda por un campo.

Generalmente, el agua en una localización determinada se mueve arriba y abajo. Es la localización del «arriba» lo que se mueve. Hasta que el agua se acerca a la orilla, entonces lo que tienes es algo mucho más parecido a una pared en movimiento. La luz, y las ondas electromagnéticas en general, no parecían ser ondas en algo tangible. En la época de Maxwell, y durante cincuenta años o más después, eso era inquietante. La ley de la gravedad de Newton había sido muy criticada porque implicaba que la gravedad, de algún modo, «actúa en la distancia», tan milagroso en un principio filosófico como dar una patada a un balón y marcar gol cuando estás sentado en las gradas. Decir que es transmitido por «el campo gravitacional» no explica realmente qué está sucediendo. Lo mismo sucede con el electromagnetismo. Así que los físicos se convencieron con la idea de que había algún medio, nadie sabía qué, lo llamaron el «éter luminoso» o simplemente «éter», que sustentaba a las ondas electromagnéticas. Las vibraciones se desplazan más rápido cuanto más rígido es el medio y la luz era muy rápida, de modo que el éter tenía que ser sumamente rígido. Aunque los planetas se podían mover a través de él sin resistencia. Al no haberse detectado con facilidad, el éter no debía tener masa, ni viscosidad, ser incomprimible y ser totalmente transparente a todas las formas de radiación.

Era una combinación de atributos sobrecogedora, pero casi todos los físicos asumieron que el éter existía, porque la luz claramente hacía lo que hacía. Algo tenía que llevar la onda. Además, la existencia del éter podía en principio detectarse, porque otra característica de la luz sugería un modo de observarlo. En un vacío, la luz se mueve con una velocidad fija c. La mecánica newtoniana había enseñado a todo físico a preguntar: ¿velocidad relativa a qué? Si mides la velocidad en dos sistemas de referencia diferentes, uno moviéndose con respecto a otro, obtienes respuestas diferentes. La constancia de la velocidad de la luz sugería una respuesta obvia: relativa al éter. Pero esto era un poco simplista, porque dos sistemas de referencia que se están moviendo uno con respecto al otro no pueden ser ambos relativos al éter en reposo.

A medida que la Tierra se abre paso a través del éter, que milagrosamente no se resiste, va dando vueltas alrededor del Sol. En puntos opuestos de su órbita, se está moviendo en direcciones opuestas. De modo que por la mecánica newtoniana, la velocidad de la luz debería variar entre los dos extremos: c más una contribución del movimiento de la Tierra relativo al éter, y c menos la misma contribución. Mide la velocidad, mídela seis meses más tarde, encuentra la diferencia, si hay una, y has probado que el éter existe. A finales del siglo XIX, se llevaron a cabo muchos experimentos siguiendo esta línea, pero los resultados no eran concluyentes. Por lo tanto no había diferencia, o había una pero el método experimental no era suficientemente preciso. Peor, la Tierra quizá estuviese arrastrando el éter con ella. Esto explicaría simultáneamente por qué la Tierra podía moverse a través de un medio tan rígido sin resistencia e implicaría que no deberíamos ver ninguna diferencia en la velocidad de la luz. El movimiento de la Tierra relativo al éter sería siempre cero.

En 1887, Albert Michelson y Edward Morley llevaron a cabo uno de los experimentos físicos más famosos de todos los tiempos. Sus aparatos fueron diseñados para detectar variaciones extremadamente pequeñas en la velocidad de la luz en dos direcciones, perpendicular la una a la otra. Como la Tierra se estaba moviendo en relación con el éter, no podría moverse con las mismas velocidades relativas en dos direcciones diferentes... a menos que se diese la coincidencia de que se estuviese moviendo a lo largo de la línea que dividía en dos estas direcciones, en cuyo caso bastaría que rotases el aparato un poco y lo intentases de nuevo.

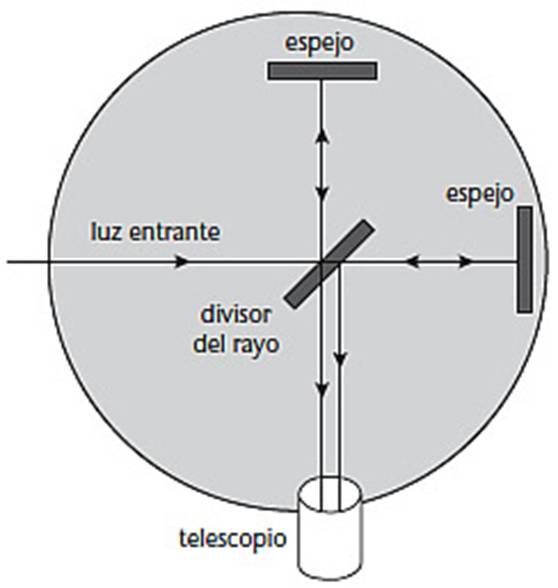
Experimento de Michelson-Morley.

El aparato (figura), era lo suficientemente pequeño para que pudiese estar en una mesa de laboratorio. Usaba un espejo semiplateado para dividir un rayo de luz en dos partes, una pasando a través del espejo y la otra reflejándose en un ángulo recto. Cada rayo por separado se reflejaba de vuelta a lo largo de su trayectoria y los dos rayos combinados de nuevo chocaban con un detector. El aparato se ajustaba para hacer las trayectorias de la misma longitud. El rayo original se establecía para ser coherente, lo que quiere decir que sus ondas estaban en sincronía unas con otras, todas tenían la misma fase, picos coincidiendo con picos. Cualquier diferencia entre la velocidad de la luz en las direcciones seguidas por los dos rayos causaría que sus fases cambiasen la una con respecto a la otra, de modo que sus picos estarían en lugares diferentes. Esto causaría interferencia entre las dos ondas, resultando un patrón a rayas de «franjas de difracción». El movimiento de la Tierra relativo al éter causaría que las franjas se moviesen. El efecto sería diminuto; una vez determinado lo que se conocía del movimiento de la Tierra respecto al Sol, las franjas de difracción se moverían alrededor de un 4 % de ancho de una franja. Usando múltiples reflexiones, esto podría aumentar al 40 %, que es lo suficientemente grande para detectarse. Para evitar la posible coincidencia de la Tierra moviéndose exactamente a lo largo del bisector de los dos rayos, Michelson y Morley hacían flotar el aparato en un baño de mercurio, de manera que podía girarse fácil y rápidamente. Debería entonces ser posible observar las franjas moviéndose con igual rapidez.

Fue un experimento cuidadoso y preciso. Su resultado fue totalmente negativo. Las franjas no se movieron el 40 % de su ancho. Hasta donde alguien podría decir con certeza, no se movieron para nada. Experimentos posteriores, capaces de detectar una alteración de un 0,07 % del ancho de la franja, también dieron un resultado negativo. El éter no existía. Este resultado no solo descartaba al éter, también amenazaba con descartar la teoría de Maxwell del electromagnetismo. Implicaba que la luz no se comportaba de una manera newtoniana, relativa a sistemas de referencia móviles. Este problema puede remontarse directamente a las propiedades matemáticas de las ecuaciones de Maxwell y cómo se transforman en relación con un sistema móvil.

El físico y químico irlandés George FitzGerald y el físico holandés Hendrik Lorenz sugirieron de manera independiente (en 1892 y 1895, respectivamente) un modo audaz de sortear el problema. Si un cuerpo moviéndose se contrae ligeramente en su dirección de movimiento, justo la cantidad correcta, entonces el cambio en la fase que el experimento de Michelson-Morley estaba esperando detectar se contrarrestaría de manera exacta con el cambio en la longitud de la trayectoria que la luz estaba siguiendo. Lorenz mostró que esta «contracción de Lorenz-FitzGerald» solucionaba, también, las dificultades matemáticas de las ecuaciones de Maxwell. El descubrimiento conjunto mostró que los resultados de los experimentos en electromagnetismo, incluyendo la luz, no dependían del movimiento relativo del sistema de referencia. Poincaré, que también había estado trabajando en una línea similar, añadió su convincente peso intelectual a la idea.

El escenario estaba ahora preparado para Einstein. En 1905, desarrolló y amplió las especulaciones previas sobre una nueva teoría de movimiento relativo en un artículo «On the electrodynamics of moving bodies» (Sobre la electrodinámica de los cuerpos en movimiento). Su trabajo fue más allá que el de sus predecesores en dos sentidos. Mostró que el cambio necesario para la formulación matemática del movimiento relativo era más que un truco para arreglar el electromagnetismo. Se necesitaba para todas las leyes físicas. Entendió que las nuevas matemáticas debían ser una descripción genuina de la realidad, con el mismo estatus filosófico que había sido acordado para la descripción newtoniana reinante, pero proporcionando una concordancia mejor con los experimentos. Era física real.

La visión del movimiento relativo empleada por Newton se remontaba incluso más allá, a Galileo. En su Dialogo “sopra i due massimi sistemi del mondo” (Diálogo sobre los dos máximos sistemas del mundo) Galileo hablaba de un barco viajando a velocidad constante en un mar totalmente en calma, y argumentaba que ningún experimento en mecánica llevado a cabo bajo cubierta podría revelar que el barco se estaba moviendo. Esto es el principio de la relatividad de Galileo: en mecánica, no hay diferencia entre las observaciones hechas en dos sistemas que se están moviendo con una velocidad uniforme uno con respecto al otro. En concreto, no hay un sistema especial de referencia que esté «en reposo». El punto de arranque de Einstein fue el mismo principio, pero con una vuelta de tuerca extra: debe aplicarse no solo a la mecánica, sino a todas las leyes de la física. Entre ellas, por supuesto, están las ecuaciones de Maxwell y la constancia de la velocidad de la luz.

Para Einstein, el experimento de Michelson-Morley era una pequeña pieza de evidencia extra, pero no era la prueba. La prueba de que su nueva teoría era correcta recaía en su principio extendido de la relatividad y lo que implicaba para la estructura matemática de las leyes de la física. Si puedes aceptar el principio, todo lo demás lo sigue. Este es el motivo de que la teoría fuese conocida como «relatividad». No porque «todo es relativo», sino porque tienes en cuenta la manera en la que todo es relativo. Y no es lo que esperabas. Esta versión de la teoría de Einstein es conocida como relatividad especial porque se aplica solo en sistemas de referencia que se están moviendo uniformemente el uno con respecto al otro. Entre sus consecuencias están las contracciones de Lorenz-FitzGerald, ahora interpretadas como una característica necesaria del espacio-tiempo. De hecho, había tres efectos relacionados. Si un sistema de referencia se está moviendo de manera uniforme respecto a otro, entonces las longitudes medidas en el sistema se contraen a lo largo de la dirección del movimiento, la masa aumenta y el tiempo avanza más lentamente. Estos tres efectos están atados unos a otros por las leyes básicas de conservación de la energía y el momento, una vez aceptas uno de ellos, los otros son consecuencias lógicas.

La formulación técnica de estos efectos es una fórmula que describe cómo se relacionan mediciones en un sistema con las correspondientes en el otro. El resumen es: si un cuerpo pudiese moverse próximo a la velocidad de la luz, entonces su longitud se haría muy pequeña, el tiempo avanzaría muy lentamente y su masa se haría muy grande. Tan solo daré una idea de las matemáticas: la descripción física no debería tomarse demasiado literalmente y llevaría demasiado establecerla en el lenguaje correcto. Todo viene de... el teorema de Pitágoras. Una de las ecuaciones más antiguas en ciencias lleva a una de las más nuevas.

Supongamos que una nave espacial está pasando por encima de nuestras cabezas con velocidad v y la tripulación realiza un experimento. Envía una secuencia de luz desde el suelo de la cabina al techo y la medición del tiempo es T. Mientras un observador en el suelo observa el experimento a través de un telescopio (asumiendo que la nave espacial es transparente) y mide el tiempo como t.

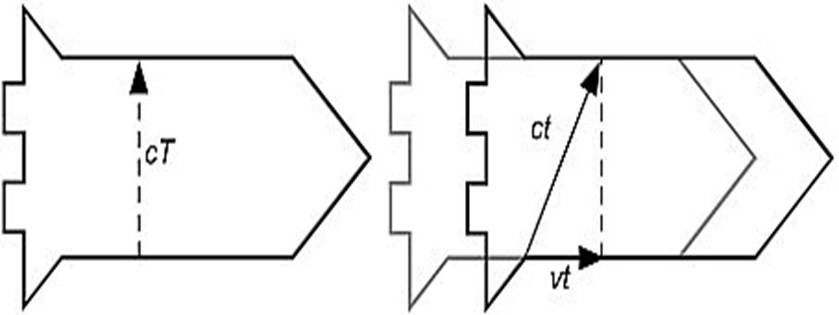
A la izquierda: el experimento en el sistema de referencia de la tripulación. A la derecha: el mismo experimento en el sistema de referencia del observador desde el suelo. El gris muestra la posición de la nave vista desde el suelo cuando el rayo de luz empieza su viaje; el negro muestra la posición de la nave cuando la luz completa su viaje.

La figura (izquierda) muestra la geometría del experimento desde el punto de vista de la tripulación. Para ellos, la luz ha ido derecha hacia arriba. Como la luz viaja a una velocidad c, la distancia que se desplaza es cT, mostrada con la flecha punteada. La figura (derecha) muestra la geometría del experimento desde el punto de vista del observador desde el suelo. La nave espacial se ha movido una distancia vt, de modo que la luz se ha desplazado diagonalmente. Como la luz también se desplaza a una velocidad c para el observador desde el suelo, la diagonal tiene una longitud ct. Pero la línea de puntos tiene la misma longitud que la línea de puntos en la primera imagen, en concreto, cT. Por el teorema de Pitágoras:

(ct)² = (CT)2 + (vt)²

Despejamos T, y obtenemos:

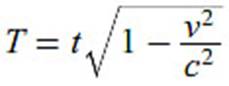
 Que es más pequeño que t. Para obtener la contracción de Lorenz-FitzGerald, ahora nos imaginamos que la nave espacial viaja a un planeta a una distancia de la Tierra x a velocidad v. Entonces el tiempo transcurrido es t = x/v. Pero la fórmula previa muestra que para la tripulación, el tiempo que tarda es T, no t. Para ellos, la distancia X debe satisfacer T = X/v. Por lo tanto:

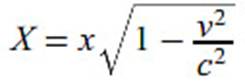
Que es más pequeña que x. La obtención del cambio de masa es ligeramente más complicada y depende de una interpretación concreta de la masa, «masa en reposo», de modo que no daré detalles. La fórmula es:

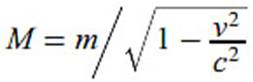
Que es mayor que m. Estas ecuaciones nos dicen que hay algo muy especial en la velocidad de la luz (y por tanto en la luz). Una consecuencia importante de este formalismo es que la velocidad de la luz es una barrera impenetrable. Si un cuerpo arranca más lento que la luz, no puede acelerarse a una velocidad mayor que la de la luz. En septiembre de 2011, físicos que trabajaban en Italia anunciaron que las partículas subatómicas llamadas neutrinos parecían estar viajando más rápido que la luz. Su observación es polémica, pero si se confirma, (aún no lo ha hecho, 2025, ni creo que lo hará), llevaría a una nueva física importante.

Pitágoras aparece en la relatividad de otras maneras. Una es la formulación de la relatividad especial en términos de la geometría del espacio-tiempo, originalmente introducida por Hermann Minkowski. El espacio ordinario newtoniano puede capturarse matemáticamente haciendo corresponder sus puntos con tres coordenadas (x, y, z), y definiendo la distancia d entre dicho punto y otro (X, Y, Z) con el teorema de Pitágoras:

d² = (x – X)² + (y – Y)² + (z – Z)²

Ahora hacemos la raíz cuadrada para obtener d. El espacio-tiempo de Minkowski es similar, pero ahora hay cuatro coordenadas (x, y, z, t), tres del espacio más una del tiempo, y un punto se llama suceso, una localización en el espacio, observado en un tiempo específico. La fórmula de la distancia es muy similar:

d² = (x – X)² + (y – Y)² + (z – Z)² – c²(t – T)²

El factor c² es solo una consecuencia de las unidades usadas para medir el tiempo, pero el signo menos delante es crucial. La «distancia» d es llamada el intervalo y la raíz cuadrada es real solo cuando la parte derecha de la ecuación es positiva. Lo que se reduce a la distancia espacial entre los dos sucesos siendo mayor que la diferencia temporal (en unidades correctas: años luz y años, por ejemplo). Eso, a su vez, significa que en principio un cuerpo podría desplazarse desde el primer punto en el espacio en el primer tiempo y llegar al segundo punto en el espacio en el segundo tiempo, sin ir más rápido que la luz.

En otras palabras, el intervalo es real si, y solo si, es físicamente posible, en principio, desplazarse entre dos sucesos. El intervalo es cero si, y solo si, la luz puede desplazarse entre ellos. Esta región físicamente accesible se llama el cono de luz de un suceso y viene en dos partes: el pasado y el futuro. La siguiente figura muestra la geometría cuando el espacio está reducido a una dimensión.

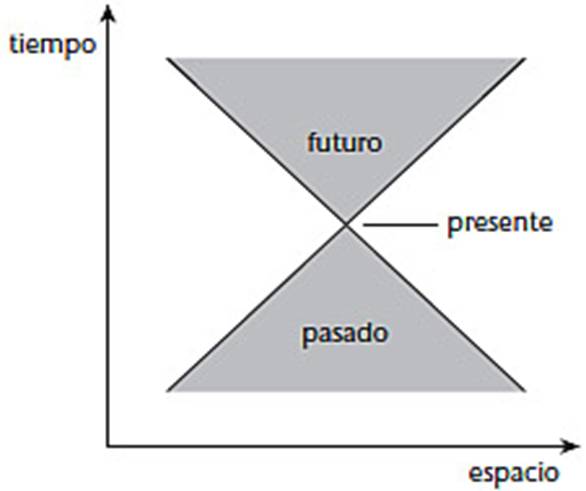
Espacio-tiempo de Minkowski, con el espacio mostrado como unidimensional.

Ahora he mostrado tres ecuaciones relativistas y bosquejado cómo surgen, pero ninguna de ellas es la icónica ecuación de Einstein. Sin embargo, ahora estamos listos para entender cómo la obtuvo, una vez apreciemos una innovación más de la física de principios del siglo XX.

Como hemos visto, los físicos habían realizado con anterioridad experimentos para demostrar de manera concluyente que la luz era una onda, y Maxwell había demostrado que era una onda electromagnética. Sin embargo, en 1905, estuvo claro que a pesar del peso de la evidencia para la naturaleza en forma de onda de la luz, hay circunstancias en las cuales se comporta como una partícula. Ese año Einstein usó esta idea para explicar algunas características del efecto fotoeléctrico, en el que la luz que choca con un metal apropiado genera electricidad. Argumentó que los experimentos tenían sentido solo si la luz llegaba en paquetes discretos, a todos los efectos, partículas. Ahora se llaman fotones. Este desconcertante descubrimiento era uno de los pasos clave hacia la mecánica cuántica. Curiosamente, esta idea de la mecánica cuántica intrínsecamente era vital para la formulación de la relatividad de Einstein. Para obtener su ecuación relacionando masa con energía, Einstein pensó en qué le sucede a un cuerpo que emite un par de fotones. Para simplificar los cálculos, restringió la atención a una dimensión del espacio, de modo que el cuerpo se movía a lo largo de una línea recta. Esta simplificación no afecta a la respuesta.

La idea básica es considerar el sistema en dos sistemas de referencia diferentes. Uno se mueve con el cuerpo, de modo que el cuerpo parece estar parado en ese sistema. El otro sistema se mueve con una velocidad relativa al cuerpo pequeña pero distinta de cero. Permíteme llamarlos el sistema estacionario y el sistema en movimiento. Son como la nave espacial (en su propio sistema de referencia está detenida) y mi observador terrestre (para quien la nave parece estar en movimiento). Einstein asumió que los dos fotones son igualmente energéticos, pero emitidos en direcciones opuestas. Sus velocidades son iguales y opuestas, de modo que la velocidad del cuerpo (en cualquier marco) no cambia cuando los fotones se emiten. Entonces calculaba la energía del sistema antes de que el cuerpo emitiese el par de fotones, y después. Al asumir que la energía debe conservarse, obtuvo una expresión que relaciona el cambio en la energía del cuerpo, provocada por la emisión de fotones, con el cambio en su masa (relativista). El resultado fue:

(cambio en la energía) = (cambio en la masa) × c²

Haciendo la suposición razonable de que un cuerpo de masa cero tiene energía cero, entonces tenemos que:

energía = masa × c²

Esto, por supuesto, es la fórmula famosa, en la que E simboliza la energía y m la masa. Además de hacer los cálculos, Einstein tuvo que interpretar su significado. En concreto, expuso que en un sistema para el cual el cuerpo está en reposo, la energía dada por la fórmula debería considerarse como su energía «interna», que posee porque está hecho de partículas subatómicas, y cada una tiene su propia energía. En un sistema en movimiento, hay también una contribución de la energía cinética. Hay otras sutilezas matemáticas también, tales como el uso de una velocidad pequeña y aproximaciones a las fórmulas exactas.

A Einstein con frecuencia se le atribuye el mérito, si esa es la palabra, de la comprensión de que una bomba atómica liberaría cantidades de energía tremendas. Ciertamente esa impresión dio la revista Time en julio de 1946 cuando puso su cara en la cubierta con una nube de hongo atómica tras él con su ecuación icónica. La conexión entre la ecuación y una explosión enorme parece clara; la ecuación nos dice que la energía inherente en cualquier objeto es su masa multiplicada por el cuadrado de la velocidad de la luz. Como la velocidad de la luz es enorme, su cuadrado es todavía mayor, lo cual identifica mucha energía en una pequeña cantidad de materia. La energía en un gramo de materia resulta ser 90 terajulios, equivalente más o menos a la producción de un día de electricidad de una central de energía nuclear.

Sin embargo, no ocurre así. La energía liberada en una bomba atómica es solo una pequeña fracción de la masa en reposo relativista y los físicos ya son conscientes, por motivos experimentales, que ciertas reacciones nucleares podrían liberar mucha energía. El principal problema técnico era mantener junto un pedazo de material radiactivo adecuado durante el tiempo suficiente para que se provocase una reacción en cadena, que creciese exponencialmente, en la cual la descomposición de un átomo radiactivo sea la causante de emitir radiaciones que desencadenen el mismo efecto en otros átomos. Sin embargo, la ecuación de Einstein rápidamente comenzó a establecerse en la mente del público como la progenitora de la bomba atómica. El Informe Smyth, un documento del gobierno de Estados Unidos dado a conocer al público para explicar la bomba atómica, coloca la ecuación en su segunda página. Sospecho que lo que pasó es lo que Jack Cohen llamó «mentiras a los niños», historias simplificadas dichas con propósitos legítimos, que pavimentan el camino a una explicación más precisa. Esto mueo funciona la educación: la historia completa es siempre demasiado complicada para cualquiera excepto para los expertos y ellos saben tanto que no creen la mayoría de ello.

Sin embargo, la ecuación de Einstein no puede ser descartada sin más. Sí desempeñó un papel en el desarrollo de armas nucleares. La noción de fisión nuclear, que impulsa la bomba atómica, surge de discusiones entre los físicos Lise Meitner y Otto Frisch en la Alemania nazi en 1938. Estaban intentando comprender las fuerzas que mantienen al átomo junto, las cuales son un poco como la tensión de la superficie de una gota de un líquido. Estaban fuera paseando, discutiendo sobre física y aplicaron la ecuación de Einstein para averiguar si la fisión era posible por motivos energéticos. Frisch posteriormente escribió:

“Ambos nos sentamos en el tronco de un árbol y empezamos a calcular en pedacitos de papel ... Cuando las dos gotas se separan, se alejarían por repulsión eléctrica, sobre 200 MeV en total. Afortunadamente Lise Meitner recordó cómo calcular las masas de los núcleos ... y calculó que los dos núcleos formados ... serían más ligeros alrededor de un quinto de la masa de un protón ... según la fórmula de Einstein E = mc2 ... la masa era justo equivalente a 200 MeV. ¡Todo encajaba!”

Aunque E = mc² no era directamente responsable de la bomba atómica, fue uno de los grandes descubrimientos en física que llevó a una comprensión teórica efectiva de las reacciones nucleares. El papel más importante de Einstein en lo que a la bomba atómica se refiere fue político. Alentado por Leo Szilard, Einstein escribió al presidente Roosevelt advirtiendo que los nazis podrían estar desarrollando armas atómicas y explicándole su asombrosa potencia. Su reputación e influencia eran enormes y el presidente hizo caso de la advertencia. El Proyecto Manhattan, Hiroshima y Nagasaki, y la consiguiente Guerra Fría fueron solo algunas de las consecuencias.

Einstein no estaba satisfecho con la relatividad especial. Proporcionaba una teoría unificada del espacio, tiempo, materia y electromagnetismo, pero excluía un ingrediente fundamental. La gravedad. Einstein creía que «todas las leyes de la física» deben satisfacer su versión extendida del principio de relatividad de Galileo. La ley de la gravedad seguramente debería estar entre ellas. Pero eso no ocurría en la versión actual de la relatividad. La ley de la inversa del cuadrado de Newton no se transformaba correctamente entre sistemas de referencia. Así que Einstein decidió que tenía que cambiar la ley de Newton. Ya había cambiado prácticamente todo lo demás en el universo newtoniano, así que ¿por qué no?

Le llevó diez años. Su punto de partida fue averiguar las implicaciones del principio de relatividad para un observador moviéndose libremente bajo la influencia de la gravedad, por ejemplo, en un ascensor que cae libremente. Finalmente se dirigió a una formulación apropiada. En esto recibió la ayuda de un amigo cercano, el matemático Marcel Grossmann, que lo dirigió hacia un campo de las matemáticas que estaba creciendo rápidamente: la geometría diferencial. Este había sido desarrollado a partir del concepto de variedad de Riemann y su caracterización de curvatura. La métrica de Riemann puede escribirse como una matriz 3 × 3, y que técnicamente este es un tensor simétrico. Una escuela de matemáticos italianos, en particular Tullio Levi-Civita y Gregorio Ricci-Curbastro, retomaron las ideas de Riemann y las transformaron en el cálculo tensorial.

Desde 1912, Einstein estaba convencido de que la clave para una teoría relativista de la gravedad le requería reformular sus ideas usando el cálculo tensorial, pero en un espacio-tiempo tetradimensional más que en un espacio tridimensional. Los matemáticos estaban felizmente siguiendo a Riemann y permitiendo cualquier número de dimensiones, de modo que ya habían establecido las cosas en una generalidad más que suficiente. Para acortar la historia, finalmente obtuvo lo que ahora llamamos las ecuaciones del campo de Einstein, que escribió como:

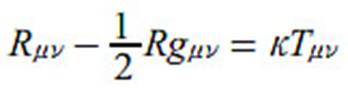
Aquí R, g y T son tensores —cantidades que definen las propiedades físicas y se transforman según las reglas de la geometría diferencial— y κ es una constante. Los subíndices μ y ν repasan las cuatro coordenadas del espacio-tiempo, de manera que cada tensor es una tabla 4 × 4 de 16 números. Ambos son simétricos, lo que quiere decir que no cambian cuando μ y ν se intercambian, lo que reduce la lista a 10 números distintos. Así que la fórmula realmente esconde 10 ecuaciones, motivo por el que con frecuencia nos referimos a ellas usando el plural, comparable a las ecuaciones de Maxwell. R es la métrica de Riemann, define la forma del espacio-tiempo. g es el tensor de curvatura de Ricci, que es una modificación de la noción de curvatura de Riemann. Y T es el tensor de energía-momento, que describe cómo estas dos cantidades fundamentales dependen del suceso espacio-tiempo que nos ocupa. Einstein presentó su ecuación a la Academia de Ciencias prusiana en 1915. Llamó a su nuevo trabajo la teoría de la relatividad general.

Podemos interpretar las ecuaciones de Einstein geométricamente, y cuando lo hacemos, proporcionan una nueva aproximación a la gravedad. La innovación básica es que la gravedad no está representada como una fuerza, sino como la curvatura del espacio-tiempo. En ausencia de gravedad, el espacio-tiempo se reduce al espacio de Minkowski. La fórmula para el intervalo determina el tensor de curvatura correspondiente. Su interpretación es «no curvada», de la misma manera que el teorema de Pitágoras se aplica a un plano llano, pero no a un espacio no euclidiano curvado positiva o negativamente. El espacio-tiempo de Minkowski es plano. Pero cuando aparece la gravedad, el espacio-tiempo se curva.

El modo habitual de imaginarlo es olvidarse del tiempo, bajar las dimensiones del espacio a dos y obtener algo como en la siguiente figura (izquierda). El plano llano del espacio(-tiempo) de Minkowski está distorsionado, mostrado aquí por una curva concreta que crea una depresión. Lejos de la estrella, la materia o la luz se desplazan en una línea recta (punteada). Pero la curvatura provoca que la trayectoria se curve. De hecho, parece superficialmente como si alguna fuerza proveniente de la estrella atrajese la materia hacia ella. Pero no hay fuerza, solo espacio-tiempo combado. Sin embargo, esta imagen de la curvatura deforma el espacio a lo largo de una dimensión extra, que no se necesita matemáticamente. Una imagen alternativa es dibujar una rejilla de geodésicas, las trayectorias más cortas que distan lo mismo unas de otras según la métrica curva. Estas se amontonan donde la curvatura es mayor (figura, derecha).

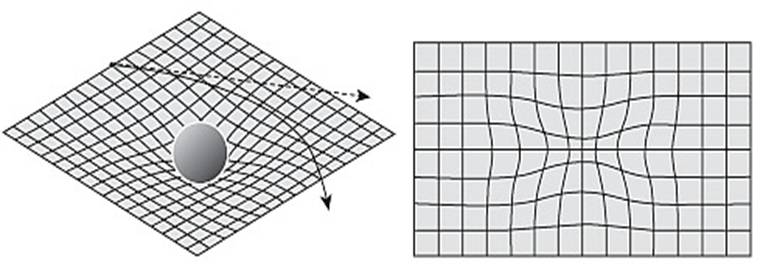
A la izquierda: espacio combado cerca de una estrella, y cómo curva la trayectoria de materia o luz que están pasando. A la derecha: imagen alternativa usando una rejilla de geodésicas, las cuales se amontonan en regiones de curvaturas más altas.

Si la curvatura del espacio-tiempo es pequeña, esto es, si lo que (en la imagen antigua) pensamos como fuerzas gravitacionales no son demasiado grandes, entonces esta formulación nos lleva a la ley de la gravedad de Newton. Comparando las dos teorías, la constante de Einstein κ resulta ser

8πG/c4

donde G es la constante gravitacional de Newton. Esto vincula la nueva teoría con la anterior y prueba que en la mayoría de los casos la nueva estará de acuerdo con la antigua. La nueva física interesante se da cuando esta ya no es cierta, cuando la gravedad es grande. Cuando Einstein propuso esta teoría, cualquier prueba de relatividad tenía que hacerse fuera del laboratorio, a gran escala. Lo que quiere decir astronomía. Einstein, por lo tanto, fue buscando peculiaridades inexplicables en el movimiento de los planetas, efectos que no concordasen con Newton. Encontró una que podría ser adecuada: una característica confusa de la órbita de Mercurio, el planeta más cercano al Sol, sujeto a las mayores fuerzas gravitacionales, y en consecuencia, si Einstein tenía razón, dentro de una región de curvatura mayor.

Como todos los planetas, Mercurio sigue una trayectoria que es muy próxima a una elipse, de modo que algunos puntos en su órbita están más próximos al Sol que otros. Los más próximos de todos se llaman su perihelio («cerca del Sol» en griego). La localización exacta de este perihelio había sido observada durante muchos años, y había algo extraño en ella. El perihelio lentamente rotaba alrededor del Sol, un efecto llamado precesión; en efecto, el eje largo de la elipse orbital estaba lentamente cambiando de dirección. Eso estaba bien, las leyes de Newton lo predecían, porque Mercurio no es el único planeta del Sistema Solar y los otros planetas estaban lentamente cambiando su órbita. El problema era que los cálculos newtonianos daban la velocidad de precesión equivocada. Los ejes estaban rotando demasiado rápido.

Esto se sabía desde 1840, cuando François Arago, director del Observatorio de París, pidió a Urbain Le Verrier que calculase la órbita de Mercurio usando las leyes de movimiento y gravitación de Newton. Pero cuando los resultados se probaron observando el cronometraje exacto de un tránsito de Mercurio —un paso delante del Sol, visto desde la Tierra— vieron que estaban equivocados. Le Verrier decidió intentarlo de nuevo, eliminando las potenciales fuentes de error, y en 1859 publicó sus nuevos resultados. En el modelo newtoniano, la velocidad de precesión tenía un margen de error de un 0,7 %. La diferencia comparada con las observaciones era minúscula: 38 segundos de arco cada siglo (más tarde se modificó a 43 arcosegundos). No es mucho, menos que una diezmilésima de un grado por año, pero era suficiente para interesar a Le Verrier. En 1846 había construido su reputación analizando irregularidades en la órbita de Urano y prediciendo la existencia, y localización, de un planeta, por aquel entonces por descubrir: Neptuno. Ahora estaba esperando repetir la hazaña. Interpretó el movimiento inesperado del perihelio como la prueba de que algún mundo desconocido estaba alterando la órbita de Mercurio. Hizo los cálculos y predijo la existencia de un pequeño planeta con una órbita más próxima al Sol que la de Mercurio. Incluso tenía un nombre para él: Vulcano, el dios romano del fuego.

Observar a Vulcano, si existía, sería difícil. El resplandor del Sol era un obstáculo, de modo que la mejor apuesta era coger a Vulcano en tránsito, donde hubiese un diminuto punto oscuro en el brillante disco solar. Poco después de la predicción de Le Verrier, un astrónomo aficionado llamado Edmond Lescarbault notificó al famoso astrónomo que acababa de ver justo eso. Inicialmente asumió que el punto debía ser una mancha solar, pero se movía a la velocidad equivocada. En 1860, Le Verrier anunció el descubrimiento de Vulcano a la Academia de Ciencias de París, y el gobierno premio a Lescarbault con la prestigiosa Legión de Honor.

En medio del clamor, algunos astrónomos no acababan de estar convencidos. Uno fue Enmmanuel Liais, quien había estado estudiando el Sol con un equipo mucho mejor que el de Lescarbault. Su reputación estaba en peligro: había estado observando el Sol para el gobierno brasileño, habría sido vergonzoso no haber visto algo de tanta importancia. Él negó rotundamente que hubiese algún tránsito. Durante un tiempo, todo fue muy confuso. Los aficionados reclamaban repetidamente que habían visto a Vulcano, a veces, años antes de que Le Verrier anunciase su predicción. En 1878, James Watson, un profesional, y Lewis Swift, un aficionado, dijeron que habían visto un planeta como Vulcano durante un eclipse solar. Le Verrier había muerto un año antes, todavía convencido de que había descubierto un nuevo planeta cerca del Sol, pero sin sus nuevos cálculos de órbitas y predicciones de tránsitos entusiastas, ninguno de los cuales había sucedido, el interés en Vulcano rápidamente se desvaneció. Los astrónomos se hicieron escépticos.

En 1915, Einstein dio el tiro de gracia. Reanalizó el movimiento usando la relatividad general, sin asumir ningún planeta nuevo, y un cálculo sencillo y transparente le llevó a un valor de 43 segundos de arco para la precesión, la cifra exacta obtenida actualizando los cálculos originales de Le Verrier. Un moderno cálculo newtoniano predice una precesión de 5.560 arcosegundos por siglo, pero las observaciones dan 5.600. La diferencia es 40 segundos de arco, de modo que alrededor de 3 arcosegundos por siglo sigue sin aparecer. El anuncio de Einstein hizo dos cosas: fue visto como una confirmación de la relatividad, y en lo que a la mayoría de los astrónomos se refería, relegaba a Vulcano al montón de desechos. Otra verificación astronómica famosa de la relatividad general es la predicción de Einstein de que el Sol curva la luz. La gravitación newtoniana también predice esto, pero la relatividad general predice una cantidad de curvamiento que es dos veces mayor.

El eclipse solar total de 1919 proporcionó una oportunidad para distinguir los dos, y Sir Arthur Eddington organizó una expedición, finalmente anunciando que Einstein se imponía. Esto fue aceptado con entusiasmo en la época, pero más tarde se hizo claro que los datos eran pobres y el resultado fue cuestionado. Observaciones independientes adicionales de 1922 parecían estar de acuerdo con la predicción relativista, como lo estuvo un reanálisis posterior de los datos de Eddington. En la década de los sesenta del siglo XX, se hizo posible hacer las observaciones para radiaciones de radiofrecuencia y, solo entonces, fue seguro que los datos sí que mostraban una desviación dos veces mayor que la predicha por Newton e igual a la que predijo Einstein.

Las predicciones más dramáticas de la relatividad general surgen en una escala mucho más grande: los agujeros negros, que nacen cuando una estrella de gran masa se colapsa bajo su propia gravitación, y el universo en expansión, actualmente explicado por el Big Bang. Las soluciones para las ecuaciones de Einstein son geometrías del espacio-tiempo. Estas representarían el universo como un todo, o alguna parte de él, asumiendo que esté aislado gravitacionalmente de modo que el resto del universo no tiene un efecto importante. Esto es análogo a suposiciones newtonianas anteriores de que solo dos cuerpos están interaccionando, por ejemplo. Como las ecuaciones de campo de Einstein involucran a diez variables, las soluciones explícitas en términos de fórmulas matemáticas son raras. Hoy podemos solucionar las ecuaciones numéricamente, pero eso era una quimera antes de la década de los sesenta del siglo pasado, porque los ordenadores no existían o eran demasiado limitados para resultar útiles. El modo estándar de simplificar ecuaciones es invocar a la simetría.

Supongamos que las condiciones iniciales para el espacio-tiempo son simétricas esféricamente, esto es, todas las cantidades físicas dependen solo de la distancia al centro. Entonces el número de variables en cualquier modelo se reduce considerablemente. En 1916 el astrofísico alemán Karl Schwarzschild hizo esta suposición para las ecuaciones de Einstein y se las arregló para resolver las ecuaciones resultantes con una fórmula exacta, conocida como la métrica Schwarzschild. Su fórmula tiene una característica curiosa: una singularidad. La solución se hace infinita a una distancia concreta del centro, llamada radio de Schwarzschild. Al principio se asumía que esta singularidad era algún tipo de artefacto matemático, y su significado físico era tema de una discusión importante. Ahora la interpretamos como el horizonte de sucesos de un agujero negro.

Imaginemos ahora una estrella con una masa tan grande que su radiación no puede contrarrestar su campo gravitacional. La estrella empezará a contraerse, absorbida por su propia masa. Cuanto más densa se hace, más fuerte es este efecto, de manera que la contracción se vuelve cada vez más rápida. La velocidad de escape de la estrella, la velocidad con la que un objeto se debe mover para escapar del campo gravitacional, también aumenta. La métrica de Schwarzschild nos dice que, en alguna etapa, la velocidad de escape se hace igual a la de la luz. Ahora nada puede escapar, porque nada puede viajar más rápido que la luz. La estrella se ha convertido en un agujero negro, y el radio de Schwarzschild nos indica la región de la cual nada puede escapar, limitado por el horizonte de sucesos del agujero negro.

La física de los agujeros negros es compleja, y no hay espacio para hacerle justicia aquí. Basta con decir que la mayoría de los cosmólogos están ahora satisfechos con que la predicción es válida, que el universo contiene innumerables agujeros negros y, de hecho, que al menos uno merodea en el corazón de nuestra galaxia. En realidad, de la mayoría de las galaxias.

En 1917, Einstein aplicó sus ecuaciones a todo el universo, asumiendo otro tipo de simetría: homogeneidad. El universo debería tener el mismo aspecto (en una escala lo suficientemente grande) en todos los puntos en el espacio y el tiempo. Para entonces, había modificado las ecuaciones para incluir una «constante cosmológica» Λ, y averiguado el significado de la constante κ. Entonces escribió las ecuaciones así:

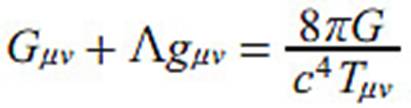
Las soluciones tuvieron una implicación sorprendente: el universo debería contraerse a medida que el tiempo pasase. Esto forzó a Einstein a añadir el término que involucra a la constante cosmológica; él estaba buscando un universo sin cambios y estable y al ajustar la constante al valor correcto, podía evitar el modelo de universo que se contrae hasta un punto. En 1922, Alexander Friedmann encontró otra ecuación, que predecía que el universo debería expandirse y no necesitaba una constante cosmológica. También predijo la velocidad de expansión. Einstein todavía no estaba contento, quería que el universo fuese estable e inmutable.

Por una vez, la imaginación de Einstein le falló. En 1929, los astrónomos americanos Edwin Hubble y Milton Humason encontraron pruebas de que el universo se está expandiendo. Galaxias distantes se están alejando de nosotros, como muestran los cambios en la frecuencia de la luz que emiten, el famoso efecto Doppler, en el cual el sonido de una ambulancia que va muy rápido disminuye cuando se aleja, porque las ondas de sonido se ven afectadas por la velocidad relativa del emisor y el receptor. Ahora las ondas son electromagnéticas y la física es relativista, pero hay todavía un efecto Doppler. No solo galaxias distantes se alejan de nosotros, sino que cuanto más distantes están, más rápido se alejan. Recorriendo la expansión hacia atrás en el tiempo, resulta que en algún punto en el pasado, todo el universo era esencialmente tan solo un punto.

Antes de eso, no existía en absoluto. En ese punto primigenio, tanto el espacio como el tiempo se originaron en el famoso Big Bang, una teoría propuesta por el matemático francés Georges Lemaître en 1927, y casi universalmente ignorado. Cuando los radiotelescopios observaron la radiación del fondo de las microondas cosmológicas en 1964, a una temperatura en la que se ajustaban al modelo del Big Bang, los cosmólogos decidieron que Lemaître había estado en lo correcto después de todo. De nuevo, el tema se merece un libro propio, y mucho se ha escrito. Basta decir que nuestra teoría actual aceptada mayoritariamente es una elaboración del escenario del Big Bang.

El conocimiento científico, sin embargo, es siempre provisional. Nuevos descubrimientos pueden cambiarlo. El Big Bang ha sido el paradigma cosmológico aceptado durante los últimos 30 años, pero está empezando a mostrar algunas fisuras. Varios descubrimientos o bien arrojan serias dudas sobre la teoría, o bien necesitan nuevas partículas y fuerzas físicas que han sido deducidas pero no observadas. Hay tres fuentes de dificultad principales. Las resumiré primero y luego discutiré cada una con más detalle. La primera son las curvas de rotación galáctica, que sugieren que la mayoría de la materia en el universo está perdida. La propuesta actual es que esto es un signo de un nuevo tipo de materia, materia oscura, que constituye alrededor del 90 % de la materia en el universo, y es diferente a cualquier materia ya observada directamente sobre la Tierra. La segunda es una aceleración en la expansión del universo, que necesita una nueva fuerza, energía oscura, de origen desconocido pero modelada usando la constante cosmológica de Einstein. La tercera es una colección de asuntos teóricos relacionados con la teoría popular de la inflación cósmica, que explica por qué el universo observable es tan uniforme. La teoría encaja con las observaciones, pero su lógica interna parece débil.

La materia oscura primero. En 1938, el efecto Doppler se usaba para medir la velocidad de las galaxias en grupo, y el resultado no era consistente con la gravitación newtoniana. Como las galaxias están separadas grandes distancias, el espacio-tiempo es casi plano y la gravedad newtoniana es un buen modelo. Fritz Zwicky sugirió que debe haber alguna materia no observada para explicar la discrepancia, y se llamó materia oscura porque no podía ser vista en fotografías. En 1959, usando el efecto Doppler para medir la velocidad de rotación de las estrellas en la galaxia M33, Louise Volders descubrió que la curva de rotación observada, un trazo de la velocidad respecto a la distancia al centro, era también inconsistente con la gravitación newtoniana, que de nuevo es un buen modelo. La velocidad en lugar de decaer en grandes distancias, permaneció casi constante (ver la siguiente figura). El mismo problema aparece para muchas otras galaxias.

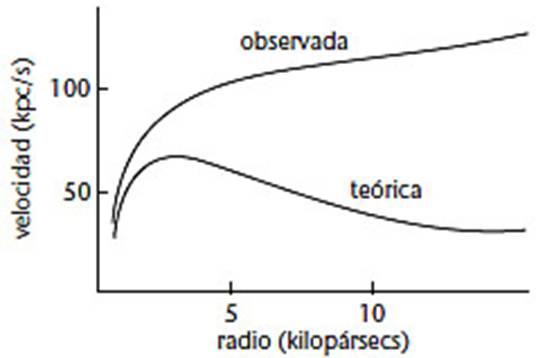
Curvas de rotación galácticas para M33: teoría y observaciones.

Si existe, la materia oscura debe ser diferente de la materia «bariónica» común, las partículas observadas en experimentos en la Tierra. Su existencia es aceptada por la mayoría de los cosmólogos, que argumentan que la materia oscura explica varias anomalías diferentes en las observaciones, no solo las curvas de rotación. Se han sugerido partículas candidatas, como WIMPs (de sus siglas en inglés weakly interacting massive particles, partículas masivas de interacción débil), pero hasta ahora estas partículas no se han detectado en experimentos. La distribución de la materia oscura alrededor de las galaxias se ha trazado asumiendo que la materia oscura existe y averiguando dónde tiene que estar para hacer las curvas de rotación planas. Generalmente parece formar dos esferas de proporciones galácticas, una sobre el plano de la galaxia y otra bajo él, como una mancuerna gigante. Esto es un poco como predecir la existencia de Neptuno a partir de discrepancias en la órbita de Urano, pero dichas predicciones requerían confirmación: hubo que encontrar a Neptuno.

La energía oscura se propone de modo similar para explicar los resultados de 1998 del High-Z Supernova Search Team, que esperaban encontrar pruebas que la expansión del universo se está haciendo más lenta a medida que se va perdiendo el impulso inicial del Big Bang. En su lugar, las observaciones indicaron que la expansión del universo está acelerándose, un hallazgo confirmado por el Supernova Cosmology Projects en 1999. Es como si alguna fuerza antigravedad dominase el espacio, empujando las galaxias lejos unas de otras a una velocidad cada vez mayor. Esta fuerza no es ninguna de las cuatro fuerzas básicas de la física: gravedad, electromagnetismo, fuerza nuclear fuerte, fuerza nuclear débil. Se llamó energía oscura. De nuevo, su existencia parece resolver otros problemas cosmológicos.

La inflación cósmica fue propuesta por el físico norteamericano Alan Guth en 1980 para explicar por qué el universo es extremadamente uniforme en sus propiedades físicas a escalas muy grandes. La teoría mostró que el Big Bang debería haber producido un universo que fuese mucho más curvo. Guth sugirió que un «campo inflatón» (no hay una errata, no es de inflación, está pensado para ser un campo cuántico escalar que se corresponda con una partícula hipotética, el inflatón) provocó que el primer universo se expandiese con una rapidez extrema. Entre 10^–36 y 10^–32 segundos después del Big Bang, el volumen del universo se multiplicó por el alucinante factor de 10⁷⁸. El campo inflatón no se ha observado (esto requeriría energías inviablemente altas), pero la inflación cósmica explica muchas características del universo, y encaja con las observaciones tan bien, que la mayoría de los cosmólogos están convencidos de que existe.

No es sorprendente que la materia oscura, la energía oscura y la inflación cósmica sean populares entre los cosmólogos, porque les permiten seguir usando sus modelos físicos favoritos, y los resultados están acorde con las observaciones. Pero las cosas están empezando a desmoronarse. Las distribuciones de la materia oscura no proporcionan una explicación satisfactoria de las curvas de rotación. Se necesitan cantidades enormes de materia oscura para mantener la curva de rotación plana fuera de las grandes distancias observadas. La materia oscura tiene que tener un momento angular tan grande que es poco realista, lo que es inconsistente con las teorías comunes de formación de la galaxia. La misma distribución inicial bastante especial de materia oscura se necesita en cada galaxia, lo cual parece improbable. La forma de mancuerna es inestable porque coloca la masa adicional en la parte externa de la galaxia.

A la energía oscura le va mejor, y está pensada para ser algún tipo de energía del vacío mecánico-cuántica, que surge a partir de fluctuaciones en el vacío. Sin embargo, los cálculos actuales del tamaño de la energía del vacío son del orden de 10¹²² veces más grande, lo que son malas noticias incluso por los estándares de la cosmología.

Los principales problemas que afectan a la inflación cósmica no son observaciones, ya que encaja con estas sorprendentemente bien, sino sus fundamentos lógicos. La mayoría de los escenarios de la inflación llevarían a un universo que difiere considerablemente del nuestro, lo que cuentan son las condiciones iniciales en el momento del Big Bang. Con el propósito de ajustarse a las observaciones, la inflación necesita que el estado temprano del universo sea muy especial. Sin embargo, hay también condiciones iniciales muy especiales que producen un universo justo como el nuestro sin invocar a la inflación cósmica. Aunque ambos conjuntos de condiciones son extremadamente raros, los cálculos realizados por Roger Penrose muestran que las condiciones iniciales que no necesitan la inflación cósmica superan en número a las que produce la inflación por un factor de un gúgolplex, diez elevado a 10 elevado a 100. De modo que explicar el actual estado del universo sin inflación cósmica sería mucho más convincente que explicarlo con ella.

Los cálculos de Penrose se apoyan en la termodinámica, que podría no ser un modelo apropiado, pero una aproximación alternativa, llevada a cabo por Gary Gibbons y Neil Turok, lleva a la misma conclusión. Esto es «desenrollar» el universo de vuelta a su estado inicial. Resulta que la mayoría de los estados iniciales potenciales no involucran un período de inflación, y aquellos que lo necesitan son una proporción extremadamente pequeña. Pero el mayor problema de todos es que cuando la inflación cósmica se casa con la mecánica cuántica, predice que las fluctuaciones cuánticas desencadenarán ocasionalmente la inflación cósmica en una pequeña región de un universo aparentemente estable. Aunque dichas fluctuaciones son raras, la inflación es tan rápida y tan enorme que el resultado neto son islas diminutas de espacio-tiempo normal rodeadas por regiones en constante crecimiento con inflación fuera de control. En esas regiones, las constantes fundamentales de la física pueden ser diferentes de sus valores en nuestro universo. De hecho, cualquier cosa es posible.

¿Puede una teoría que predice «cualquier cosa» ser probada científicamente? Hay alternativas, y se está empezando a analizarlas como si necesitasen ser tomadas en serio. La materia oscura podría no ser otro Neptuno, sino otro Vulcano, un intento de explicar una anomalía gravitacional invocando una materia nueva, cuando lo que realmente necesita cambiarse es la ley de la gravitación. La principal propuesta bien desarrollada es MOND, de las siglas en inglés de dinámica newtoniana modificada, modified Newtonian dynamics, propuesta por el físico israelí Mordehai Milgrom en 1983. Esto, de hecho, no modifica la ley de la gravedad, sino la segunda ley de movimiento de Newton. Asume que la aceleración no es proporcional a la fuerza cuando la aceleración es muy pequeña. Hay una tendencia entre los cosmólogos a asumir que las únicas teorías alternativas viables son la materia oscura o la MOND, de modo que si MOND no concuerda con las observaciones, eso deja sola a la materia oscura. Sin embargo, hay muchos modos potenciales de modificar la ley de la gravedad, y es improbable que encontremos el correcto de manera inmediata.

El fallecimiento de MOND se ha proclamado varias veces, pero en investigaciones adicionales no se ha encontrado un defecto decisivo todavía. El principal problema con MOND, a mi entender, es que pone en sus ecuaciones lo que espera obtener, es como Einstein modificando la ley de Newton para cambiar la fórmula cerca de una masa grande. En su lugar, encontró un modo radicalmente nuevo de pensar en la gravedad, la curvatura del espacio-tiempo. Incluso si mantenemos la relatividad general y su aproximación newtoniana, podría no haber necesidad de la energía oscura. En 2009, usando las matemáticas de ondas de choque, los matemáticos norteamericanos Joel Smoller y Blake Temple mostraron que hay soluciones para las ecuaciones del campo de Einstein en las que la métrica se expande a un ritmo que se va acelerando. Estas soluciones muestran que cambios pequeños en el modelo estándar podrían explicar la aceleración de galaxias observada sin invocar a la energía oscura.

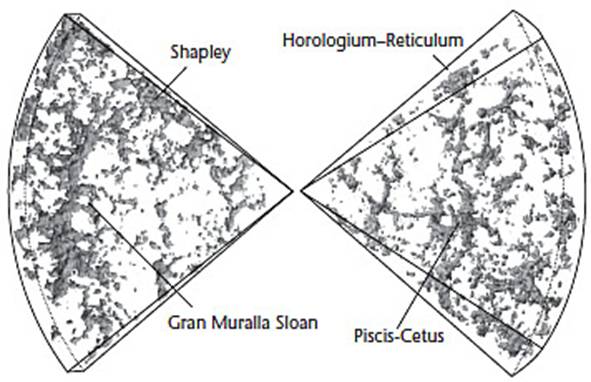
La rugosidad del universo

Los modelos del universo de relatividad general asumen que se forma una variedad, esto es, en escalas muy grandes la estructura se alisa. Sin embargo, la distribución de la materia observada en el universo a escalas muy grandes es a pedazos, como la Gran Muralla Sloan, un filamento compuesto de galaxias de 1.370 millones de años luz de largo (ver figura anterior).

Los cosmólogos creen que en escalas todavía mayores el alisamiendo se hará aparente, pero hasta la fecha, cada vez que el rango de observaciones se ha extendido, la forma rugosa ha persistido. Robert MacKay y Colin Rourke, dos matemáticos británicos, han argumentado que un universo rugoso en el cual hay muchas fuentes de gran curvatura locales podría explicar todos los misterios cosmológicos. Dicha estructura está más cercana a lo que se observa que cualquier alisamiento a gran escala y es consistente con el principio general de que el universo debería ser parecido en todas partes. En dicho universo no habría necesidad de ningún Big Bang, de hecho, todo podría estar en un estado estable y ser mucho, mucho, mucho más viejo que la cifra actual de 13.800 millones de años. Las galaxias individuales irían a través de un ciclo de vida, sobreviviendo relativamente invariables durante alrededor de 10¹⁶ años.

Tendrían un enorme agujero negro central. Las curvas de rotación galácticas serían planas debido al arrastre de la inercia, una consecuencia de la relatividad general en la que un cuerpo enorme que está rotando arrastra con él el espacio-tiempo alrededor de su entorno. El corrimiento al rojo observado en cuásares estaría provocado por un gran campo gravitacional, no por el efecto Doppler, y no sería indicativo de un universo en expansión. Esta teoría ha avanzado mucho gracias al astrónomo norteamericano Halton Arp, y nunca se ha refutado satisfactoriamente. El modelo alternativo incluso indica una temperatura de 5 K para el fondo de microondas cosmológicas, la principal evidencia (aparte del corrimiento al rojo interpretado como expansión) para el Big Bang.

MacKay y Rourke dicen que su propuesta «anula prácticamente todo principio de la cosmología actual. Sin embargo, no contradice cualquiera de las pruebas experimentales». Bien podría estar equivocada, pero el punto fascinante es que puedes mantener las ecuaciones del campo de Einstein sin cambios, prescindiendo de la materia oscura, la energía oscura y la inflación cósmica, y todavía obtiene un comportamiento razonable como todas esas observaciones misteriosas. De modo que cualquiera que sea el destino de la teoría, sugiere que los cosmólogos deberían considerar modelos matemáticos más imaginativos antes de recurrir a físicas nuevas aunque sin apoyo. La materia oscura, la energía oscura, la inflación, cada una de ellas necesita de físicas radicalmente nuevas que nadie ha observado... En ciencia, un “deus ex machina” genera escepticismo. Tres serían considerados intolerables en cualquier otra rama que no fuese la cosmología.

Para ser justos, es difícil hacer experimentos sobre todo el universo, de modo que teorías que encajen con las observaciones haciendo especulaciones son más o menos todo lo que puede hacerse. Pero imaginemos qué sucedería si un biólogo explicase la vida con algún «campo de vida» que no se puede observar, sin mencionar sugerir que un nuevo tipo de «material vital» y un nuevo tipo de «energía vital» fuesen también necesarias, mientras no proporciona pruebas de que alguna de ellas existe.

Dejando a un lado el reino desconcertante de la cosmología, ahora hay maneras más caseras de comprobar la relatividad, tanto la especial como la general, a una escala humana. La relatividad especial puede comprobarse en el laboratorio, y técnicas de medición modernas proporcionan una precisión exquisita. Aceleradores de partículas como el Gran Colisionador de Hadrones simplemente no funcionarían a menos que los diseñadores tuviesen la relatividad especial en cuenta, porque las partículas que dan vueltas en estas máquinas lo hacen a velocidades muy próximas a la de la luz. La mayoría de las pruebas de la relatividad general son todavía astronómicas, y van desde lentes gravitacionales a dinámica de púlsares, con un nivel de precisión alto. Un experimento reciente de la NASA en una órbita baja terrestre, usando giroscopios de alta precisión, confirmó la existencia del efecto de arrastre por inercia, pero fracasó en alcanzar la precisión deseada debido a unos efectos electrostáticos inesperados. Cuando se corrigieron los datos para este problema, otros experimentos ya habían logrado los mismos resultados.

Sin embargo, un ejemplo de dinámica relativista, tanto especial como general, está más cerca de nosotros: la navegación vía satélite de los coches. Los sistemas de navegación por satélite usados por conductores calculan la posición de los coches usando señales de una red de 24 satélites en órbita, el Sistema de Posicionamiento Global o GPS. El GPS es sorprendentemente preciso, y funciona porque la electrónica moderna puede manejar con seguridad y medir instantes de tiempo muy diminutos. Está basado en señales de tiempo muy precisas, pulsaciones emitidas por los satélites y recogidas en la tierra. Comparando las señales desde varios satélites se triangula la localización del receptor con un margen de error de unos pocos metros. Este nivel de precisión requiere saber el tiempo con un margen de error de 25 nanosegundos. La dinámica newtoniana no da localizaciones correctas, porque dos efectos que no se tienen en cuenta en las ecuaciones de Newton alteran el flujo del tiempo: el movimiento de los satélites y el campo gravitatorio de la Tierra.

La relatividad especial aborda el movimiento y predice que los relojes atómicos de los satélites deberían perder 7 microsegundos por día comparados con los relojes de la tierra, debido a la dilatación del tiempo relativista. La relatividad general predice una ganancia de 45 microsegundos por día provocados por la gravedad terrestre. El resultado neto es que los relojes en los satélites ganan 38 microsegundos por día debido a razones relativistas. Por pequeño que esto pueda parecer, su efecto en las señales de GPS no es de ninguna manera insignificante. Un error de 38 microsegundos es 38.000 nanosegundos, alrededor de 1.500 veces el error que el GPS puede tolerar. Si el software calculó la localización de un coche usando la dinámica newtoniana, esa navegación por satélite será inservible rápidamente, porque el error crecería a una velocidad de 10 kilómetros por día.

Si contamos 10 minutos a partir de ahora, el GPS newtoniano nos situaría en la calle equivocada, y mañana en la ciudad equivocada. En una semana estaríamos en la comunidad equivocada y en un mes en el país equivocado. Dentro de un año, estaríamos en el planeta equivocado. Si no crees en la relatividad, pero usas navegación por satélite para planear tus viajes, tienes un problema…y es relativo! 

© 2024 JAVIER DE LUCAS