UNIVERSO HOLOGRAFICO

UNIVERSO HOLOGRAFICO

Hace cerca de treinta años, la teoría de cuerdas dio lugar a su resultado más impactante: la conjetura de Maldacena. Según esta, la elusiva teoría cuántica de la gravedad podría tener una descripción relativamente simple en términos de lo que ocurre en la frontera del espacio-tiempo. ¿Puede ser el universo descrito como un holograma? Algunas razones respaldan esta idea.

Uno de los aspectos más interesantes de las D-branas es que expresan de manera alternativa las simetrías de dualidad que la teoría de cuerdas esconde en el seno de su formulación matemática Es decir: la existencia de dos maneras equivalentes, pero de apariencia radicalmente distinta, para describir un mismo fenómeno físico. El mejor ejemplo para ilustrarlo está en el propio proceso de interacción entre dos de dichos objetos extendidos.

Consideremos un par de D-branas que interactúan mediante el intercambio de cuerdas. En el diagrama de la izquierda de la figura 1 vemos cómo la fuerza que una D-brana ejerce sobre la otra está representada por el intercambio de una cuerda cerrada que se propaga libremente entre ambas. En el de la derecha, en cambio, la interpretación del proceso de interacción es diferente y responde a cuerdas abiertas que se propagan alrededor del cilindro imaginario que la cuerda cerrada habría dibujado en su andar. Ambas descripciones deben ser indistinguibles, como se intuye a partir de la figura. Son solo distintas formas de «recorrer» el mismo diagrama. A nivel del cálculo matemático, los resultados son exactamente iguales gracias a una asombrosa propiedad de la teoría, en particular, porque el diagrama de la izquierda involucra el intercambio de gravitones, mientras que estos brillan por su ausencia en el de la derecha.

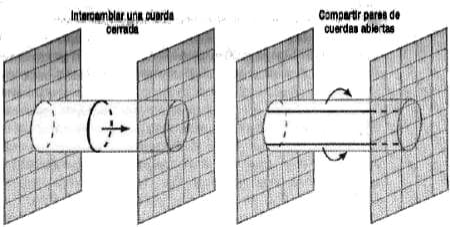
Figura 1. Dos D-branas que interactúan mediante el intercambio de cuerdas. La posibilidad de interpretar este proceso de más de una manera, como un intercambio de cuerdas cerradas (izquierda) o abiertas (derecha), obteniendo naturalmente el mismo resultado, expresa la simetría de dualidad de la teoría de cuerdas.

Esto induce a pensar que podría existir una formulación alternativa a la gravedad cuántica en la que, por así decirlo, no haya gravitones. La dualidad entre cuerdas cerradas y abiertas cuyos extremos se encuentran fijos sobre las D-branas es, también, otra muestra de la extraña manera en que las cuerdas «sienten» la estructura espacio-temporal, de una forma dual que nos permite recurrir a uno u otro modo de entender el mismo fenómeno, lo que representa una enorme ventaja de cálculo de la teoría.

La conjetura de Maldacena

Consideremos un conjunto de D3-branas paralelas. Para cada par de ellas es posible demostrar que el saldo neto de todas sus interacciones es cero, es decir, ni se atraen ni se repelen. Esto se debe a que la atracción gravitatoria entre las D3-branas se compensa con la repulsión debida a otros campos ante los cuales están cargadas. Por lo tanto, podemos alejarlas o acercarlas arbitrariamente, siempre respetando que se mantengan paralelas. Podemos tener varios tipos de cuerdas en esta situación. Dentro de las abiertas, estarán aquellas que tienen ambos extremos en una misma D3-brana, pero también habrá cuerdas que tienen caída extremo en distintas D3-branas (figura 2). Además, tendremos cuerdas cerradas que pueden viajar a través del espacio transverso, alejándose de todas las D3-branas a la vez. Las cuerdas abiertas pueden eventualmente cerrarse, si sus extremos se acercan hasta tocarse, desprendiéndose. De igual modo, el proceso inverso en el que una cuerda cerrada toca a una D3-brana y se engancha, separando sus extremos y convirtiéndose en una cuerda abierta, también es posible.

Estos procesos nos permiten deducir cuál es la teoría que describe este sistema de cuerdas y D-branas.

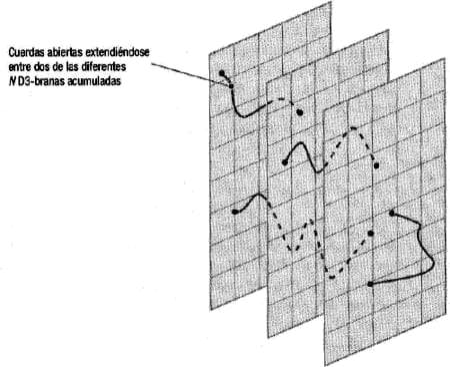
Figura 2. Conjunto de D3-branas paralelas en el que se muestran las distintas cuerdas abiertas.

En el nivel más bajo de energía, las oscilaciones de las cuerdas que tienen sus extremos en dos D3-branas distintas presentan, al estar inexorablemente estiradas, estados con una masa proporcional a su separación debido a la tensión de la cuerda. Podemos aumentar o disminuir dicha masa, alejando o acercando las DO-branas. Esto ya nos da una pista importante sobre el tipo de teoría que describe estas oscilaciones, ya que no son muchas las posibilidades disponibles en la caja de herramientas del físico teórico que sean compatibles con este extraño comportamiento. Las cuerdas abiertas con extremos en una misma D3-brana, en cambio, dan lugar a partículas sin masa, ya que pueden contraerse hasta tener tamaño cero. Por último, las cuerdas cerradas que completan esta configuración viajan libremente, por lo que se perciben como un espacio-tiempo plano 10-dimensional. Asimismo, las cuerdas abiertas y cerradas, en principio, interactúan entre ellas.

Imaginemos ahora que acercamos a todas las D3-branas (llamemos N al número de estas) hasta colocarlas arbitrariamente cerca las unas de las otras, es decir, en el mismo lugar del espacio. Son superficies geométricas sin grosor, por lo que esto es posible. Lo único que habrá cambiado significativamente es el comportamiento de aquellas partículas correspondientes a las vibraciones de las cuerdas que unían a D3-branas distintas, que pasarán ahora a tener masa cero por estar juntas. Esquemáticamente, podemos decir que la descripción de este sistema viene dada por la siguiente expresión:

S = S cuerdas abiertas en N D3-branas + S cuerdas cerradas lejanas + S interacción

donde la S quiere decir «Sistema». Esta ecuación es una forma esquemática de indicar lo que se describe en el párrafo que la precede. La teoría de cuerdas da cuenta de los tres términos de la expresión anterior, siendo el último el más complejo. Observemos ahora al sistema anterior desde un punto de vista distinto. Las D3-branas son hipersuperficies que tienen una tensión y, por lo tanto, una masa Su tamaño es infinito, de modo que la masa es todo menos pequeña. El conjunto de D3-branas, entonces, pueda ser visto como un cuerpo pesado que deforma al espacio-tiempo, como fruto de su enorme masa. Es posible, de hecho, utilizar las ecuaciones de Einstein para determinar la geometría (la curvatura del espacio-tiempo) que este sistema produce. La representación gráfica de lo que ocurre con el espacio-tiempo 10-dimensional es complicada, pero podemos simplificarla (figura 3).

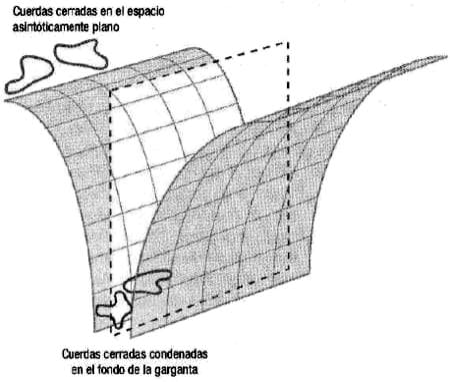
Figura 3. El conjunto de D3-branas deforma el tejido espacio-temporal debido a su masa. La dirección perpendicular representa, en realidad, a seis dimensiones espaciales. Así como podríamos imaginar un espacio tridimensional como el conjunto de todas las superficies esféricas posibles, podemos representar las seis direcciones transversas como el de todas las posibles esferas 5-dimensionales. Estas encierran N unidades de la «carga eléctrica generalizada» que poseen las D3-branas.

Allí se puede apreciar que el espacio-tiempo —representado como una superficie reticulada, sufre una marcada hendidura en el sitio en el que se encuentran superpuestas todas las D3-branas, pero con la particularidad de que lejos de ellas es plano, ya que allí su influencia gravitatoria es desdeñable. Cuando se estudia el campo gravitacional, también el electromagnético generalizado, producido por estos objetos, la forma correcta de hacerlo es, esquemáticamente, eliminar a las D3-branas (por eso las representamos con línea de trazos) y dejar en su lugar a los campos que generan. Así, al no tener D3-branas, nos encontramos ante un sistema de cuerdas cerradas que se mueven en presencia de la geometría y los campos electromagnéticos que aquellas provocaron. Al igual que las partículas elementales tienen la carga eléctrica cuantizada, lo que significa que solo puede tomar valores que sean múltiplos enteros de una carga mínima, la mecánica cuántica impone a las D3-branas una forma de carga que está repartida a lo largo de toda su extensión tridimensional, genera campos parecidos al electromagnético y también está cuantizada.

Así como pensamos que una carga eléctrica dada se debe a la presencia de cierta cantidad de electrones, diremos que la configuración de D3-branas tiene carga N, para indicar que su descripción microscópica está dada en términos de N D3-branas, cada una de las cuales tiene una unidad de la carga fundamental. Hay que recordar que existen seis direcciones transversas, debido a que el espacio-tiempo tiene diez dimensiones mientras que las D3-branas dibujan una estela de cuatro dimensiones al moverse en el tiempo, algo que no podemos representar en un papel. Así como podríamos concebir un espacio tridimensional como el conjunto de todas las superficies esféricas concéntricas posibles, podemos representar a las seis direcciones transversas como el conjunto de todas las posibles esferas 5-dimensionales. Estas encierran N unidades de la «carga eléctrica generalizada» que poseen las D3-branas; por analogía con el electromagnetismo se dice que las 5-esferas «encierran N unidades de flujo».

Es posible descomponer el sistema de un modo parecido al que utilizamos más arriba cuando lo analizamos desde el punto de vista en el que las D3-branas son hipersuperficies en las que acaban las cuerdas abiertas. Ahora se nos presenta una configuración que involucra solo cuerdas cerradas, pero en un espacio-tiempo curvo. Esquemáticamente, tenemos cuerdas cerradas que viven en el fondo de la hendidura (donde el campo gravitatorio es intenso), otras que lo hacen muy lejos de esta y, por último, está lo que llamaremos la interacción entre ambas, es decir, aquellas cuerdas que tienen posibilidades de salir o entrar en la hendidura:

S = S cuerdas cerradas en hendidura & N flujos + S cuerdas cerradas lejanas + S interacción

donde la S quiere decir, nuevamente, «Sistema». ¡Y se trata del mismo sistema que antes! Lo único que hemos hecho es interpretarlo de otro modo, analizándolo como lo haríamos con el Sol en el sistema solar, cuando toda su presencia se resume en el campo gravitatorio que genera y dicta el movimiento de los planetas. Si bien la interacción se refiere, en cada caso, a cuerdas distintas en situaciones muy diferentes, es posible caracterizar estos términos suficientemente como para damos cuenta de que, en el hipotético caso de que la longitud de la cuerda fuera arbitrariamente pequeña, estos dos términos también resultarían insignificantes. El cálculo que sustenta esta afirmación había sido realizado por Igor Klebanov, pero fue Juan Martín Maldacena quien se dio cuenta de las profundas consecuencias que esto conllevaba si se complementaba con una suposición adicional: que el número de D3-branas es enorme. Si consideramos que la longitud de la cuerda es muy pequeña, tomando la aproximación en la cual es infinitamente pequeña, los sistemas se parecen cada vez más a una de las antiguas teorías de partículas y campos, basadas en objetos puntuales. En esta aproximación, la energía de los estados oscilatorios de la cuerda se hace infinitamente grande y estos dejan de participar en la dinámica del sistema; en la cuerda de una guitarra, esto se vería en un aumento de la frecuencia al acortarla: en algún momento la nota resultante se hará tan aguda que saldrá de nuestro rango auditivo, sin importar cuán amplio sea.

En la descripción de cuerdas abiertas del sistema (véase la figura 2), considerar un tamaño de las cuerdas arbitrariamente pequeño lleva a una serie de simplificaciones en cada una de las tres partes en las que lo dividimos. La teoría de cuerdas da un resultado muy preciso para la dinámica de las cuerdas abiertas que tienen extremos en las N D3-branas. Se trata de una teoría muy concreta: la teoría n = 4 SYM, prima cercana de la que se utiliza en el modelo estándar. Es decir, la descripción de la dinámica de las D3-branas, en las condiciones discutidas más arriba, está dada, formalmente, por ¡el mismo tipo de teorías que describen la física de las partículas elementales!

Sin embargo, el prefijo n = 4 quiere decir que se trata de una extensión de la teoría de Yang-Mills con la máxima supersimetría posible. Esto nos aleja peligrosamente de la fenomenología: aún no se han encontrado indicios de supersimetría en los aceleradores más energéticos que hemos construido y lo que es seguro es que, de encontrarse, de ninguna manera habrá tanta.

La teoría n = 4 SYM es tan simétrica que incluso posee la simetría conforme que discutimos anteriormente, lo que conlleva una prohibición taxativa de la existencia de masa para las partículas. Esto constituye a priori un problema importante ya que, aunque «de la misma clase» que la QCD, la teoría n = 4 SYM parecería ser «demasiado simétrica» como para ser representativa de nuestro universo físico. Existen otras teorías cuánticas de campos con simetría conforme: a cada una de las cuales se la identifica con el apelativo de CFT (del inglés Conformal Field Theory). Aunque de momento no parezca esperanzadora, quizá sea oportuno recordar un aspecto de la teoría n = 4 SYM que ofrece un atractivo singular para los físicos teóricos: es única; no es posible construir ninguna otra con los mismos ingredientes. Tomemos esto como una motivación suficiente para seguir explorando lo que resulta del sistema de la figura 2. La contribución de las cuerdas cerradas lejanas se trivializa: con esto queremos decir que, si las cuerdas son pequeñas y el número de D3-branas es muy grande, se puede demostrar que dichas cuerdas no son más que gravitones que se pasean libremente por un espacio-tiempo plano.

Por último, y aquí aparece un aspecto clave del razonamiento que lleva a la conjetura de Maldacena, las interacciones, el tercer y más complejo elemento del sistema, se ven totalmente suprimidas.

El espacio-tiempo anti-de Sitter

El espacio Anti-de Sitter (AdS) es un tipo de geometría que no le resultará familiar al lector. Aunque se puede formular de manera matemática precisa y consistente sobre el papel, sus propiedades se alejan mucho de la geometría euclídea a la que estamos acostumbrados. Basta con decir que en el espacio AdS, infinito como podría serlo el espacio cartesiano, un rayo de luz puede llegar al infinito y, si se dispusiera allí un espejo, retornar al cabo de un lapso de tiempo. Si en lugar de un rayo de luz lanzáramos una piedra, esta también regresaría al cabo del mismo tiempo, como si se tratara de un bumerán, pero sin haber logrado alcanzar el infinito, ya que eso le demandaría una energía ilimitada. En el espacio AdS se pueden trazar infinitas paralelas a una recta que pasen por un punto ajeno a ella, algo que es imposible de lograr sobre el papel.

Podemos sintetizar lo discutido hasta aquí indicando que, si suponemos que la longitud de la cuerda es arbitrariamente pequeña y el número de D3-branas muy grande, el sistema de la figura 2, se ve simplificado a:

S n = 4 SYM + S gravitones libres

Es interesante explorar lo que ocurre con la descripción de cuerdas cerradas del sistema cuando consideramos el mismo límite. Recordemos que estas se mueven en una geometría muy concreta que se muestra esquemáticamente en la figura 3. En este caso es bastante más sencillo indicar lo que ocurre: el límite estrecha la hendidura y la hace muy profunda Como resultado, las pequeñas cuerdas cerradas quedan atrapadas en el fondo y la probabilidad de que una de ellas emerja de la hendidura es nula, lo mismo que aquella que contabiliza la posibilidad de que una cuerda cerrada que está fuera se interne en una hendidura en la que, para decirlo coloquialmente, no cabe. Esto quiere decir que el último término, el término de interacción, desaparece completamente. El primer término describe a las pequeñas cuerdas cerradas que se mueven en una hendidura profunda, la cual adopta una forma muy precisa: la geometría resultante se conoce como «espacio Anti-de Sitter (AdS) en cinco dimensiones».

En realidad, el espacio-tiempo tiene, como ya sabemos, diez dimensiones, pero en este caso ocurre una simplificación afortunada: las otras cinco dimensiones constituyen una sencilla esfera (¡cinco-dimensional!). Esta esfera dejará huellas en la física del sistema y es depositaría de una pieza relevante de información. Recordemos que la configuración estaba caracterizada por un número natural, N, que indicaba el número de D3-branas y que, según la aproximación propuesta por Maldacena, es muy grande. Pues bien, este número persiste en las N unidades de carga encerradas por la 5-esfera.

Por último, las pequeñas cuerdas cerradas lejanas ven una geometría plana, ya que toda la curvatura se ciñe a la pequeña región en la que se extiende la hendidura. De modo que, con estas simplificaciones, el sistema resulta

S = S gravedad en AdS & N flujos + S gravitones libres

donde es importante remarcar que el primer término corresponde a una teoría de gravedad supersimétrica muy concreta llamada Tipo IIB, que se obtiene de la teoría de cuerdas homónima en el régimen de bajas energías. Pero estos dos sistemas, a pesar del distinto aspecto que presentan, ¡son el mismo! Son dos descripciones alternativas de un mismo conjunto de N D3-branas planas. Por tanto, podemos igualar las dos últimas expresiones de S y, tras cancelar el segundo sumando del miembro derecho, que en ambos casos corresponde a pequeñas cuerdas cerradas libres en un espacio-tiempo plano, llegamos a la sorprendente igualdad

S gravedad en AdS & N flujos = S n = 4 SYM

a la que llamaremos, críptica pero significativamente,

AdS = CFT

Esta maravillosa ecuación, conocida como la conjetura de Maldacena, cuyas consecuencias explicaremos a continuación, es una de las más extraordinarias que se hayan escrito jamás. AdS es una forma económica de escribir «Supergravedad Tipo IIB en AdS5 × S5 con N unidades de flujo». Esta es una teoría cuántica por construcción —más estrictamente, lo es la teoría de cuerdas tipo IIB: la supergravedad aparece aquí porque estamos trabajando en el límite de cuerdas muy pequeñas y N es un número arbitrariamente grande. Haber conseguido una ecuación en la que en uno de los lados del signo igual se halla una teoría cuántica de la gravedad es un hito extraordinario; un objetivo perseguido durante nueve décadas. Nadie había imaginado, ¡eso sí!, el exotismo de lo que estaría al otro lado del signo igual, algo tan distinto en apariencia: una teoría cuántica de campos con simetría conforme ¡en una dimensión menos! Esto último, el hecho de que la gravedad cuántica pueda describirse haciendo uso de menos dimensiones espaciales, es lo que le da carta de naturaleza holográfica a la también denominada correspondencia AdS/CFT. Desde la aparición de la conjetura de Maldacena, el 27 de noviembre de 1997, los trabajos que la han estudiado, puesto a prueba, generalizado y, en general, investigado, se cuentan por miles.

Describiremos algunos resultados obtenidos a partir de esta conjetura y su rol en el contexto de la teoría de cuerdas.

Una nueva mirada sobre una vieja imagen

La conjetura de Maldacena proporcionó una nueva mirada sobre antiguos problemas que se remontan a la mismísima génesis de la teoría de cuerdas. Las investigaciones basadas en las ideas fundacionales de Veneziano presuponían implícitamente que las cuerdas eran las responsables de mantener juntos a los quarks; más específicamente, al par quark-antiquark que constituye un mesón. La propia QCD explica que el confinamiento de los quarks es mediado por una suerte de campo electromagnético generalizado: el campo fuerte, cuyas líneas de fuerza, a diferencia de lo que ocurre con las del electromagnetismo, que se esparcen como las púas de un erizo, como podemos comprobar con un imán y un puñado de limaduras de hierro, se concentran como si formaran un cordón deshilachado que mantiene juntos a los quarks.

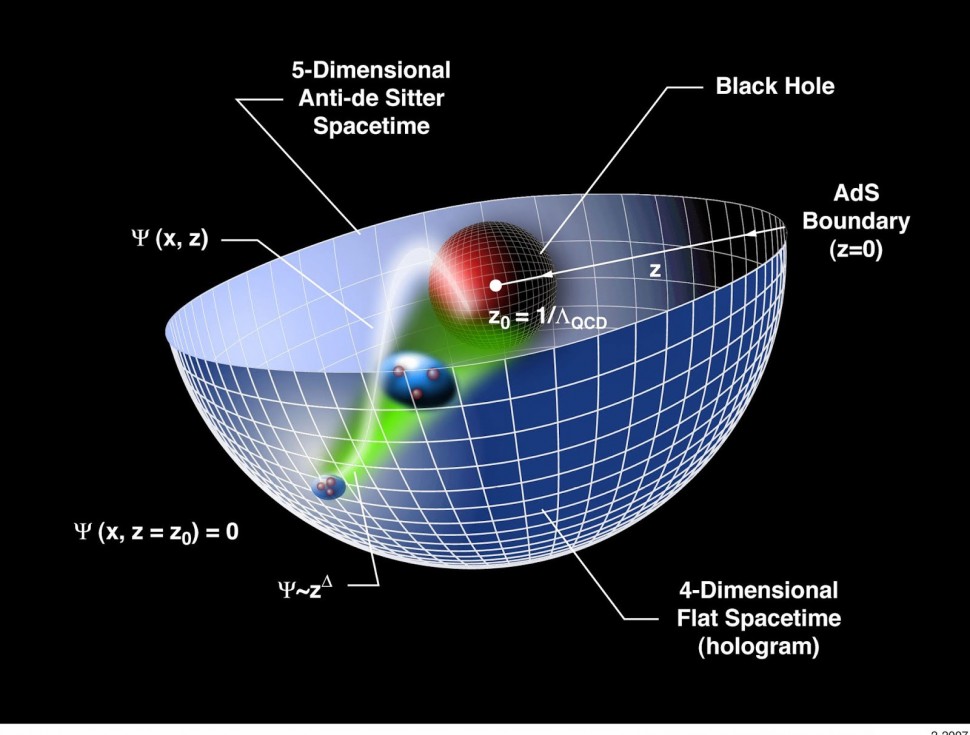
Durante mucho tiempo se pensó que, de alguna manera aún por determinar, ese cordón era el objeto descrito por la teoría de cuerdas. Sin embargo, el hecho de que tuviera un ancho característico, una escala de longitud asociada, contradecía al espesor nulo de la cuerda fundamental. La existencia de una quinta dimensión holográfica, es decir, que es perpendicular a las dimensiones de la teoría CFT, da cumplida respuesta a este punto. Una cuerda sin espesor que se adentra en la quinta dimensión llegando hasta un punto y regresando a la frontera adquiere necesariamente una escala: la que le proporciona la profundidad de penetración (figura 4). El grosor del cordón que mantiene unidos al quark y al antiquark es, por así decirlo, la «sombra holográfica» de esa profundidad.

El lector seguramente se siente en este punto escéptico y desconcertado por la existencia de la dimensión holográfica. Sin embargo, cederá más fácilmente si se presenta el resultado de Maldacena desde otro punto de vista.

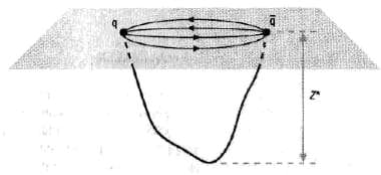
Figura 4. Un quark y un antiquark que, unidos, forman un mesón (un ejemplo conocido son los piones que se generan en la atmósfera debido a los rayos cósmicos). Según la teoría QCD, el par quark-antiquark se mantiene unido debido a los gluones que dan entidad a las líneas de campo fuerte, representadas aquí por las flechas. Debido a la presencia de la dimensión holográfica, los gluones aparecen como «sombras platónicas» de una cuerda fundamental que se extiende en esa dimensión extra y a la que los quarks y antiquarks, extremos de la cuerda, no pueden acceder. El ancho del cordón fuerte viene dictado por la profundidad de penetración en la dimensión holográfica, Z*.

Así como se puede argumentar que Einstein extendió las dimensiones del universo de tres a cuatro al incorporar al tiempo, pasando del espacio al espacio-tiempo, podríamos afirmar que Maldacena descubrió que, a nivel cuántico, la energía se incorpora de una manera muy especial al espacio-tiempo para dar lugar a un ente 5-dimensional en el que las ecuaciones de la física son más sencillas y adoptan un «sentido superador». Con esto queremos decir lo siguiente: Uno podría insistir en mantener separado al espacio del tiempo en la teoría de la relatividad y formular en ese escenario las ecuaciones. Esto es, desde luego, posible. Lo único que conseguiríamos en tal caso sería un formalismo en apariencia más complejo y, desde luego, bastante menos elegante. Decidir incluir al tiempo junto a las dimensiones del espacio, al margen de sus implicaciones conceptuales, se puede pensar como una opción adecuada para que la teoría adopte una forma más simple. Pero una vez que se realiza esta inclusión, la noción de espacio-tiempo funciona como una puerta abierta a nuevas ideas, superadoras, que eran difícilmente apreciables con el formalismo anterior. El salto conceptual puede pensarse como el regocijando clic que hacen dos piezas al encajar perfectamente.

Lo mismo puede decirse de la inclusión de la «dimensión energía». Aunque no estemos obligados a hacerlo, si la incorporamos a las del espacio-tiempo en una teoría y nos adentramos en el régimen no-perturbativo de esta, comprobaremos que el espacio-tiempo-energía adquiere un nuevo sentido, superador. Lo que nos dice la conjetura de Maldacena es que la física de un sistema semejante «debe» ser pensada en términos completamente distintos. De alguna manera, la lección es que las descripciones de los fenómenos físicos, tales como la gravedad o las interacciones nucleares, en distintos regímenes pueden venir dadas por representaciones espacio-temporales muy diferentes. Mientras que en numerosas ocasiones la descripción adecuada de un fenómeno parece ser la brindada por un espacio-tiempo 4-dimensional como el que se considera en la física de partículas, en otras nos encontramos con fenómenos, acaso correspondientes a la misma fuerza poro en un régimen distinto, cuya descripción resulta más iluminadora en términos de una teoría en un espacio-tiempo 5-dimensional, o 10-dimensional.

Así, la idea de dimensionalidad como un absoluto se desdibuja y, con ella, la imagen que hasta el momento teníamos de aquello que llamamos espacio-tiempo.

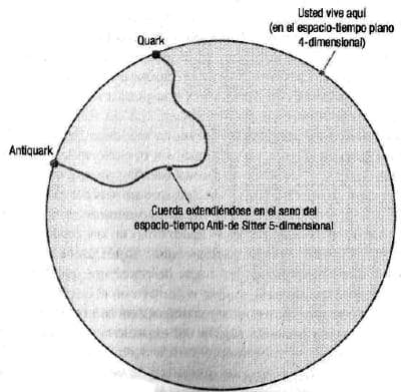
Figura 5. Representación esquemática del universo holográfico de la conjetura de Maldacena. En el interior del círculo hay una teoría cuántica de la gravedad, cuya descripción holográfica reside en la circunferencia que define la frontera. Alternativamente, si ponemos el foco en la frontera, cuando la teoría que vive allí está en el régimen no-perturbativo, su descripción más apropiada está dada en términos de una teoría de gravedad ordinaria que vive en el Interior del espacio-tiempo 5-dimensional.

Un fenómeno como la interacción nuclear puede ser 4-dimensional en un régimen (cuando los quarks se mueven muy rápido unos respecto a los otros), mientras que deviene 10-dimensional en el régimen opuesto (cuando los quarks se encuentran cerca y se mueven solidarios unos con los otros). Una representación gráfica que permite entender mejor la naturaleza holográfica de la conjetura de Maldacena es la que brinda la figura 5. En ella no se incluye la 5-esfera y, a efectos de que se pueda representar en las dos dimensiones del papel, solo se muestra la dimensión holográfica (la dirección radial del círculo) y una de las cuatro que nuestra realidad sensorial percibe (la dirección angular).

Podemos pensar que la física fundamentad, la química y la biología, acontecen en el borde del círculo, que, insistimos, es 4-dimensional, mientras que la dirección radial que nos lleva a su interior solo puede ser explorada por cuerdas con extremos en el borde, tal como aquellas responsables de mantener a la pareja quark-antiquark en el interior de los mesones, como se muestra en la figura, o por cuerdas cerradas que se aventuran hacia el interior de la geometría. El uso fenomenológico de la conjetura de Maldacena ha proporcionado algunos resultados interesantes. Mencionaremos solo uno, a manera de ejemplo. Si bien las teorías n = 4 SYM y QCD encierran diferencias cualitativas, ambas se asemejan notablemente cuando entra en juego la temperatura. El ejemplo paradigmático de un sistema conformado por quarks y gluones a alta temperatura es el denominado «plasma de quarks y gluones», un estado de la materia que pudo ser generado experimentalmente en el año 2000 mediante la colisión muy energética de iones pesados (oro, en el caso del experimento estadounidense RHIC (Relativistic Heavy Ion Collider, ubicado en el Laboratorio Nacional de Brookhaven, en Upton, Nueva York), y plomo, en el más reciente experimento europeo, Alice, que se realiza utilizando las instalaciones del LHC). En estos experimentos se hacen chocar los núcleos de frente —cada uno de los cuales tiene unos 200 nucleones en su interior— que viajan prácticamente a la velocidad de la luz; así, en lugar de tener una colisión nucleón-nucleón, se tiene un choque colectivo en el que la energía depositada por los numerosos participantes es mucho mayor. Esto produce una pequeña región del espacio con forma de almendra, la razón es meramente geométrica (figura 6), en la que la temperatura resulta casi un millón de veces la del núcleo del Sol; la misma que tuvo el universo cuando su edad rondaba la millonésima de segundo.

Semejante «caldera» pone a disposición de cada uno de los quarks y gluones que se encuentran allí una enorme cantidad de energía. La teoría QCD dictamina que los quarks y gluones se comportan como si estuvieran libres de toda interacción a energías «suficientemente» altas. La expectativa, pues, era observar en estos experimentos algo parecido a un plasma gaseoso de quarks y gluones que, tras la colisión, salieran despedidos en todas las direcciones por igual: si su interacción es nula o muy pequeña, cada partícula saldría en alguna dirección aleatoria, independiente de las demás, por lo que los detectores no registrarían indicios de la asimetría geométrica de la región de interacción desde la que partieron.

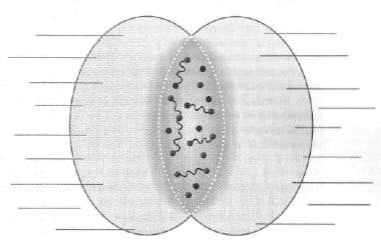
Figura 6. Dos núcleos pesados que colisionan a muy altas energías (su forma se distorsiona por el fenómeno de contracción relativista a lo largo de la dirección del movimiento), lo hacen en una reglón con forma de almendra en la que se deposita la energía de la colisión. Los resultados experimentales indican que la colección de quarks y gluones en esa región, a muy alta temperatura, se comporta como un fluido de muy baja viscosidad.

Lo que se observa en los experimentos dista mucho de esto. La asimetría persiste en los detectores, como si el plasma de quarks y gluones fuera más bien un líquido fuertemente interactuante y ¡de bajísima viscosidad! Al mismo tiempo que los físicos de partícula» encontraban grandes dificultados para reproducir desde la teoría este extraño e inesperado comportamiento de la materia, Giuseppe Policastro, Dam Thanh Son y Andrei Starinets hicieron uso de la conjetura de Maldacena para acometerlo, amparados en el hecho de que a altas temperaturas las teorías n = 4 SYM y QCD tienen unos cuantos parecidos, y el régimen no-perturbativo del problema justifica abordarlo dejando por un momento nuestro universo 4-dimensional para sumergirnos en la quinta dimensión holográfica.

El valor que obtuvieron para la viscosidad era compatible con los resultados experimentales, y más tarde se demostró que tenía cierto grado de universalidad. En la misma línea, la conjetura de Maldacena ha sido utilizada también con éxito razonable paira describir otros sistemas fuertemente acoplados (es decir, en el régimen no-perturbativo); por ejemplo, en física del estado sólido o en sistemas de átomos fríos. Ha servido también para realizar valiosos aportes al cálculo de la entropía de entrelazamiento de diversos sistemas, cantidad relevante en el dominio de la llamada teoría de la información cuántica. Alcanza con señalar aquí, como frívolo pero contundente indicador de su relevancia y potencial, que el trabajo original de Maldacena es el más citado del que se tenga registro en la historia de la física de las interacciones fundamentales.

Hacia una teoría cuántica de la gravitación

Pero la conjetura de Maldacena también sirve para describir los diferentes regímenes (incluyendo el cuántico) de la fuerza gravitatoria. En este sentido, sus aplicaciones a la teoría de los quarks podrían clasificarse como las de una poderosa herramienta conceptual y de cálculo, pero casi irrelevantes frente a la presunción de ser la portadora del primer marco teórico explícito en el que conviven la teoría de la relatividad general y la mecánica cuántica. Una de las consecuencia» casi inmediatas de la conjetura de Maldacena en el contexto de la interacción gravitacional tiene que ver con la paradoja de la información de los agujeros negros, formulada hace cuarenta años por Stephen Hawking. Si la dinámica cuántica de un agujero negro (al menos en un espacio-tiempo Anti-de Sitter) está descrita holográficamente por una teoría ordinaria en la frontera del espacio, tal como la ecuación AdS = CFT sugiere, y dado que la segunda de estas teorías se sabe perfectamente «unitaria», es decir, que preserva la cantidad de información, entonces también la primera deberá serlo. El proceso de evaporación de los agujeros negros, inexorablemente, deberá corresponder a un proceso unitario: lo que equivale a decir que la información atrapada en esos astros no se pierde sino que, de alguna manera abstrusa y no del todo comprendida, es preservada.

El truco de recurrir a la descripción dual en la frontera y responder así a interrogantes que necesariamente conducen a la naturaleza cuántica que el espacio-tiempo alberga a escalas microscópicas —como la termodinámica de los agujeros negros— se ha convertido en una herramienta estándar. Nunca antes se dispuso de una propuesta tan concreta para una teoría cuántica de la gravedad. Tampoco se contaba con la posibilidad de utilizarla para poner a prueba aquellos aspectos conceptuales que resultan confusos. La conjetura de Maldacena se ha convertido en una disciplina en sí misma. Su propio estatus conjetural hace que, por así decirlo, no esté totalmente claro cuál es su alcance. En los años recientes se ha ensayado extender el dominio de esta técnica a los más diversos rincones de la física, desde los sistemas de materia condensada similares a los que controlamos en los laboratorios hasta la cosmología del universo temprano, desde la superconductividad hasta el universo inflacionario.

Los más conservadores podrían pensar que, de ser correcta, la conjetura solo se aplicaría al ejemplo brindado por las D3-branas que obtuvo inicialmente Maldacena. Sin embargo, dado que en ese ejemplo lo que subyace es la dualidad entre cuerdas abiertas y cerradas para describir un mismo sistema, parece razonable extender el rango de validez a cualquier conjunto de Dp-branas. Esto es mucho más importante que un mero ejercicio académico, ya que es posible reproducir una fenomenología compatible con la de nuestro universo 4-dimensional utilizando configuraciones de Dp-branas de diversa dimensionalidad, a través de sus intersecciones y compactificaciones en las dimensiones extra, por ejemplo, una D5-brana enrollada en una esfera pequeña luce como una teoría en cuatro dimensiones a escalas mayores que el radio de la esfera. Con estos escenarios se puede dar cuenta del modelo estándar y se desprenden genéricamente algunas consecuencias interesantes como la existencia de partículas de mayor masa que podrían ser encontradas en el LHC próximamente.

¿Qué lugar ocupará la teoría de cuerdas dentro de un siglo? Pocas dudas caben que en las matemáticas persistirá su importancia e interés, habiéndose garantizado con numerosos resultados en campos como la topología y la geometría un sitio permanente en su bibliografía. En física la respuesta es algo más incierta. Michael Atiyaih, uno de los matemáticos más importantes del siglo XX y cuyo trabajo se desarrolló siempre en la frontera entre ambas disciplinas, dice que «los matemáticos somos como los abogados: nuestro cliente puede ganar o perder, nosotros siempre ganamos». Pero en una ciencia natural como la física no hay garantías. Es cierto que los más grandes físicos de finales del siglo XIX, incluyendo al padre de la teoría electromagnética, James Clerk Maxwell, dedicaron parte de su vida a entender la compleja dinámica del éter, para que pocos años después se demostrara su inexistencia y todo su formidable trabajo quedara en el olvido. Pero no lo es menos que las ideas de los sabios griegos Leucipo y Demócrito, tras quedar sepultadas por casi dos mil años, fueron reivindicadas por la ciencia. Hoy es imposible predecir si la teoría de cuerdas tendrá el destino del éter o del átomo. Sabrá comprender el lector que alberguemos una tímida y secreta esperanza de que acontezca lo segundo.

Se puede ponderar una teoría por las respuestas que brinda pero también por la calidad de los interrogantes que abre. Muchas de las preguntas que generó la teoría de cuerdas eran inimaginables antes de su formulación e impregnaron de valiosas ideas a las más diversas áreas de la física teórica. Si tuviéramos la certeza absoluta acerca de los caminos que debemos seguir para explorar lo desconocido, si la física no fuera un puzle de solución incierta, no lo llamaríamos investigación.